思路: 题目本身很简单,就是讲N划分为K个数的和有几种划分(1.....K)对应每一个K有 C(N-1,K-1)中划分法,一共就是 2^(N-1)。
但是发现N最多为 10^100000 哪怕快速幂也会爆.
方法1: 这也是我自己的一个做法吧,因为取模了,可以用欧拉降幂公式.
PS : 1e9+7 是大素数,所以他的欧拉函数值为1e9+6(根本不需要跑欧拉,可以直接得出),相比N的值已经小了很多了.跑一次快速幂就好. 而且并不要求a和n互质!!!!!
复杂度 O(log(1e9+6)).当 b<φ(n)时,b很小,直接快速幂即可,
简单介绍一些欧拉函数:
φ(n)定义为不超过n且与n互质的正整数的个数. 如:φ(3) = φ(6)=2等。
1. 欧拉函数的性质
p是n的质因子,那么有: φ(i*n*p)= φ(i*n)*p
推论: 当n为奇数时,φ(2*n) = φ(n)
2. 欧拉函数的三种求法 :
(1) 枚举 不超过n的数,暴力判断 复杂度 nlogn
(2) 利用欧拉求值公式: 复杂度 sqrt(n)
(3) 欧拉筛 O(n) 筛出1~n φ(n) ,O(1)查询.
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<set>
#include<vector>
#include<queue>
#include<map>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
const ll mod=1e9+7;
char s[maxn];
/*
ll phi(ll n)
{
ll res=n,a=n;
for(int i=2;i*i<=n;i++)
{
if(a%i==0)
{
res-=res/i;
while(a%i==0) a/=i;
}
}
if(a>1)
res-=res/a;
return res;
}*/
ll qmod(ll x,ll y)
{
ll res=1;
while(y)
{
if(y&1)
res=res*x%mod;
x=x*x%mod;
y>>=1;
}
return res;
}
int main()
{
//ll phim=phi(mod);
ll phim=1000000006;
//printf("%lld\n",phim);
while(~scanf("%s",s))
{
ll res=0;
int len=strlen(s),i;
for(int i=0;i<len;i++)
{
res=res*10+s[i]-'0';
if(res>mod)
break;
}
if(i==len)
printf("%lld\n",qmod(2,res-1));
else
{
res=0;
for(int i=0;i<len;i++)
{
res=res*10+s[i]-'0';
res%=phim;
}
printf("%lld\n",qmod(2,res-1+phim));
}
}
return 0;
}
网上还有大牛用费马小定理做的,我也来学习一发.
费马小定理:
特别的,当p为素数时,x无法被p整除,φ(p)=p-1,于是便有费马小定理Xp-1≡1(mod p)
在p是素数时,对任意正整数x都有Xp≡X(mod p)
那么对于这个题目,我们可以将2 ^(n -1 ) 的(n - 1 )拆成 k*(p-1)+t ,对于 2^(k*(p-1)) 根据费马小定理得到的答案为1,相乘对结果无影响,所以只需计算 2^t 即可. 这样也就保证了把 指数控制在了p范围内,是一个非常强的想法.
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
const int maxn=1e5+10;
char str[maxn];
ll qmod(ll x,ll y)
{
ll res=1;
while(y)
{
if(y&1)
res=res*x%mod;
x=x*x%mod;
y>>=1;
}
return res;
}
ll xiaofeima(ll m)
{
int len = strlen(str);
ll res = 0;
for(int i = 0; i < len ; i++)
{
res = res * 10 + str[i] - '0';
res %= m;
}
res = (res + m - 1) % m;//这里我是先拆的n,所以最后结果要-1,但是要取模.
ll ans = qmod(2,res);
return ans;
}
int main(){
while(~scanf("%s",str))
{
ll ans = xiaofeima(mod - 1);
printf("%lld\n",ans);
}
return 0;
}
Given A,B,C, You should quickly calculate the result of A^B mod C.
(1<=A,C<=1000000000,1<=B<=10^1000000).
这个题和上面那个就一样了,裸的欧拉降幂.因为这里C不一定是质数,所以无法使用费马小定理,而欧拉降幂公式对A 和C 是否互质未作要求
因为这里就求一次,所以直接用O(sqrt(n))的欧拉求值函数公式求一次即可.
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
ll a,c;
char b[maxn];
ll phi(ll n)
{
ll res=n,tmp=n;
for(int i=2;i*i<=n;i++)
{
if(tmp%i==0)
{
res-=res/i;
while(tmp%i==0)
tmp/=i;
}
}
if(tmp>1)
res-=res/tmp;
return res;
}
ll qmod(ll x,ll y)
{
x%=c;
ll res=1;
while(y)
{
if(y&1)
res=res*x%c;
x=x*x%c;
y>>=1;
}
return res;
}
int main()
{
while(~scanf("%lld %s %lld",&a,b,&c))
{
ll res=0;
ll phic=phi(c);
int len=strlen(b),i;
for(i=0;i<len;i++)
{
res=res*10+b[i]-'0';
if(res>phic)
break;
}
if(i==len)
{
printf("%lld\n",qmod(a,res));
}
else
{
res=0;
for(i=0;i<len;i++)
{
res=(res*10+b[i]-'0')%phic;
}
printf("%lld\n",qmod(a,res+phic));
}
}
return 0;
}
根据上面这个式子可以发现我们每进行一次欧拉降幂,就可以减少一个2,而且mod的p,将一次幂变成了φ(p).那么就肯定有一个时刻φ(p) 为1 ,那么 任何一个数%1=0,则f(p)=1.这个过程可以递归来做即可.
PS :这个题目的话你其实直接对于每个p去求欧拉函数,比全部筛出来要快... 复杂度为 O(T*sqrt(n)*logn)。
欧拉筛的话复杂度 O(p+T*logp)。可能因为p太小?
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<set>
#include<vector>
#include<queue>
#include<map>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int maxn=1e7+10;
vector<int>prime;
int phi[maxn];
//欧拉筛模板
void init()
{
phi[1]=1;
for(int i=2;i<maxn;i++)
{
if(phi[i]==0)
{
prime.push_back(i);
phi[i]=i-1;
}
for(int j=0;j<prime.size()&&prime[j]*i<maxn;j++)
{
if(i%prime[j]==0)//关键
{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else
//phi[i*prime[j]]=phi[i]*phi[prime[j]];
phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
}
ll qmod(ll x,ll y,ll mod)
{
ll res=1;
while(y)
{
if(y&1)
res=res*x%mod;
x=x*x%mod;
y>>=1;
}
return res;
}
ll solve(ll p)
{
if(p==1ll) return 0;
return qmod(2,(ll)solve((ll)phi[p])+(ll)phi[p],p);
}
int main()
{
init();
int t;
scanf("%d",&t);
while(t--)
{
ll p;
scanf("%lld",&p);
printf("%lld\n",solve(p));
}
return 0;
}
#include <map>
#include <cstdio>
using namespace std;
map<int, int> f;
int pow(int x, int k, int p)
{
int ret = 1;
while(k)
{
if(k & 1)
ret = (long long)ret * x % p;
x = (long long)x * x % p;
k >>= 1;
}
return ret;
}
int phi(int x)
{
int ret = x;
for(int i = 2; i * i <= x; ++i)
if(x % i == 0)
{
ret -= ret / i;
while(x % i == 0)
x /= i;
}
if(x > 1)
ret -= ret / x;
return ret;
}
int F(int x)
{
if(f.count(x))
return f[x];
int p = phi(x);
return f[x] = pow(2, F(p) + p, x);
}
int main()
{
int t, n;
scanf("%d", &t);
f[1] = 0;
while(t--)
{
scanf("%d", &n);
printf("%d\n", F(n));
}
return 0;
}
题意:
有一个n*n的二维格点,问在原点(0,0)处能看到多少个格点?(n<=1000,1000组数据)
思路:
我们可以发现什么样的点才是能看到的呢?对于一个点(x,y) ,他可以在原点被看到当且仅当 gcd(x,y) == 1
其次我们可以发现,所能看到的点是关于对角线对称的,所以我们可以只算一个上三角然后对称一下即可.
我们可以固定纵坐标,寻找横坐标,那么横坐标的所有可能就是 纵坐标 y的φ(y)。然后y从2~n 求和即可.
PS : y轴和x轴还有对角线的在我们计算过程中没算进去,要加上
一个欧拉筛即可.
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<set>
#include<vector>
#include<queue>
#include<map>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int maxn=1e3+10;
vector<int>prime;
int phi[maxn];
void init()
{
phi[1]=1;
for(int i=2;i<maxn;i++)
{
if(phi[i]==0)
{
prime.push_back(i);
phi[i]=i-1;
}
for(int j=0;j<prime.size()&&prime[j]*i<maxn;j++)
{
if(i%prime[j]==0)
{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else
phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
}
int main()
{
int t;
cin>>t;
init();
int ca=1;
int n;
while(t--)
{
scanf("%d",&n);
ll ans=3;
for(int i=2;i<=n;i++)
ans+=2*phi[i];
printf("%d %d %lld\n",ca++,n,ans);
}
return 0;
}












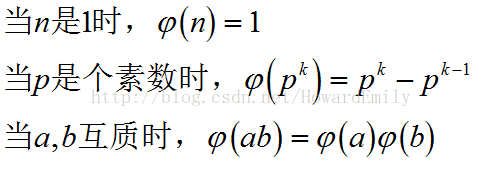

















 8139
8139











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










