Diffusion Model扩散模型原理

本文并非原创，只是个人的学习的笔记，作者只对一些步骤进行了简单的推导。具体内容请参考：

https://lilianweng.github.io/posts/2021-07-11-diffusion-models/

https://www.bilibili.com/video/BV1b541197HX?share_source=copy_web

参数重整化

若希望从高斯分布$N(\mu ,{\sigma }^2)$中采样，可以先从标准分布$N(0,1)$采样出$z$，再得到$\sigma \ast z+\mu$。这样做的好处是将随机性转移到了$z$这个常量上，而$\sigma$和$\mu$则当做放射变换网络的一部分。

前向扩散过程

从真实数据中采样一个数据点$x_0$，满足分布$x_0\sim q(x)$。让我们定义一个前向传播过程，在该过程中我们通过T步不断地向样本点中添加小量的高斯噪声，生成了一个噪声样本序列$x_1,x_2,\dots ,x_T$。步长的大小是通过一个方差集合 { β t ∈ ( 0 , 1 ) } t = 1 t \{\beta_t∈(0,1)\}^t_{t=1} {βt​∈(0,1)}t=1t​控制。
该过程是一个马尔可夫链过程

$$\begin{gathered} q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I) \\ q(x_{1:T}|x_0)=\prod _{t=1}^{T}q(x_t|x_{t-1}) \end{gathered}$$
随着步长变大，数据样本$x_0$逐渐失去其可区分的特征。最终当$T$趋于无穷时，$x_T$的值是一个各项独立的高斯分布。

我们可以使用参数重整化在任意时间步长$t$来逼近样本$x_t$，假设${\alpha }_t=1-{\beta }_t$，且${\overline{\alpha }}_t={\prod }_{i=1}^T{\alpha }_i$
$$X_t=\sqrt{{\alpha }_t}{X}_{t-1}+\sqrt{1-{\alpha }_t}{Z}_{t-1}$$
上述过程是我们从$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$使用参数重整化得到的，同理我们可以从$q(x_{t-1}|x_{t-2})=\mathcal{N}(x_{t-1};\sqrt{1-{\beta }_{t-1}}{x}_{t-2},{\beta }_{t-1}I)$中得到$X_{t-1}$的值。
$$X_{t-1}=\sqrt{{\alpha }_{t-1}}{X}_{t-2}+\sqrt{1-{\alpha }_{t-1}}{Z}_{t-2}$$
将$X_{t-1}$的值带入到$X_t$中，可得
$$\begin{gathered} X_t=\sqrt{{\alpha }_t}(\sqrt{{\alpha }_{t-1}}{X}_{t-2}+\sqrt{1-{\alpha }_{t-1}}{Z}_{t-2})+\sqrt{1-{\alpha }_t}{Z}_{t-1} \\ =\sqrt{{\alpha }_t{\alpha }_{t-1}}{X}_{t-2}+\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{Z}_{t-2}+\sqrt{1-{\alpha }_t}{Z}_{t-1} \end{gathered}$$
其中$Z_{t-1},Z_{t-2},\cdots \sim \mathcal{N}(0,I)$。而且，需要注意两个正态分布$X\sim N({\mu }_1,{\sigma }_1)$和$Y\sim N({\mu }_2,{\sigma }_2)$的叠加后的分布$aX+bY$的均值为$a{\mu }_1+b{\mu }_2$，方差为$a^2{\sigma }_1^2+b^2{\sigma }_2^2$，所以$\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{Z}_{t-2}+\sqrt{1-{\alpha }_t}{Z}_{t-1}$可以参数重整化成只含一个随机变量$Z$构成的$\sqrt{1-{\alpha }_t{\alpha }_{t-1}}Z$的形式。

则$X_t$可以写为
$$X_t=\sqrt{{\alpha }_t{\alpha }_{t-1}}{X}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\overline{Z}}_{t-1}$$
因为${\overline{\alpha }}_t={\prod }_{i=1}^T{\alpha }_i$，$X_t$最终可写为：
$$X_t=\sqrt{{\overline{\alpha }}_t}{X}_0+\sqrt{1-{\overline{\alpha }}_t}z$$
这样就得到了$q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{{\overline{\alpha }}_t}{x}_0,(1-{\overline{\alpha }}_t)I)$

通常情况下，在样本加噪时我们可以提供一个大的更新步长，即${\beta }_1<{\beta }_2<\cdots <{\beta }_T$，那么则会有${\overline{\alpha }}_1>\cdots >{\overline{\alpha }}_T$

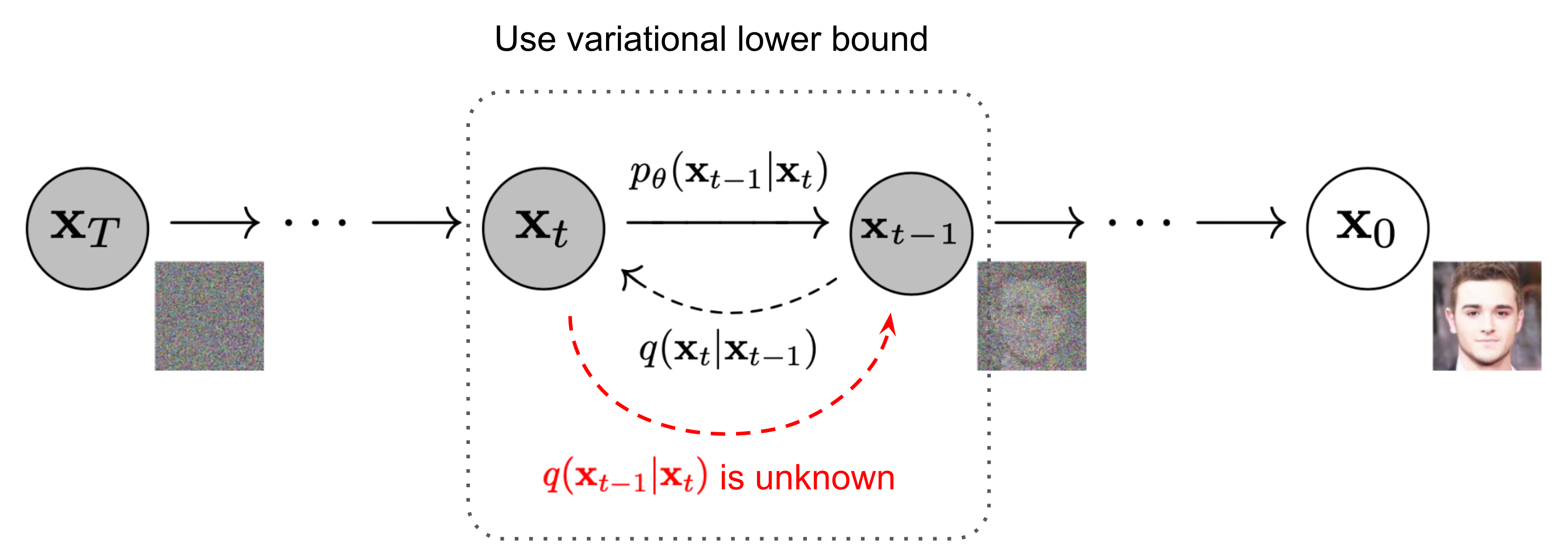
逆扩散过程

如果我们反转上述过程，尝试从$q(X_{t-1}|X_t)$中采样，我们将能够从一个高斯噪声输入$X_T\sim \mathcal{N}(0,I)$中重构出真实的样本。（逆过程是从高斯噪声中恢复原始数据）

逆扩散过程也是一个马尔科夫链过程。

需要注意的是，如果${\beta }_t$的值足够小，那么$q(X_{t-1}|X_t)$也将是一个高斯分布。但不幸的是，我们无法简单的估计$q(X_{t-1}|X_t)$，因为其估计需要使用到整个数据集。因此，我们需要学习一个模型$p_{\theta }$去逼近这些条件概率以运行这个逆扩散过程。
$$\begin{gathered} p_{\theta }(X_{0:T})=p(X_T)\prod _{t=1}^T{p}_{\theta }(X_{t-1}|X_t) \\ {p}_{\theta }(X_{t-1}|X_t)=\mathcal{N}(X_{t-1};{\mu }_{\theta }(X_t,t),\sum _{\theta }(X_t,t)) \end{gathered}$$

值得注意的是，当给定$X_0$时，这个逆条件概率是易处理的
$$q(X_{t-1}|X_t,X_0)=\mathcal{N}(X_{t-1};\tilde{\mu }(X_t,X_0),{\tilde{\beta }}_{t}I)$$
使用贝叶斯规则，我们可以得到
$$\begin{array}{rl}q(X_{t-1}|X_t,X_0)& =\frac{q(X_t,X_{t-1},X_0)}{q(X_t,X_0)}\\ & =\frac{q(X_t,X_{t-1},X_0)}{q(X_{t-1},X_0)}\ast \frac{q(X_{t-1},X_0)}{q(X_t,X_0)}\\ & =q(X_t|X_{t-1},X_0)\ast \frac{q(X_{t-1}|X_0)}{q(X_t|X_0)}\end{array}$$
由于扩散过程也是一个马尔科夫链过程，所以$q(X_t|X_{t-1},X_0)=q(X_t|X_{t-1})\sim \mathcal{N}(X_t;{\sqrt{\alpha }}_t{X}_{t-1},{\beta }_{t}I)$，后面的分式可根据前向扩展过程中的结论得到答案。
$$\begin{array}{rl}q(X_{t-1}|X_t,X_0)& =q(X_t|X_{t-1},X_0)\ast \frac{q(X_{t-1}|X_0)}{q(X_t|X_0)}\\ & \propto exp(-\frac{1}{2}(\frac{(X_t-\sqrt{{\alpha }_t}{X}_{t-1}{)}^2}{{\beta }_t}+\frac{(X_{t-1}-\sqrt{{\overline{\alpha }}_{t-1}}{X}_0{)}^2}{1-{\overline{\alpha }}_{t-1}}-\frac{(X_t-\sqrt{{\overline{\alpha }}_t}{X}_0{)}^2}{1-{\overline{\alpha }}_t})\\ & =exp(-\frac{1}{2}((\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\overline{\alpha }}_{t-1}})X_{t-1}^2-(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{X}_t+\frac{2\sqrt{{\overline{\alpha }}_t}}{1-{\overline{\alpha }}_t}{X}_0)X_{t-1}+C(X_t,X_0)))\end{array}$$
其中$(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\overline{\alpha }}_{t-1}})X_{t-1}^2-(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{X}_t+\frac{2\sqrt{{\overline{\alpha }}_t}}{1-{\overline{\alpha }}_t}{X}_0)X_{t-1}$可以看作是$a{x}^2-bx=a(x-\frac{b}{2a}{)}^2+C$。

高斯分布的概率密度函数是
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-}\frac{(x-\mu {)}^2}{2{\sigma }^2}$$
所以（分母没有2是因为已经提出去了）
$$a(x-\frac{b}{2a}{)}^2=\frac{(x-\frac{b}{2a}{)}^2}{\frac{1}{a}}=\frac{(x-\mu {)}^2}{{\sigma }^2}$$
即$q(X_{t-1}|X_t,X_0)=\mathcal{N}(X_{t-1};\tilde{\mu }(X_t,X_0),{\tilde{\beta }}_{t}I)$中的$\tilde{\mu }(X_t,X_0)$和${\tilde{\beta }}_t$可以分别写为
$$\begin{array}{rl}{\tilde{\beta }}_t& =\frac{1}{a}\\ & =\frac{1}{\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\overline{\alpha }}_{t-1}}}\\ & =\frac{1-{\overline{\alpha }}_{t-1}}{{\alpha }_t-{\alpha }_t{\overline{\alpha }}_{t-1}+1-{\alpha }_t}{\beta }_t\\ & =\frac{1-{\overline{\alpha }}_{t-1}}{1-{\overline{\alpha }}_t}{\beta }_t\end{array}$$

$$\begin{array}{rl}{\tilde{\mu }}_t(X_t,X_0)& =\frac{b}{2a}\\ & =\frac{2(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{X}_t+\frac{\sqrt{{\overline{\alpha }}_t}}{1-{\overline{\alpha }}_t}{X}_0)}{2(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\overline{\alpha }}_{t-1}})}\\ & =\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}{X}_t+\frac{\sqrt{{\overline{\alpha }}_{t-1}}{\beta }_t}{1-{\overline{\alpha }}_t}{X}_0\end{array}$$

又因为在前向扩散过程中我们得到$X_t=\sqrt{{\overline{\alpha }}_t}{X}_0+\sqrt{1-{\overline{\alpha }}_t}z$，则
$$X_0=\frac{1}{\sqrt{{\overline{\alpha }}_t}}(X_t-\sqrt{1-{\overline{\alpha }}_t}{Z}_t)$$
将$X_0$代入到$\tilde{\mu }(X_t,X_0)$中，可得
$$\begin{array}{rl}{\tilde{\mu }}_t(X_t,X_0)& =\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}{X}_t+\frac{\sqrt{{\overline{\alpha }}_{t-1}}{\beta }_t}{1-{\overline{\alpha }}_t}\frac{1}{\sqrt{{\overline{\alpha }}_t}}(X_t-\sqrt{1-{\overline{\alpha }}_t}{Z}_t)\\ & =\frac{1}{\sqrt{{\alpha }_t}}(X_t-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}{Z}_t)\end{array}$$

目标数据分布的似然函数

我们可以在负对数似然函数的基础上加上一个KL散度，于是就构成了负对数似然的上界了，上界越小，负对数似然自然也就越小，那么对数似然就越大了。
$$\begin{array}{rl}-log{p}_{\theta }(X_0)& \le -log{p}_{\theta }(X_0)+D_{KL}(q(X_{1:T}|X_0)||p_{\theta }(X_{1:T}|X_0))\\ & =-log{p}_{\theta }(X_0)+E_{X_{1:T}\sim 1(X_{1:T}|X_0)}[log\frac{q(X_{1:T}|X_0)}{p_{\theta }(X_{0:T})/p_{\theta }(X_0)}]\\ & =-log{p}_{\theta }(X_0)+E_q[log\frac{q(X_{1:T}|X_0)}{p_{\theta }(X_{0:T})}+log{p}_{\theta }(X_0)]\\ & =E_q[log\frac{q(X_{1:T}|X_0)}{p_{\theta }(X_{0:T})}]\end{array}$$

$$Let{L}_{VLB}=E_{q(X_{0:T})}[log\frac{q(X_{1:T}|X_0)}{p_{\theta }(X_{0:T})}]\ge -E_{q(X_0)}log{p}_{\theta }(X_0)$$

进一步可以写出如上公式的交叉熵的上界，接下来，我们可以对交叉熵的上界进行化简。

tips：
$$\begin{array}{r}q(X_{t-1}|X_t,X_0)=q(X_t|X_{t-1},X_0)\frac{q(X_{t-1}|X_0)}{q(X_t|X_0)}\\ =q(X_t|X_{t-1})\frac{q(X_{t-1}|X_0)}{q(X_t|X_0)}\end{array}$$

$$\begin{array}{rl}{L}_{VLB}& =E_{q(X_{0:T})}[log\frac{q(X_{1:T}|X_0)}{p_{\theta }(X_{0:T})}]\\ & =E_q[log\frac{{\prod }_{t=1}^{T}q(X_t|X_{t-1})}{p_{\theta }(X_T){\prod }_{t=1}^T{p}_{\theta }(X_{t-1}|X_t)}]\\ & =E_q[-log{p}_{\theta }(X_T)+\sum _{t=1}^{T}log\frac{q(X_t|X_{t-1})}{p_{\theta }(X_{t-1}|X_t)}]\\ & =E_q[-log{p}_{\theta }(X_T)+\sum _{t=2}^{T}log\frac{q(X_t|X_{t-1})}{p_{\theta }(X_{t-1}|X_t)}+log\frac{q(X_1|X_0)}{p_{\theta }(X_0|X_1)}]\\ & =E_q[-log{p}_{\theta }(X_T)+\sum _{t=2}^{T}log(\frac{q(X_{t-1}|X_t,X_0)}{p_{\theta }(X_{t-1}|X_t)}\ast \frac{q(X_t|X_0)}{q(X_{t-1}|X_0)})+log\frac{q(X_1|X_0)}{p_{\theta }(X_0|X_1)}]\\ & =E_q[-log{p}_{\theta }(X_T)+\sum _{t=2}^{T}log\frac{q(X_{t-1}|X_t,X_0)}{p_{\theta }(X_{t-1}|X_t)}+\sum _{t=2}^{T}log\frac{q(X_t|X_0)}{q(X_{t-1}|X_0)}+log\frac{q(X_1|X_0)}{p_{\theta }(X_0|X_1)}]\\ & =E_q[-log{p}_{\theta }(X_T)+\sum _{t=2}^{T}log\frac{q(X_{t-1}|X_t,X_0)}{p_{\theta }(X_{t-1}|X_t)}+log\frac{q(X_T|X_0)}{q(X_1|X_0)}+log\frac{q(X_1|X_0)}{p_{\theta }(X_0|X_1)}]\\ & =E_q[log\frac{q(X_T|X_0)}{p_{\theta }(X_T)}+\sum _{t=1}^T\frac{q(X_{t-1}|X_t,X_0)}{p_{\theta }(X_{t-1}|X_t)}-log{p}_{\theta }(X_0|X_1)]\\ & =E_q[D_{KL}(q(X_T|X_0)||p_{\theta }(X_T))+\sum _{t=2}^T{D}_{KL}(q(x_{t-1}|X_t,X_0)||p_{\theta }(X_{t-1}|X_t))-log{p}_{\theta }(X_0|X_1)]\end{array}$$
那么就可以得到
$$\begin{array}{rl}{L}_{VLB}& =L_T+L_{T-1}+\cdots +L_0\\ where{L}_T& =D_{KL}(q(X_T|X_0)||p_{\theta }(X_T))\\ L_t& =D_{KL}(q(X_t|X_{t+1},X_0)||p_{\theta }(X_t|X_{t+1}))for1\le t\le T-1\\ L_0& =-log{p}_{\theta }(X_0|X_1)\end{array}$$

损失函数

代码后续给出