Algorithm: Print table of 500 primes

Algorithm P

Algorithm P (Print table of 500 primes). This algorithm has two distinct
parts: Steps P1-P8 prepare an internal table of 500 primes, and steps P9-P11
print the answer in the form shown above. The latter part of the program uses
two “buffers,” in which line images are formed; while one buffer is being printed,
the other is being filled.
P1. [Start table.] Set PRIME[1] <– 2, N <– 3, J <– 1. (In this program, N runs
through the odd numbers that are candidates for primes; J keeps track of
how many primes have been found so far.)
P2. [N is prime.] Set J <– J + 1, PRIME[J] <– N.
P3. [500 found?] If J = 500, go to step P9.
P4. [Advance N.] Set N <– N + 2.
P5. [K <– 2.] Set K <– 2. (PRIME[K] will run through the possible prime divisors
of N.)
P6. [PRIME[K] \N?] Divide N by PRIME[K]; let Q be the quotient and R the
remainder. If R = 0 (hence N is not prime), go to P4.
P7. [PRIME[K] large?] If Q <= PRIME[K], go to P2. (In such a case, N must
be prime; the proof of this fact is interesting and a little unusual – see
exercise 6.)
P8. [Advance K.] Increase K by 1, and go to P6.
P9. [Print title.] Now we are ready to print the table. Advance the printer
to the next page. Set BUFFER[0] to the title line and print this line. Set
B <– 1, M <– 1.
P10. [Set up line.] Put PRIME[M], PRIME[50 + M], …, PRIME[450 + M] into
BUFFER[B] in the proper format.
P11. [Print line.] Print BUFFER[B]; set B <– 1 - B (thereby switching to the
other buffer); and increase M by 1. If M <= 50, return to P10; otherwise the
algorithm terminates. |

---

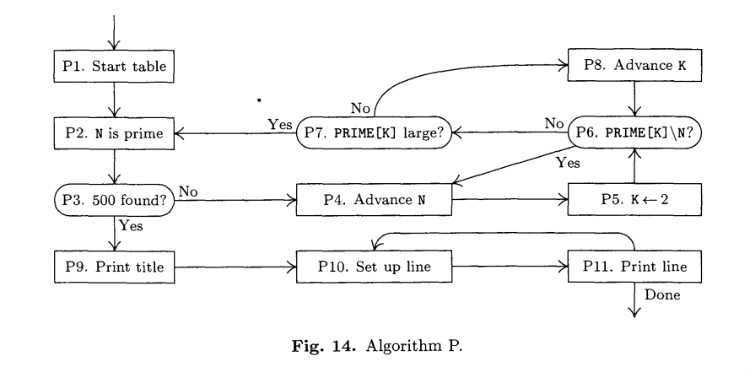
Flow diagram

---

Java program

/**
 * Created with IntelliJ IDEA.
 * User: 1O1O
 * Date: 12/17/13
 * Time: 6:52 PM
 * :)~
 * Print table of 500 primes:ALGORITHMS
 */
public class Main {

    public static void main(String[] args) {
        int[] PRIME = new int[501];
        PRIME[1] = 2;
        int N=3;
        int J=1;

        /*Kernel of the Algorithm*/
        do{
            J++;                        /*P2*/
            PRIME[J] = N;
            if(J == 500){                 /*P3*/
                break;
            }
            do{
                N+=2;                        /*P4*/
                int K=2;                     /*P5*/
                int Q, R;                     /*P6*/
                do{
                    Q = N/PRIME[K];
                    R = N%PRIME[K];
                    if(R == 0){
                        break;
                    }
                    if(Q <= PRIME[K]){         /*P7*/
                        break;
                    }
                    K++;                      /*P8*/
                }while (true);
                if(R!=0 && Q <= PRIME[K]){
                    break;
                }
            }while (true);
        }while (true);

        /*Output the 500 PRIMES*/
        System.out.println("FIRST FIVE HUNDRED PRIMES:");
        System.out.print("   ");
        for(int i=1; i<=10; i++){
            System.out.print(String.format("%5s", i));
        }
        System.out.println();
        System.out.println();
        for(int M=1; M<=50; M++){
            System.out.print(String.format("%3s", M+":"));
            for(int j=0; j<500; j+=50){
                System.out.print(String.format("%5s", PRIME[j+M]));
            }
            System.out.println();
        }
    }
}

---

Outputs

FIRST FIVE HUNDRED PRIMES:
       1    2    3    4    5    6    7    8    9   10

 1:    2  233  547  877 1229 1597 1993 2371 2749 3187
 2:    3  239  557  881 1231 1601 1997 2377 2753 3191
 3:    5  241  563  883 1237 1607 1999 2381 2767 3203
 4:    7  251  569  887 1249 1609 2003 2383 2777 3209
 5:   11  257  571  907 1259 1613 2011 2389 2789 3217
 6:   13  263  577  911 1277 1619 2017 2393 2791 3221
 7:   17  269  587  919 1279 1621 2027 2399 2797 3229
 8:   19  271  593  929 1283 1627 2029 2411 2801 3251
 9:   23  277  599  937 1289 1637 2039 2417 2803 3253
10:   29  281  601  941 1291 1657 2053 2423 2819 3257
11:   31  283  607  947 1297 1663 2063 2437 2833 3259
12:   37  293  613  953 1301 1667 2069 2441 2837 3271
13:   41  307  617  967 1303 1669 2081 2447 2843 3299
14:   43  311  619  971 1307 1693 2083 2459 2851 3301
15:   47  313  631  977 1319 1697 2087 2467 2857 3307
16:   53  317  641  983 1321 1699 2089 2473 2861 3313
17:   59  331  643  991 1327 1709 2099 2477 2879 3319
18:   61  337  647  997 1361 1721 2111 2503 2887 3323
19:   67  347  653 1009 1367 1723 2113 2521 2897 3329
20:   71  349  659 1013 1373 1733 2129 2531 2903 3331
21:   73  353  661 1019 1381 1741 2131 2539 2909 3343
22:   79  359  673 1021 1399 1747 2137 2543 2917 3347
23:   83  367  677 1031 1409 1753 2141 2549 2927 3359
24:   89  373  683 1033 1423 1759 2143 2551 2939 3361
25:   97  379  691 1039 1427 1777 2153 2557 2953 3371
26:  101  383  701 1049 1429 1783 2161 2579 2957 3373
27:  103  389  709 1051 1433 1787 2179 2591 2963 3389
28:  107  397  719 1061 1439 1789 2203 2593 2969 3391
29:  109  401  727 1063 1447 1801 2207 2609 2971 3407
30:  113  409  733 1069 1451 1811 2213 2617 2999 3413
31:  127  419  739 1087 1453 1823 2221 2621 3001 3433
32:  131  421  743 1091 1459 1831 2237 2633 3011 3449
33:  137  431  751 1093 1471 1847 2239 2647 3019 3457
34:  139  433  757 1097 1481 1861 2243 2657 3023 3461
35:  149  439  761 1103 1483 1867 2251 2659 3037 3463
36:  151  443  769 1109 1487 1871 2267 2663 3041 3467
37:  157  449  773 1117 1489 1873 2269 2671 3049 3469
38:  163  457  787 1123 1493 1877 2273 2677 3061 3491
39:  167  461  797 1129 1499 1879 2281 2683 3067 3499
40:  173  463  809 1151 1511 1889 2287 2687 3079 3511
41:  179  467  811 1153 1523 1901 2293 2689 3083 3517
42:  181  479  821 1163 1531 1907 2297 2693 3089 3527
43:  191  487  823 1171 1543 1913 2309 2699 3109 3529
44:  193  491  827 1181 1549 1931 2311 2707 3119 3533
45:  197  499  829 1187 1553 1933 2333 2711 3121 3539
46:  199  503  839 1193 1559 1949 2339 2713 3137 3541
47:  211  509  853 1201 1567 1951 2341 2719 3163 3547
48:  223  521  857 1213 1571 1973 2347 2729 3167 3557
49:  227  523  859 1217 1579 1979 2351 2731 3169 3559
50:  229  541  863 1223 1583 1987 2357 2741 3181 3571

---

Reference

<< The Art of Computer Programming: Fundamental Algorithms >> VOLUME 1, DONALD E. KNUTH