树链剖分学习&总结

于 2021-08-16 20:43:38 发布
阅读量522 收藏
点赞数
分类专栏： # ACM_模板大全 文章标签： 图论 树链剖分
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/I_have_a_world/article/details/119741169
版权

目录

前言

  1. 系统的，针对性的，学习一些铜牌算法，争取达到单挑铜牌的水平。
  2. 参考博客：oi-wiki
  3. 最后的训练时间了，那就做最重要的事情：把基础打好，我觉得针对性训练&一两年的积累，就算佛系了一些，大四也还是可以达到单挑铜首最好是银中上的水平（前提是还能一周训练3*5小时+）
    1. 习惯先想清楚再行动：做一道题，最好是尽量多的把各个细节想清楚之后再行动，除非是那种想都不用想的细节，可以直接拿起键盘就写。
    2. 要把那些铜牌银牌算法都了解一下：理解算法思想&模板总结。
      1. 比如树链剖分，抓住关键：两个dfs&一棵树的dfn序相同&线段树维护。另外，求两点间的xx，跳点不同于倍增求LCA，但是很相似

前置知识——倍增求LCA

前言

  1. 回顾，acm生涯快要结束了，cf终究没有上*1900。不过拿牌应该是ok的，最后一段时间，好好巩固基础知识打好基础！！！&（适当做一些难题拓拓上限）
  2. 放弃了学习Tarjan等更多解决LCA问题的算法，选择了刷题emmm。倍增不能解决再说吧！

性质

  1. 如果 u u u不为 v v v的祖先并且 v v v不为 u u u的祖先，那么 u , v u,v u,v分别处于LCA( u , v u,v u,v)的两棵不同子树中。
  2. 前序遍历中，LCA( S S S)出现在所有 S S S中元素之前，后序遍历中LCA( S S S)则出现在所有 S S S中元素之后。
  3. 两点集并的最近公共祖先为两点集分别的最近公共祖先的最近公共祖先，即 L C A ( A ∩ B = L C A ( L C A ( A ) , L C A ( B ) ) ) LCA(A\cap B=LCA(LCA(A),LCA(B))) LCA(A∩B=LCA(LCA(A),LCA(B)))。
  4. 两点的最近公共祖先必定处在树上两点间的最短路上。
  5. d ( u , v ) = h ( u ) + h ( v ) − 2 h ( L C A ( u , v ) ) d(u,v)=h(u)+h(v)-2h(LCA(u,v)) d(u,v)=h(u)+h(v)−2h(LCA(u,v))，其中 d d d是树上两点间的距离， h h h代表某点到树根的距离。

求法1：朴素算法（单词查询随机复杂度为 O ( log ⁡ n ) O(\log n) O(logn)，但是可以很容易卡到 O ( n ) O(n) O(n)）

  1. 每次深度较大的向上跳（一步一步向上跳），知道两个点相遇。

求法2：倍增算法（最经典的LCA求法&朴素算法的倍增改进算法&预处理复杂度 O ( n log ⁡ n ) O(n\log n) O(nlogn)，单次查询复杂度 O ( log ⁡ n ) O(\log n) O(logn)）

  1. 设最开始 u , v u,v u,v两点深度相差为 y y y，先对 y y y进行二进制拆分，使两点深度一致。
  2. 然后从高位到地位不断尝试，如果f[u][i]!=f[v][i]就跳，否则不跳。循环结束即得到LCA(u,v)的两个儿子，最后处理以下即可（fa[u][0]）。
  3. **小知识：**另外倍增算法可以通过交换fa数组的两维使较小维放在前面。这样可以减小chche miss次数，提高程序效率。

模板（知道原理很简单，以下一遍过）

// 其中fa[i][0]在dfs时求出
void init_LCA() {
    for (int j = 1; j <= 20; j++) {
        for (int i = 1; i <= n; i++) {
            fa[i][j] = fa[fa[i][j - 1]][j - 1];
        }
    }
}
//返回的是LCA节点
int LCA(int x, int y) {
    if (dep[x] < dep[y]) swap(x, y);
    int diff = dep[x] - dep[y];
    for (int j = 20; j >= 0; j--)
        if (diff >= (1 << j))
            x = fa[x][j], diff -= (1 << j);  //差点忘了diff-=(1<<j)
    if (x == y) return x;//这里也要注意，不然就是fa[LCA(x,y)][0]了
    for (int j = 20; j >= 0; j--)
        if (fa[x][j] != fa[y][j]) x = fa[x][j], y = fa[y][j];
    return fa[x][0];
}

题目1：查询树上两点的距离（性质5： d i s t [ u , v ] = d i s t [ u ] + d i s t [ v ] − 2 ∗ d i s t [ L C A ( u , v ) ] dist[u,v]=dist[u]+dist[v]-2*dist[LCA(u,v)] dist[u,v]=dist[u]+dist[v]−2∗dist[LCA(u,v)]）

  1. 传送门：How far away ？ HDU - 2586
  2. 题意：不超过10组样例，一个村庄 n 户人，有 n-1 条无向边连接 n 户人，每组样例不超过100次询问，询问两户人家的距离。
    1. 1 ≤ n ≤ 40000 ， 0 ≤ 边 ≤ 40000 1\le n\le 40000，0\le 边\le 40000 1≤n≤40000，0≤边≤40000
  3. 题解：略
  4. 代码：
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
#define int long long
#define pii pair<int, int>
#define x first
#define y second
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
template <class T>
void read(T &x) {
    T res = 0, f = 1;
    char c = getchar();
    while (!isdigit(c)) {
        if (c == '-') f = -1;
        c = getchar();
    }
    while (isdigit(c)) res = (res << 3) + (res << 1) + (c - '0'), c = getchar();
    x = res * f;
}
const int N = 4e4 + 100;
int n, q, u, v, w;
vector<pii> g[N];
int dep[N], fa[N][23], dis[N];
void init() {
    for (int i = 1; i <= n; i++) g[i].clear();
    memset(fa, 0, sizeof(fa));
    memset(dep, 0, sizeof(dep));
    memset(dis, 0, sizeof(dis));
}
void dfs(int x, int Fa) {
    for (auto i : g[x]) {
        if (i.x == Fa) continue;
        dis[i.x] = dis[x] + i.y;
        dep[i.x] = dep[x] + 1;
        fa[i.x][0] = x;
        dfs(i.x, x);
    }
}
void init_LCA() {
    for (int j = 1; j <= 20; j++) {
        for (int i = 1; i <= n; i++) {
            fa[i][j] = fa[fa[i][j - 1]][j - 1];
        }
    }
}
int LCA(int x, int y) {
    if (dep[x] < dep[y]) swap(x, y);
    int diff = dep[x] - dep[y];
    for (int j = 20; j >= 0; j--)
        if (diff >= (1 << j))
            x = fa[x][j], diff -= (1 << j);  //差点忘了-=(1<<j)
    if (x == y) return x;
    for (int j = 20; j >= 0; j--)
        if (fa[x][j] != fa[y][j]) x = fa[x][j], y = fa[y][j];
    return fa[x][0];
}
signed main() {
    int T;
    read(T);
    while (T--) {
        read(n), read(q);
        init();
        for (int i = 1; i < n; i++) {
            read(u), read(v), read(w);
            g[u].push_back({v, w}), g[v].push_back({u, w});
        }
        dis[1] = 0, dep[1] = 0;
        dfs(1, -1);
        //为什么初始化为0，就ok？请看LCA部分，只要不影响LCA部分就没问题。
        init_LCA();
        int ans = 0;
        while (q--) {
            read(u), read(v);
            ans = dis[u] + dis[v] - 2 * dis[LCA(u, v)];
            // cout<<">>>>>>>>>>";
            printf("%lld\n", ans);
        }
    }
    return 0;
}
/*
样本输入
2
3 2
1 2 10
3 1 15
1 2
2 3

2 2
1 2 100
1 2
2 1
样本输出
10
25
100
100
*/

树链剖分的思想及能解决的问题

  1. 把整棵树剖分成若干条链，使它组合成线性结构，然后用其他的数据结构维护信息。
  2. 树链剖分有多种形式，如重链剖分，长链剖分等，大多数形况下，“树链剖分”都指“重链剖分”。
  3. 重链剖分可以将树上的任意一条路径划分成不超过O(logn)条连续的链。
  4. 另外，重链剖分还可以保证划分出的每条链上的节点DFS序连续，甚至每棵子树上的节点DFS序连续，因此可以方便的用一些维护序列的数据结构（比如线段树）来维护树上路径的信息。如：
    1. 修改树上两点之间的路径上所有点的值。
    2. 查询树上两点之间的路径上节点权值的和/极值/其它（在序列上可以用数据结构维护，便于合并的信息）。
  5. 除了配合数据结构来维护树上路径信息，树剖还可以用来O(logn)（且常数较小）地来求LCA。在某些题目中，还可以利用它其性质来灵活的运用树剖。
    1. 因为上面这句话重链剖分可以将树上的任意一条路径划分成不超过O(logn)条连续的链。
  6. 总结能解决的问题：
    1. O(logn)求LCA
    2. 维护树上路径的信息，比如修改某个点，查询和/极值、以及其他能用线段树维护的信息（比如删点&维护子树大小）。

重链剖分的操作

知道重链剖分的操作，其他xx链剖分的操作也就很容易写出来了

一些定义

  1. 重子节点：其子节点中子树最大的子节点。如果有多个子树最大的子节点，取其一。如果没有子节点，就无重子节点。
  2. 轻子节点：剩余的所有子节点。
  3. 重边/轻边：从一个节点到其重子节点的边为重边，否则叫轻边。
  4. 重链：若干条首尾衔接的重边构成重链。把落单的节点也当作重链，那么整棵树就被剖分成若干条重链。
    在这里插入图片描述

代码实现

  1. 树剖的实现分两个DFS的过程（其他就是线段树等维护信息的东西了）。
    1. 第一个DFS记录每个节点的父节点（father）、深度（deep）、子树大小（size）、重子节点（hson）。
    2. 第二个DFS记录所在链的链顶（top，应初始化为节点本身）、重边优先遍历时的DFS序（dfn）、DFS序对应的节点编号（rank）。
  2. 给出一些定义：
    在这里插入图片描述
  3. 我们进行两遍DFS预处理出这些值，其中第一次DFS求出 f a ( x ) , d e p ( x ) , s i z ( x ) , s o n ( x ) fa(x),dep(x),siz(x),son(x) fa(x),dep(x),siz(x),son(x)，第二次DFS求出 t o p ( x ) , d f n ( x ) , r n k ( x ) top(x),dfn(x),rnk(x) top(x),dfn(x),rnk(x)。
//这里根节点的父亲fa是0，深度dep为1
void dfs1(int x, int fu) {
    //处理叶子节点可以放在这里
    son[x] = -1;  //没有重儿子
    siz[x] = 1;   //大小为1
    for (auto i : g[x]) {
        if (i == fu) continue;
        dep[i] = dep[x] + 1;  //深度
        fa[i] = x;            //父亲
        dfs1(i, x);
        siz[x] += siz[i];
        if (son[x] == -1 || siz[i] > siz[son[x]]) son[x] = i;  //更新重儿子
    }
}
void dfs2(int x, int t) {
    //遍历到这个点的时候处理这个点
    top[x] = t;                // t为重链顶端，x属于重链t
    dfn[x] = ++cnt;            //重链优先的dfs序
    rnk[cnt] = x;              // dfs序为cnt的节点为x
    if (son[x] == -1) return;  //没有重儿子
    dfs2(son[x], t);
    for (auto i : g[x]) {
        if (i == fa[x]) continue;
        if (i == son[x]) continue;  //重儿子已经提前遍历过了
        dfs2(i, i);                 //自己是自己的重链顶端
    }
}

重链剖分的性质

  1. 树上每个节点都属于且仅属于一条重链。
  2. 所有的重链将整棵树完全剖分。
  3. 在剖分时重边优先遍历，最后树的DFN序上，重链内的DFN序是连续的。按DFN排序后的序列即为剖分后的链。
  4. 一棵子树内的DFN序是连续的。
  5. 可以发现，当我们向下经过一条轻边时，所在子树的大小至少会除以2。因此，对于树上的任意一条路径，把它拆分成从lca分别向两边往下走，分别最多走O(logn)次，因此，树上的每条路径都可以被拆分成不超过O(logn)条重链。

常见应用

应用1：路径上维护

  1. 比如用树链剖分求树上两点路径权值和。
    1. 链上的DFS序是连续的，可以使用线段树，树状数组维护。
    2. 每次选择深度交大的链往上跳，知道两点在同一条链上。
    3. 同样的跳链结构适用于维护、统计路径上的其他信息。
  2. 另外线段树能维护的东西都能求。
  3. 求LCA的操作算是路径上维护的最基本的操作。

应用2：子树维护

  1. 比如将以 x 为根的子树的所有节点的权值增加 v 。
    1. 在DFS搜索的时候，子树中的节点的DFS序是连续的。
    2. 每一个节点记录bottom表示所在子树连续区间末端的结点（ps：其实好像不用特意记录，查询子树大小即可，因为连续）。
    3. 这样就把子树信息转化为连续的一段区间信息。

应用3：求最近公共祖先

  1. 不断往上跳重链，当跳到同一条重链上时，深度较小的结点即为LCA。
  2. 向上跳重链时需要先跳所在重链顶端深度较大的那个。
int lca(int u, int v) {
    while (top[u] != top[v]) {
        if (dep[top[u]] > dep[top[v]])
            u = fa[top[u]];
        else
            v = fa[top[v]];
    }
    return (dep[u] > dep[v]) ? v : u;
}

了解：怎么有理有据卡树剖

在这里插入图片描述

模板例题

题目1：树的统计 LibreOJ - 10138 （单结点修改权值&查询路径最大权值&查询路径权值和）

树的统计 LibreOJ - 10138

  1. 题意：
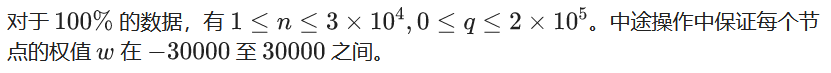
    在这里插入图片描述
  2. 数据范围：
    在这里插入图片描述
  3. 题解：树链剖分之后线段树维护即可，查询路径的时候需要用到和LCA差不多的操作。每次查询时间复杂度 O ( l o g 2 n ) O(log^2n) O(log2n)（实际上重链个数很难达到O(logn)（可以用完全二叉树卡满），所以树剖在一半情况下常熟较小）。
  4. 代码：
#include <bits/stdc++.h>
// #define int long long
#define lc p << 1
#define rc p << 1 | 1
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int N = 3e4 + 5;
const int inf = 2e9;
int n, w[N];
vector<int> g[N];
int siz[N], top[N], son[N], dep[N], fa[N], dfn[N], rnk[N], cnt;
struct SegTree {
    int sum[N << 2], mx[N << 2];
    void build(int p, int l, int r) {
        if (l == r) {
            sum[p] = mx[p] = w[rnk[l]];
            return;
        }
        int mid = (l + r) >> 1;
        build(lc, l, mid);
        build(rc, mid + 1, r);
        sum[p] = sum[lc] + sum[rc];
        mx[p] = max(mx[lc], mx[rc]);
    }
    //查询区间最大值
    int query1(int p, int l, int r, int x, int y) {
        if (l > y || r < x)
            return -inf;  //然后下面就不用判断x or y与mid的关系，直接return即可
        if (x <= l && r <= y) return mx[p];
        int mid = (l + r) >> 1;
        return max(query1(lc, l, mid, x, y), query1(rc, mid + 1, r, x, y));
    }
    //查询区间和
    int query2(int p, int l, int r, int x, int y) {
        if (l > y || r < x) return 0;
        if (x <= l && r <= y) return sum[p];
        int mid = (l + r) >> 1;
        return query2(lc, l, mid, x, y) + query2(rc, mid + 1, r, x, y);
    }
    //这里是单点修改
    //整颗树修改的话改成区间修改就ok了。裸的线段树还是熟悉的
    void update(int p, int l, int r, int x, int k) {
        if (l == r) {
            sum[p] = mx[p] = k;
            return;
        }
        int mid = (l + r) >> 1;
        if (x <= mid)
            update(lc, l, mid, x, k);
        else
            update(rc, mid + 1, r, x, k);
        sum[p] = sum[lc] + sum[rc];
        mx[p] = max(mx[lc], mx[rc]);
    }
} st;
// querymax和querysum的操作基本上完全一样
//往上跳点，和倍增求LCA不一样。
//倍增求LCA是怎样跳点来着？每次跳到相同深度，然后同时往上慢慢跳
//树链剖分的性质很重要！！！
int querymax(int x, int y) {
    int res = -inf, fx = top[x], fy = top[y];
    while (fx != fy) {
        //也是首先跳深度大的，没跳一次判断一下是否在一棵树
        if (dep[fx] >= dep[fy])
            res = max(res, st.query1(1, 1, n, dfn[fx], dfn[x])), x = fa[fx];
        else
            res = max(res, st.query1(1, 1, n, dfn[fy], dfn[y])), y = fa[fy];
        fx = top[x];
        fy = top[y];
    }
    if (dfn[x] < dfn[y])
        res = max(res, st.query1(1, 1, n, dfn[x], dfn[y]));
    else
        res = max(res, st.query1(1, 1, n, dfn[y], dfn[x]));
    return res;
}
int querysum(int x, int y) {
    int res = 0, fx = top[x], fy = top[y];
    //跳到fx==fy即在同一树链上为止
    while (fx != fy) {
        if (dep[fx] >= dep[fy])
            res += st.query2(1, 1, n, dfn[fx], dfn[x]), x = fa[fx];
        else
            res += st.query2(1, 1, n, dfn[fy], dfn[y]), y = fa[fy];
        //这里y=fa[fy]也是关键，跳到了另一条重链上了
        fx = top[x];
        fy = top[y];
    }
    //同一条重链上，dfs序小的深度小
    if (dfn[x] < dfn[y])
        res += st.query2(1, 1, n, dfn[x], dfn[y]);
    else
        res += st.query2(1, 1, n, dfn[y], dfn[x]);
    return res;
}
//这里根节点的父亲是0，深度是1
void dfs1(int x, int fu) {
    //处理叶子节点可以放在这里
    son[x] = -1;  //没有重儿子
    siz[x] = 1;   //大小为1
    for (auto i : g[x]) {
        if (i == fu) continue;
        dep[i] = dep[x] + 1;  //深度
        fa[i] = x;            //父亲
        dfs1(i, x);
        siz[x] += siz[i];
        if (son[x] == -1 || siz[i] > siz[son[x]]) son[x] = i;  //更新重儿子
    }
}
void dfs2(int x, int t) {
    //遍历到这个点的时候处理这个点
    top[x] = t;      // t为重链顶端，x属于重链t
    dfn[x] = ++cnt;  //重链优先的dfs序
    rnk[cnt] = x;    // dfs序为cnt的节点为x
    if (son[x] == -1) return;  //没有重儿子
    dfs2(son[x], t);
    for (auto i : g[x]) {
        if (i == fa[x]) continue;
        if (i == son[x]) continue;  //重儿子已经提前遍历过了
        dfs2(i, i);  //自己是自己的重链顶端
    }
}
signed main() {
    cin >> n;
    for (int i = 1, a, b; i < n; i++) {
        cin >> a >> b;
        g[a].push_back(b), g[b].push_back(a);
    }
    for (int i = 1; i <= n; i++) cin >> w[i];
    dep[1] = 1;  // 1的深度为1
    dfs1(1, 0);
    dfs2(1, 1);
    st.build(1, 1, n);
    int q, u, v;
    char op[10];
    cin >> q;
    while (q--) {
        scanf("%s%d%d", op, &u, &v);
        if (op[1] == 'H') st.update(1, 1, n, dfn[u], v);  // change
        // else
        // cout << ">>>>>>>>>>>>>>>>>>>>>>>>";
        if (op[1] == 'M') printf("%d\n", querymax(u, v));
        if (op[1] == 'S') printf("%d\n", querysum(u, v));
    }
    return 0;
}

专题训练

  1. 专题地址：树链剖分练习题
  2. 总结经验：
    1. 之前时间多，刷专题的时候都是先刷简单的，然后再刷难的。现在一个专题都不一定刷得完，那就首先刷能让自己收获更大的题目吧。

题目1：P4374 [USACO18OPEN]Disruption P（边权转化为点权&树链剖分）

P4374 [USACO18OPEN]Disruption P

  1. 题意：有 n n n 个农场，n-1 条双向道路（构成一棵树），长度都为1。另外有 q 条双向道路{u,v,k}分别表示 u，v结点之间有一条长度为k的双向道路。
    1. 要求输出，第 i 条线段断了之后，最短的可替代道路的长度（某条线断了之后，树分成两半，求能将它们连起来的最短道路的长度），如果不存在则输出 -1。
    2. 1 ≤ n , q ≤ 5 e 4 1\le n,q\le 5e4 1≤n,q≤5e4，另外所以道路长度都是一个至多为 1e9 的正整数。
  2. 题解：
    1. 替代道路：原树中u，v路径间的线段都可以被{u,v,k}替代——树链剖分的路径操作
    2. 边转化为点：建图的时候注意一下就ok
    3. 具体的见代码，不难。
  3. 代码：
#include <bits/stdc++.h>
// #define int long long
#define lc p << 1
#define rc p << 1 | 1
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int N = 1e5 + 5;  // 5e4*2
const int inf = 2e9;
int n, q, u, v;
vector<int> g[N];
int dep[N], son[N], siz[N], fa[N];  // dfs1要维护的
int dfn[N], rnk[N], top[N], cnt;    // dfs2要维护的
void dfs1(int x, int fu) {
    son[x] = -1;
    siz[x] = 1;
    for (auto i : g[x]) {
        if (i == fu) continue;
        dep[i] = dep[x] + 1;
        fa[i] = x;
        dfs1(i, x);
        siz[x] += siz[i];
        if (son[x] == -1 || siz[i] > siz[son[x]]) son[x] = i;
    }
}
// t表示top
void dfs2(int x, int t) {
    top[x] = t;
    dfn[x] = ++cnt;
    rnk[cnt] = x;
    if (son[x] == -1) return;  //叶子结点没有重儿子
    dfs2(son[x], t);
    for (auto i : g[x]) {
        if (i == fa[x]) continue;
        if (i == son[x]) continue;
        dfs2(i, i);
    }
}
//这一题，需要线段树维护最小值
struct SegTree {
    int mi[N << 2], tag[N << 2];
    void build(int p, int l, int r) {
        mi[p] = tag[p] = inf;
        if (l == r) return;
        int mid = (l + r) >> 1;
        build(lc, l, mid);
        build(rc, mid + 1, r);
    }
    void pushdown(int p) {
        mi[lc] = min(mi[lc], tag[p]);
        tag[lc] = min(tag[lc], tag[p]);
        mi[rc] = min(mi[rc], tag[p]);
        tag[rc] = min(tag[rc], tag[p]);
        tag[p] = inf;
    }
    //区间维护最小值
    //这一题，可以从大到小排序之后再update，就不用min
    void update(int p, int l, int r, int x, int y, int k) {
        if (x <= l && r <= y) {
            mi[p] = min(mi[p], k);
            tag[p] = min(tag[p], k);
            return;
        }
        pushdown(p);
        int mid = (l + r) >> 1;
        if (x <= mid) update(lc, l, mid, x, y, k);
        if (y > mid) update(rc, mid + 1, r, x, y, k);
        mi[p] = min(mi[lc], mi[rc]);
    }
    //单点查询最小值
    int query(int p, int l, int r, int x) {
        if (x < l || x > r) return inf;
        if (l == r) return mi[p];
        pushdown(p);
        int mid = (l + r) >> 1;
        return min(query(lc, l, mid, x), query(rc, mid + 1, r, x));
    }
} st;
void update(int x, int y, int k) {
    int fx = top[x], fy = top[y];
    while (fx != fy) {
        if (dep[fx] >= dep[fy])
            st.update(1, 1, 2 * n - 1, dfn[fx], dfn[x], k), x = fa[fx];
        else
            st.update(1, 1, 2 * n - 1, dfn[fy], dfn[y], k), y = fa[fy];
        fx = top[x];
        fy = top[y];
    }
    if (dep[x] <= dep[y])
        st.update(1, 1, 2 * n - 1, dfn[x], dfn[y], k);
    else
        st.update(1, 1, 2 * n - 1, dfn[y], dfn[x], k);
}
signed main() {
    cin >> n >> q;
    for (int i = 1; i < n; i++) {
        cin >> u >> v;
        g[u].push_back(n + i), g[n + i].push_back(u);
        g[v].push_back(n + i), g[n + i].push_back(v);
    }
    dep[1] = 1;
    dfs1(1, 0);
    dfs2(1, 1);
    st.build(1, 1, 2 * n - 1);
    // for (int i = 1; i <= n; i++) {
    // cout << ">>>" << i << " " << dfn[i] << endl;
    // }
    int k;
    while (q--) {
        scanf("%d%d%d", &u, &v, &k);
        update(u, v, k);
    }
    for (int i = 1, ans; i < n; i++) {
        ans = st.query(1, 1, 2 * n - 1, dfn[n + i]);
        if (ans == inf) ans = -1;
        printf("%d\n", ans);
    }
    return 0;
}

题目2：P2486 [SDOI2011]染色（维护路径颜色段和–相邻相同的颜色算一段）

  1. P2486 [SDOI2011]染色
  2. 题意：
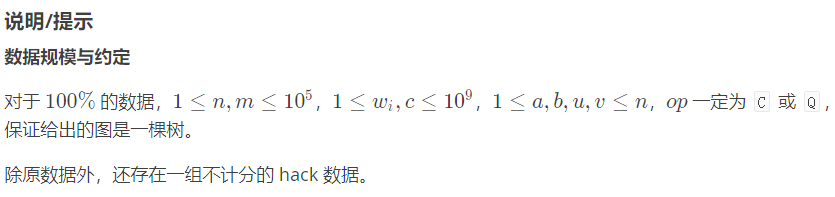
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
  3. 题解提示：
    1. 只需要在普通的维护区间和的线段树中维护区间端点的颜色即可
    2. 但是操作还是有点麻烦，还是不熟悉线段树emm（对线段树理解不够深入）
  4. 收获总结：对线段树有了更深的理解
    1. 树链剖分容易将结点序和dfs序搞混淆，要注意
    2. 在线段树查询的时候，到最后一层一定有l==xorr=y。
      在这里插入图片描述
  5. 代码：
// https://www.luogu.com.cn/problem/P2486
#include <bits/stdc++.h>
#define lc p << 1
#define rc p << 1 | 1
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int N = 1e5 + 5;
int n, m, w[N];
vector<int> g[N];
int dep[N], siz[N], fa[N], son[N];
int cnt, top[N], dfn[N], rnk[N];
void dfs1(int x, int fu) {
    son[x] = -1;
    siz[x] = 1;
    for (auto i : g[x]) {
        if (i == fu) continue;
        dep[i] = dep[x] + 1;
        fa[i] = x;
        dfs1(i, x);
        siz[x] += siz[i];
        if (son[x] == -1 || siz[i] > siz[son[x]]) son[x] = i;
    }
}
void dfs2(int x, int t) {
    top[x] = t;
    dfn[x] = ++cnt;
    rnk[cnt] = x;
    if (son[x] == -1) return;
    dfs2(son[x], t);
    for (auto i : g[x]) {
        if (i == fa[x]) continue;
        if (i == son[x]) continue;
        dfs2(i, i);
    }
}
int Lc, Rc;
//看起来复杂，实际上就比普通维护区间和线段树多维护了区间左右颜色
struct SegTree {
    // sum[p]表示区间p的颜色段数
    // if tag[p]>0:表示区间p都修改成颜色tag[p]
    int sum[N << 2], tag[N << 2], L[N << 2],
        R[N << 2];  // L[p]，R[p]表示区间p的左右端颜色
    void pushup(int p) {
        L[p] = L[lc], R[p] = R[rc];
        sum[p] = sum[lc] + sum[rc];
        if (R[lc] == L[rc]) sum[p]--;
    }
    void build(int p, int l, int r) {
        if (l == r) {
            L[p] = R[p] = w[rnk[l]];
            sum[p] = 1;
            return;
        }
        int mid = (l + r) >> 1;
        build(lc, l, mid);
        build(rc, mid + 1, r);
        pushup(p);
    }
    void pushdown(int p) {
        if (tag[p]) {
            sum[lc] = sum[rc] = 1;
            L[lc] = R[lc] = L[rc] = R[rc] = tag[p];
            tag[lc] = tag[rc] = tag[p];
            tag[p] = 0;
        }
    }
    //维护区间左右颜色，即可维护区间和
    void update(int p, int l, int r, int x, int y, int k) {
        if (x <= l && r <= y) {
            sum[p] = 1;
            tag[p] = k;
            L[p] = R[p] = k;  //这款线段树，只需要多维护L[p]和R[p]
            return;
        }
        pushdown(p);
        int mid = (l + r) >> 1;
        if (mid >= x) update(lc, l, mid, x, y, k);
        if (mid < y) update(rc, mid + 1, r, x, y, k);
        pushup(p);
    }
    //?这里应该还要修改一下
    int query(int p, int l, int r, int x, int y) {
        if (x <= l && r <= y) {
            if (l == x) Lc = L[p];
            if (r == y) Rc = R[p];
            //一般都是l<x&&y<r，只有可能在边界l==x||r==y
            return sum[p];
        }
        pushdown(p);
        int res = 0;
        int mid = (l + r) >> 1;
        if (mid >= x) res += query(lc, l, mid, x, y);
        if (mid < y) res += query(rc, mid + 1, r, x, y);
        if (mid >= x && mid < y) res -= (R[lc] == L[rc]);
        return res;
    }
} st;
void add(int x, int y, int k) {
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y);
        st.update(1, 1, n, dfn[top[x]], dfn[x], k);
        x = fa[top[x]];  //交换之后只对 x 操作，nice！
    }
    if (dep[x] > dep[y]) swap(x, y);
    st.update(1, 1, n, dfn[x], dfn[y], k);
}
int ask(int x, int y) {
    int res = 0, pre1 = -1, pre2 = -1;
    // dbg(1);
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x, y), swap(pre1, pre2);
        res += st.query(1, 1, n, dfn[top[x]], dfn[x]);
        if (Rc == pre1) res--;  // Rc即为dfn[x]的颜色
        pre1 = Lc;              //只操作 x 是有很多好处的
        x = fa[top[x]];
    }
    if (dep[x] > dep[y]) swap(x, y), swap(pre1, pre2);
    res += st.query(1, 1, n, dfn[x], dfn[y]);
    if (Lc == pre1) res--;
    if (Rc == pre2) res--;
    return res;
}
signed main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> w[i];
    for (int i = 1; i < n; i++) {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dep[1] = 1;
    dfs1(1, 0);
    dfs2(1, 1);
    st.build(1, 1, n);
    char ch;
    int a, b, c;
    while (m--) {
        cin >> ch;
        if (ch == 'C') {
            scanf("%d%d%d", &a, &b, &c);
            add(a, b, c);
        } else {
            scanf("%d%d", &a, &b);
            printf("%d\n", ask(a, b));
        }
    }
    return 0;
}
I_have_a_world
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
树链剖分详解
算法小猪的博客
08-13 1291
目录一、树链剖分相关概念1.为啥要剖分2.轻边和重边3.轻重边路径剖分的性质二、树链剖分的实现1.重链剖分 一、树链剖分相关概念 1.为啥要剖分 1.可以维护树路径上的信息(维护) 2.将一棵树划分成若干条链，用数据结构去维护每条链，复杂度为O(logN)O(logN)O(logN)。(复杂度低) 2.轻边和重边 将树中的边分为：轻边和重(zhong)边 定义size(x)size(x)size(x)为以xxx为根的子树的节点个数。 令vvv为xxx的儿子节点中sizesizesize值最大的节点，那么边(
算法学习笔记：树链剖分
Plozia 的小窝
03-09 352
算法学习笔记：树链剖分1. 前言2. 详解 1. 前言 树链剖分，是一种树上的算法，将树划分为若干条链，然后利用线段树来处理树上信息。 在学树链剖分之前，你需要了解的知识： DFS 序。 线段树的基础操作。 2. 详解 模板题：P3384 【模板】轻重链剖分 ...
树链剖分详解【后期会不断更新】
IDDFS
07-30 1239
知识准备 1.DFS； 2.线段树。 相信DFS大家都会，估计只有线段树了。 如果有不会的请点这里：线段树系列文章（未完） 何谓树链剖分？ 就是将一棵树分成许多条链，使得树中所有节点都被包含在这些链里。 （换句话说：就是一种使你的代码瞬间增加1KB的算法。） 怎么剖分？ 1.随便剖分 随便找一个节点，将它作为链头向下剖分。 2.随机剖分 随便剖分+一点特判。 3.轻重...
LCA+RMQ+树状数组poj2763
龙崎的专栏
08-10 578
Language: Default Housewife Wind Time Limit: 4000MS   Memory Limit: 65536K Total Submissions: 5754   Accepted: 1442 Description After their royal wedding, Jiajia an
poj 2763(树链剖分)
俯瞰风景
10-15 925
题意：有一个人在一棵树的某个节点s，然后给出了树的每条边都有一个权值，有两种操作，0 a 是问从节点s到a的路径权值和，然后a就成了s，1 a b把第a条边权值变为b。 题解：边权转点权的模板题。#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N = 100005; s
NOIP 树链剖分 NOIP 树链剖分
10-30
NOIP 树链剖分 NOIP 树链剖分
树链剖分算法.pptx
09-03
树链剖分，计算机术语，指一种对树进行划分的算法，它先通过轻重边剖分将树分为多条链，保证每个点属于且只属于一条链，然后再通过数据结构（树状数组、BST、SPLAY、线段树等）来维护每一条链
树链剖分学习笔记（自用）
最新发布
12-25
树链剖分学习笔记（自用）
第5章 树链剖分 测试数据.rar
12-02
树链剖分是一种高效处理树型结构的算法，尤其在解决与树的边查询和修改有关的问题时，它能提供显著的效率提升。这一技术在信息学奥赛中经常被用到，帮助参赛者快速解决复杂的树形问题。在本章的测试数据中，你将有...
树链剖分模板题
05-19
#include #include #include #define N 30003 #define INF 2147483647 using namespace std; int n,f[N][20],dep[N],siz[N],son[N],top[N],tot,pos[N],w[N]; int Max[N*4],Sum[N*4];...vector <int> to[N];...
HDU 3966 树链剖分
Dan__ge的博客
07-10 1463
点击打开链接 题意：给一个树，三个操作，一个询问点的权值，一个将u到v路径上的点的权值增加，一个是减少 思路：还是比较裸的模版题，线段树改为区间更新就好了#pragma comment(linker, "/STACK:1024000000,1024000000") #include #include #include #include #include #include using
图论学习:树上问题（LCA，树链剖分）
qq_43597227的博客
03-24 608
图论:树上问题（LCA，树链剖分） LCA（Least Common Ancestors）：最近公共祖先 对于有根树T的两个结点u、v，最近公共祖先LCA(T,u,v)表示一个结点x，满足x是u和v的祖先且x的深度尽可能大。在这里，一个节点也可以是它自己的祖先 ——百度百科 求LCA的常用算法： 1.离线算法：LCA（tarjan） 2.在线算法：倍增LCA和ST表 1. LCA（Tarjan）：...
树链剖分及应用
weixin_43184669的博客
02-06 415
定义：   将整棵树剖分为若干条链，使它组合成线性结构，然后用其他的数据结构维护信息。就是一种技巧，为了方便处理问题。   形式：重链剖分，长链剖分等。此处讲述重链剖分。 重链剖分：   可以将树上的任意一条路径划分成不超过 lognlognlogn 条连续的链，每条链上的点深度互不相同（即是自底向上的一条链，链上所有点的 LCALCALCA 为链的一个端点）。还能保证划分出的每条链上的节点 DF...
poj 3237 Tree（树链剖分---边权化点权）
雪的期许
08-13 509
Tree Time Limit: 5000MS   Memory Limit: 131072K Total Submissions: 11989   Accepted: 3088 Description You are given a tree with N nodes. The tree’s nodes ...
【例题】【树链剖分】
ANG
12-25 715
1、 【USACO 2011 Dec Gold 】种草 时间限制 : 10000 MS 空间限制 : 65536 KB问题描述 农夫约翰有N块贫瘠的牧场(2 <= N <= 100,000)，有N-1条双向道路将这N个牧场连接了起来，每两个牧场间都有且仅有一条路径可相互到达。著名奶牛贝西经常抱怨：为什么连接牧场的道路上没有草可吃呢? 约翰非常喜欢贝西，今天约翰终于决定要在道路上种草了。约
树链剖分详解及模板
热门推荐
大神养成中.....
10-21 2万+
这几天学习了一下树链剖分，顺便写一下我的理解、 早上看了一下别人的讲解，云里雾里，终于算是搞懂了、 树链剖分是解决在树上进行插点问线，插线问点等一系列树上的问题 假如现在给你一棵树，然后没两条边之间有一条权值，有一些操作，1：x---y之间的最大权值是多少，2：改变x---y之间的权值 当前这样的操作有很多，如果直接用暴力的方法的话肯定不行，那么就要想一个好的方法，我们可以想一
树的操作（换根树剖）
苟为蒟蒻又何妨
06-30 1101
描述 XXX和 YYY在愉快地刷题。有一道题是这样的：给你一棵 n 个节点的有根树，每个节点有 一个权植。你要支持两种操作：查询以某棵树为根的子树的权值和，给以某个节点为根的整 棵子树的所有点的权值都加上一个值。机智的 XXX 很开心地用LLL教授 讲过的某些东西水水水水过了这道题。 但是可怕的出题人又增加了一种操作：将根节点改为第 u 号节点。于是XXX和YYY 就不会 做了。按照一惯的逻辑...
初学树剖的一些理解
Serene
04-26 1259
省选前刚学了树剖的模板，感觉刚学时看网上的讲解觉得十分头晕，似乎又有很多的乱七八糟的数组，代码又很长，省选真的考到树剖也没能敢打。现在把对树剖的一些理解写下来，毕竟刚学，理解不一定准确，也可能会有一些错误，欢迎各位大佬评论自己的见解或指出我的错误。   树链剖分，就是把树放进线段树里。既然是放在线段树里了，那么求最大值求和还有修改等等都能实现。 字面上来说，树链，是树上的路径；剖分，就是把路
【算法笔记】树链剖分
繁凡さん的博客
10-21 365
树链剖分
Aragorn 树链剖分
09-24
Aragorn 树链剖分是一种将一棵树剖分为若干条链的算法，然后利用数据结构去维护每一条链的技术。剖分完毕后，每条重链相当于一段区间，然后可以使用数据结构去维护整个树。具体过程是通过两次深度优先搜索来实现的：第一次DFS找出每个节点的子树大小和重儿子，第二次DFS连接重边形成重链。在重链上的节点使用数据结构维护，而不在当前重链上的节点，重新拉一条重链并维护。这样可以实现对树进行高效的查询和修改操作。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值