1. 前言
树链剖分,是一种树上的算法,将树划分为若干条链,然后利用线段树来处理树上信息。
在学树链剖分之前,你需要了解的知识:
- 树的基础操作以及 DFS 序。
- 线段树的基础操作。
没有学过?可以看一看我的这篇博文:线段树算法总结&专题训练1 - 倍增求解 LCA 的思路(代码不要求实现)。
没有学过?可以看一看我的这篇博文:算法学习笔记:树上最近公共祖先(LCA)
下面的所有讲解自动认为读者学过线段树的基础操作,不再赘述。
2. 详解
模板题:P3384 【模板】轻重链剖分
这篇博文的树链剖分指轻重链剖分,还有一种长链剖分也属于树链剖分,不过这个不在这篇博文的讨论范围内。
当然对于初学者可以无视上面这句话qwq。
2.1 基础定义性质
首先还是一棵树:

给出如下几个定义:
- 重儿子:在点 x x x 的所有儿子中,子树大小最大的那个儿子就是点 x x x 的重儿子,比如 3 是 1 的重儿子。如果出现多个重儿子,任取一个。
- 轻儿子:在点 x x x 的所有儿子中,不是重儿子的儿子就是轻儿子,比如 2,4 是 1 的轻儿子。
- 重边:连接点 x x x 到其重儿子的边叫做重链。
- 轻边:如果一条边不是重边,那么就是轻边。
- 重链:由若干条重边组成的链。特别的,一个孤独的叶子节点我们也认为是一条重链。 比如 8 号节点。
- 轻链:由若干条轻边组成的链。
定义有点多呀!结合下面的图理解一下吧。
红色节点表示其为重儿子,红色边表示其为重边,绿色圈表示一条重链。

这就叫做轻重链剖分,也就是通常情况下的树链剖分。
从上面的图以及定义中,我们可以归纳出这样几条性质:
- 除叶子节点之外,每个点有且仅有一个重儿子。
- 除根节点之外,每个点不是重儿子就是轻儿子。
- 每个点一定属于一条重链。
- 如果 ( u , v ) (u,v) (u,v) 是一条轻边且其字数大小不会使其被选中为重儿子,那么 s i z e v < s i z e u 2 size_v < \dfrac{size_u}{2} sizev<2sizeu。
- 从根节点到任意节点经过的轻重链个数都小于 2 log n 2\log n 2logn。
证明如下:
- 显然。叶子节点没有儿子,别的有儿子就肯定有一个重儿子。
- 显然。根节点没有父亲,只要有父亲就一定是重儿子或者轻儿子。
- 显然。只要有儿子就有重儿子,只要有重儿子就有重边,只要有重边就有重链。而不在重链上的叶子节点被单独规定过。
- ( u , v ) (u,v) (u,v) 表示 u u u 不是叶子节点,由性质 1 可以知道肯定有一个重儿子,那么如果假设 s i z e v > s i z e u 2 size_v > \dfrac{size_u}{2} sizev>2sizeu,则别的儿子节点 x x x 就肯定有 s i z e x < s i z e u 2 size_x < \dfrac{size_u}{2} sizex<2sizeu,则有 s i z e v > s i z e x size_v > size_x sizev>sizex,此时 v v v 应为重儿子, ( u , v ) (u,v) (u,v) 应为重边,矛盾。故原式得证。
- 玄学证法。
考虑一种最坏情况就是先走重边再走轻边再走重边……
不妨设先走重边,而重边的最坏情况又是直接 n − 1 n-1 n−1 个节点挂到 n n n 节点上。
那么接下来走轻边。
根据上述性质 4,走轻边的时候最坏情况就是砍半,此时变成了 n − 1 2 \dfrac{n-1}{2} 2n−1。
然后继续减一,砍半……
为什么小于 2 log n 2\log n 2logn 呢?考虑二进制证法。
砍半->右移操作,减一->减一操作。
于是证毕。终于证完了。
接下来根据上面的性质,给出一个新的定义:
- 顶端节点:一个节点的顶端节点就是他所在重链的顶端节点。
有了这些定义以及性质,接下来我们就需要确定每个点所属的重链,顶端节点等等了。
2.2 如何树链剖分
树剖的过程需要两个 dfs 来实现,写法跟 DFS 序差不多。
第一个 dfs 需要记录以下几个信息:
- 每个节点的深度 d e p [ ] dep[] dep[]。
- 每个节点的真实父亲 f a [ ] fa[] fa[]。
- 每个节点的子树大小 S i z e [ ] Size[] Size[]。
- 每个节点的重儿子 S o n [ ] Son[] Son[]。
代码:
void dfs1(int now, int father, int depth)//当前节点,父亲,深度
{
dep[now] = depth;
fa[now] = father;
Size[now] = 1;//记录所需数据
for (int i = 0; i < Next[now].size(); ++i)
{
int u = Next[now][i];
if (u == father) continue;
dfs1(u, now, depth + 1);
Size[now] += Size[u];//记录子树大小
if (Size[u] > Size[Son[now]]) Son[now] = u;//更新重儿子
}
}
第二个 dfs 需要做这样几个事情(为什么见代码后面):
- 每个节点的新编号 i d [ ] id[] id[]。
- 每个节点的新权值 v a l [ ] val[] val[]。
- 每个节点的顶端节点 T o p [ ] Top[] Top[]。
代码:
void dfs2(int now, int top_father)//当前节点与顶端节点
{
id[now] = ++cnt;//记录新编号
val[cnt] = a[now];//新的权值
Top[now] = top_father;//顶端节点
if (!Son[now]) return ;
dfs2(Son[now], top_father);//先遍历重儿子
for (int i = 0; i < Next[now].size(); ++i)
{
int u = Next[now][i];
if (u == fa[now] || u == Son[now]) continue;
dfs2(u, u);//遍历轻儿子
}
}
注意写代码时的注意点:
- 要先遍历重儿子。
- 遍历轻儿子的时候注意更新 t o p _ f a t h e r top\_father top_father
那么为什么要先遍历重儿子?有什么好处吗?
好处就是:一条重链上的所有节点编号是连续的。
比如还是这棵树。

如果我们在 dfs 时先走重儿子,再走轻儿子,编号之后如下(蓝色为新编号):
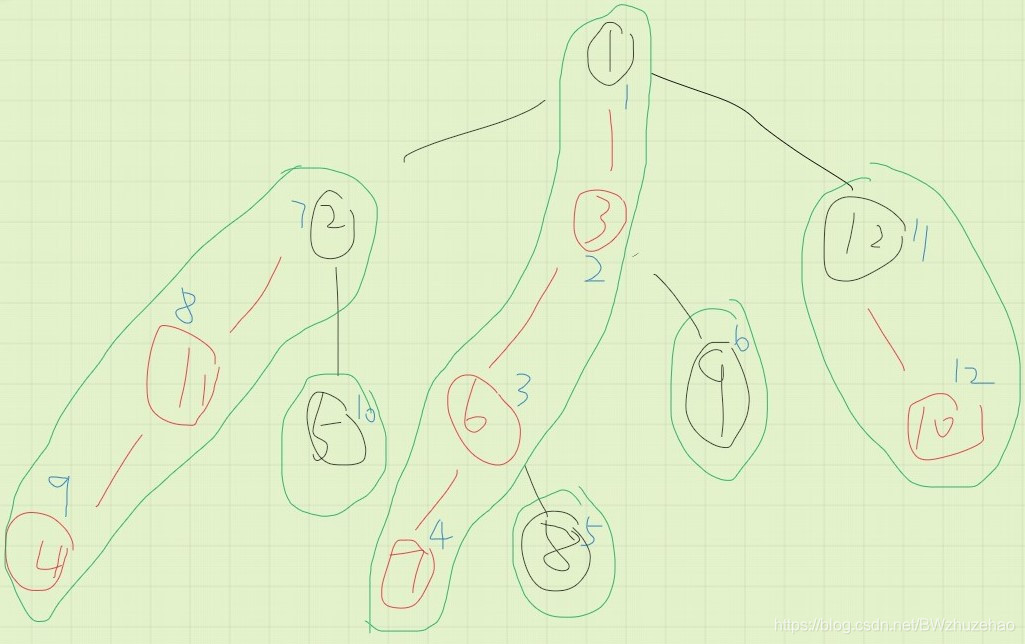
从图上可以很清晰的看出来:
- 定理一:重链上的点编号连续。
- 定理二:任意节点的子树内部编号连续。
证明如下:
- 因为遍历方式为先走重边,所以一条重链上的点一定是一直走下去的。
- 这是 DFS 序的基本性质。
编号连续有什么好处吗?
这样就可以使用线段树来维护一条重链上的信息。
我们在区间 [ 1 , n ] [1,n] [1,n] 上建一棵线段树,将 新树 的信息存到线段树里面,这样因为一条重链上编号连续,就可以使用线段树在 O ( log n ) O(\log n) O(logn) 的时间复杂度内解维护以及查询。
线段树的所有操作存在 namespace Segment_tree 里面。
对应函数名,变量名以及功能如下:
| 函数名 | 作用 |
|---|---|
| build | 建树 |
| spread | 下压 lazy_tag |
| add | 区间加 |
| ask | 区间查询 |
| l ( p ) , r ( p ) l(p),r(p) l(p),r(p) | p p p 节点所维护区间的左右端点 |
| s ( p ) , a ( p ) s(p),a(p) s(p),a(p) | p p p 节点的区间和与 lazy_tag |
接下来考虑操作。
2.3 对于路径操作
题中对于路径 x − > y x->y x−>y 操作有两个:区间加,区间查询。
这个时候就要分情况讨论了。规定 x x x 深度大于 y y y。
- 如果 x , y x,y x,y 在一条重链上,那么直接区间修改/区间查询 i d x , i d y id_x,id_y idx,idy 即可,判定方法为看顶端节点是否相同。
- 如果 x , y x,y x,y 不在一条重链上,此时我们要想办法让 x , y x,y x,y 在一条重链上,最简单的方法就是区间修改/区间查询 i d t o p x , i d x id_{top_x},id_x idtopx,idx,然后让 x x x 跳到 f a t o p x fa_{top_x} fatopx。重复上述步骤。
正确性证明:
- 首先区间修改/区间查询 i d t o p x , i d x id_{top_x},id_x idtopx,idx 的时候,根据定理一,保证重链上的编号连续。
- 因为令 x x x 跳到 f a t o p x fa_{top_x} fatopx 上,此时不仅保证不重复,而且此时会换一条重链操作,最坏情况就是跳到根节点。
- 那么怎么保证时间复杂度呢?还记得之前有证明过一个结论吗:从根节点到任意节点经过的轻重链个数都小于 2 log n 2\log n 2logn。根据这个结论,复杂度即为 log \log log 级别。
代码:
void add1(int x, int y, LL k)
{
while (Top[x] != Top[y])//控制顶端节点
{
if (dep[Top[x]] < dep[Top[y]]) std::swap(x, y);//保证 x 深度较大
Segment_tree::add(1, id[Top[x]], id[x], k);//区间修改
x = fa[Top[x]];//跳
}
if (dep[x] > dep[y]) std::swap(x, y);//剩余部分处理
Segment_tree::add(1, id[x], id[y], k);
}
LL ask1(int x, int y)
{
LL ans = 0;
while (Top[x] != Top[y])//控制顶端节点
{
if (dep[Top[x]] < dep[Top[y]]) std::swap(x, y);//保证 x 深度较大
ans = (ans + Segment_tree::ask(1, id[Top[x]], id[x])) % P;//区间修改
x = fa[Top[x]];//跳
}
if (dep[x] > dep[y]) std::swap(x, y);//剩余部分处理
ans = (ans + Segment_tree::ask(1, id[x], id[y])) % P;
return ans;
}
2.4 对于子树操作
根据定理二,字数内节点编号连续,这样直接在线段树上对 [ i d x , i d x + S i z e x − 1 ] [id_x,id_x+Size_x-1] [idx,idx+Sizex−1] 操作即可。
代码:
void add2(int x, LL k)
{
Segment_tree::add(1, id[x], id[x] + Size[x] - 1, k);
}
LL ask2(int x)
{
return Segment_tree::ask(1, id[x], id[x] + Size[x] - 1) % P;
}
2.5 时空复杂度分析
对于时间复杂度:
两遍 dfs 时间复杂度为 O ( n ) O(n) O(n)。
线段树建树时间复杂度为 O ( n log n ) O(n \log n) O(nlogn)。
对于路径操作,单次操作时间复杂度为树剖复杂度 O ( log n ) O(\log n) O(logn) 乘上线段树复杂度 O ( log n ) O(\log n) O(logn),即为 O ( log 2 n ) O(\log^2 n) O(log2n)。
对于子树操作,单次操作时间复杂度为 O ( log n ) O(\log n) O(logn)。
考虑最坏情况下都是路径操作,那么总复杂度为 O ( m log n ) O(m \log n) O(mlogn)。
n , m n,m n,m 同阶,则为 O ( n log 2 n ) O(n \log^2 n) O(nlog2n)。
关于空间复杂度:
线段树 O ( n ) O(n) O(n),各类辅助数组 O ( n ) O(n) O(n),总复杂度 O ( n ) O(n) O(n)。
但是!树剖会被卡。
确实树剖在大多数情况下表现良好,但是树剖常数大的话是可以被『有理有据』的卡掉的。
『有理有据的卡树剖』详见 OI-wiki 怎么有理有据的卡树剖
2.6 代码
代码:
/*
========= Plozia =========
Author:Plozia
Problem:P3384 【模板】轻重链剖分
Date:2021/3/7
========= Plozia =========
*/
#include <bits/stdc++.h>
using std::vector;
typedef long long LL;
const int MAXN = 1e5 + 10;
int n, m, root, P, fa[MAXN], Son[MAXN], dep[MAXN], a[MAXN], cnt, Size[MAXN];
int id[MAXN], Top[MAXN], val[MAXN];
vector <int> Next[MAXN];
struct node
{
int l, r;
LL sum, add;
#define l(p) tree[p].l
#define r(p) tree[p].r
#define s(p) tree[p].sum
#define a(p) tree[p].add
}tree[MAXN << 2];
int read()
{
int sum = 0, fh = 1; char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
return (fh == 1) ? sum : -sum;
}
namespace Segment_tree
{
void build(int p, int l, int r)
{
l(p) = l, r(p) = r;
if (l == r) {s(p) = val[l]; return ;}
int mid = (l + r) >> 1;
build(p << 1, l, mid); build(p << 1 | 1, mid + 1, r);
s(p) = (s(p << 1) + s(p << 1 | 1)) % P;
}
void spread(int p)
{
if (a(p))
{
s(p << 1) = (s(p << 1) + ((LL)r(p << 1) - l(p << 1) + 1) * a(p)) % P;
s(p << 1 | 1) = (s(p << 1 | 1) + ((LL)r(p << 1 | 1) - l(p << 1 | 1) + 1) * a(p)) % P;
a(p << 1) += a(p); a(p << 1 | 1) += a(p); a(p) = 0;
}
}
void add(int p, int l, int r, LL k)
{
if (l(p) >= l && r(p) <= r)
{
s(p) = (s(p) + k * (r(p) - l(p) + 1)) % P;
a(p) += k; return ;
}
spread(p);
int mid = (l(p) + r(p)) >> 1;
if (l <= mid) add(p << 1, l, r, k);
if (r > mid) add(p << 1 | 1, l, r, k);
s(p) = (s(p << 1) + s(p << 1 | 1)) % P;
}
LL ask(int p, int l, int r)
{
if (l(p) >= l && r(p) <= r) return s(p);
spread(p); int mid = (l(p) + r(p)) >> 1; LL ans = 0;
if (l <= mid) ans += ask(p << 1, l, r);
if (r > mid) ans += ask(p << 1 | 1, l, r);
return ans % P;
}
}
void dfs1(int now, int father, int depth)//当前节点,父亲,深度
{
dep[now] = depth;
fa[now] = father;
Size[now] = 1;//记录所需数据
for (int i = 0; i < Next[now].size(); ++i)
{
int u = Next[now][i];
if (u == father) continue;
dfs1(u, now, depth + 1);
Size[now] += Size[u];//记录子树大小
if (Size[u] > Size[Son[now]]) Son[now] = u;//更新重儿子
}
}
void dfs2(int now, int top_father)//当前节点与顶端节点
{
id[now] = ++cnt;//记录新编号
val[cnt] = a[now];//新的权值
Top[now] = top_father;//顶端节点
if (!Son[now]) return ;
dfs2(Son[now], top_father);//先遍历重儿子
for (int i = 0; i < Next[now].size(); ++i)
{
int u = Next[now][i];
if (u == fa[now] || u == Son[now]) continue;
dfs2(u, u);//遍历轻儿子
}
}
void add1(int x, int y, LL k)
{
while (Top[x] != Top[y])//控制顶端节点
{
if (dep[Top[x]] < dep[Top[y]]) std::swap(x, y);//保证 x 深度较大
Segment_tree::add(1, id[Top[x]], id[x], k);//区间修改
x = fa[Top[x]];//跳
}
if (dep[x] > dep[y]) std::swap(x, y);//剩余部分处理
Segment_tree::add(1, id[x], id[y], k);
}
LL ask1(int x, int y)
{
LL ans = 0;
while (Top[x] != Top[y])//控制顶端节点
{
if (dep[Top[x]] < dep[Top[y]]) std::swap(x, y);//保证 x 深度较大
ans = (ans + Segment_tree::ask(1, id[Top[x]], id[x])) % P;//区间修改
x = fa[Top[x]];//跳
}
if (dep[x] > dep[y]) std::swap(x, y);//剩余部分处理
ans = (ans + Segment_tree::ask(1, id[x], id[y])) % P;
return ans;
}
void add2(int x, LL k)
{
Segment_tree::add(1, id[x], id[x] + Size[x] - 1, k);
}
LL ask2(int x)
{
return Segment_tree::ask(1, id[x], id[x] + Size[x] - 1) % P;
}
int main()
{
n = read(), m = read(), root = read(), P = read();
for (int i = 1; i <= n; ++i) a[i] = read() % P;
for (int i = 1; i < n; ++i)
{
int x = read(), y = read();
Next[x].push_back(y), Next[y].push_back(x);
}
dfs1(root, root, 1); dfs2(root, root);
Segment_tree::build(1, 1, n);
for (int i = 1; i <= m; ++i)
{
int opt = read();
if (opt == 1)
{
int x = read(), y = read(), z = read() % P;
add1(x, y, z);
}
if (opt == 2)
{
int x = read(), y = read();
printf("%lld\n", ask1(x, y) % P);
}
if (opt == 3)
{
int x = read(), z = read() % P;
add2(x, z);
}
if (opt == 4)
{
int x = read();
printf("%lld\n", ask2(x) % P);
}
}
return 0;
}
3. 练习题
练习题传送门:树链剖分算法总结&专题训练























 122
122











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








