图算法-最大流

1. 最大流问题描述

流网络：

源结点 s,汇点 t,每个结点都在从源结点到汇点的某条路径上

流网络G中的流 是一个实值函数f: V * V -> R

流满足两条性质：

(流量守恒：流入结点的总流量等于流出结点的总流量(除源结点与汇点以外))

流 f 的值 | f |

即从源结点流出的总流量减去流入源结点的总流量

最大流问题 ：给定一个流网络G、一个源结点、一个汇点，求值最大的流

2.Ford-Fulkerson方法

残存网络 G_f由特定流网络G与流f产生

残存容量c_f(u,v):

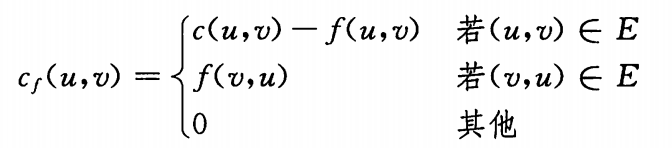
理解: 图G中，若存在残存流量的边加入图G_f, 同时对不存在残存流量的边，将反向流量加入图G_f中

注： 残存网络并不是流网络，因不满足流网络的定义(可能同时存在双向的边)

举例:

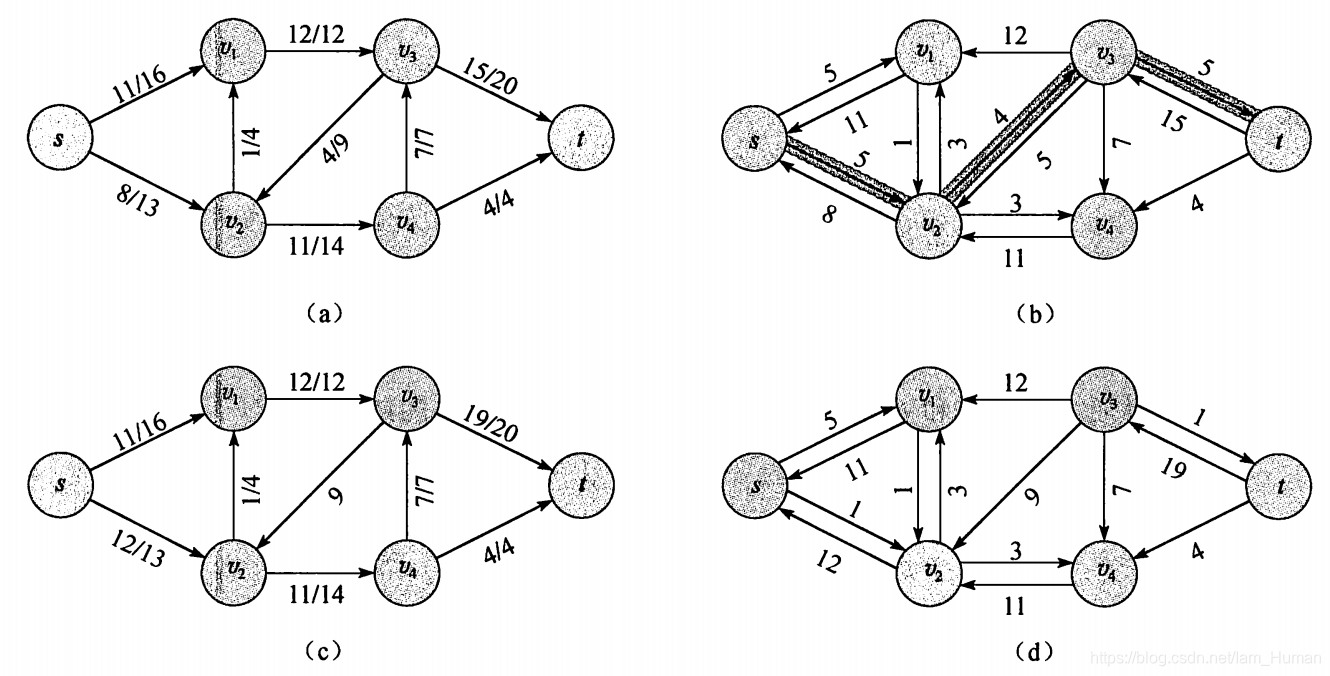
(左边是流网络，右边是残存网络)

如果f是G中的一个流，f’是对应残存网络G_f中的一个流， 定义f | f’为流f’对流f的递增， 它是一个V*V->R的函数：

引理：

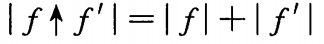
增广路径

对流网络G=(V, E)和流f, 增广路径p是残存网络G_f中一条从源结点s到汇点t的简单路径。
称在一条增广路径p上能够为每条边增加的流量的最大值为路径p的残存容量，定义：

关于(由增广路径诱导的流网络G中的流f)f_p定义如下：

将流f增加f_p的量， 将获得G中另一个流， 该流的值更加接近最大流

3.最小割

流网络的切割
流网络G=(V, E)中的一个切割(S, T)将结点集合V划分为S和T=V-S两个集合，使得s属于S，t属于T

若f是一个流，则定义横跨切割(S, T)的净流量 f(S, T)如下：

切割(S, T)的容量是

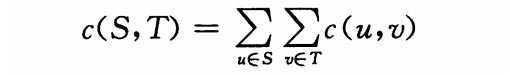
一个网络的最小切割是整个网络中容量最小的切割

举例：

1. 对网络的一个流f, 网络的任意切割(S, T)都有切割的净流量等于流f的值，即f(S, T) = | f |
2. 流网络G中的任意流f的值都不能超过G中任意切割的容量，即 max | f | <= min c(S, T)

4.最大流最小割定理

求最大流/最小割： Ford-Fulkerson方法
基本的Ford-Fulkerson算法：

举例：

算法时间复杂度分析：
运行时间取决于第三行如何寻找增广路径，如果选择不好，流的值回随着递增而增加，但不一定收敛于最大值。

1. 容量值为整数(或有理数)且最大流值较小
   如果容量是有理数，可通过乘以系数转换为整数，设f* 为转换后网络的最大流
   通过深度优先搜索或广度优先搜索，在残存网络中找到一条路径的时间为O(V+E’) = O(E), while的每次循环所需时间为O(E), 流量值每次迭代最少增加一个单位，因此总的算法运行时间为 O(E |f|)*

2. |f*|取值很大的特殊情况–Edmonds-Karp算法
   
   在残存网络中选择增广路径是一条从源结点到汇点的最短路径

#include<cstdio>
#include<cstring>
#include<vector>
#include<iostream>
#include<algorithm>
# define maxflowLimit 10000
# define NumofVLimit 505

//最大流最大不能超过maxflowLimit
//结点数最多不超过NumofVLimit
//源结点编号必须为1， 汇点编号必须为n+1
//举例：
//6 9
//1 2 16
//1 3 13
//3 2 4
//2 4 12
//3 5 14
//4 3 9
//5 4 7
//4 6 20
//5 6 4
//
//the max flow is 23
//the number of S about min ge is 4
//1 2 3 5

using namespace std;
struct node{
    int to,w,vap;
}Q;

int n,m,shu;         //n:结点个数  m:边的个数
bool fafe[NumofVLimit];      //fafe:  记录结点是否被访问
vector<node> V[NumofVLimit]; //邻接表 存储图， 向量便于深度优先搜索


void add_edge(int a,int b,int c)
{
    Q.to=b;Q.w=c;Q.vap=V[b].size();
    V[a].push_back(Q);                // a->b  容量为c   size：与之连通的结点数，容量0不算
    Q.to=a;Q.w=0;Q.vap=V[a].size()-1; // b->a  容量为0
    V[b].push_back(Q);
}

int ex_dfs(int x,int mi)   //使用深度优先搜索 找到从结点a开始的增广路径，返回该增广路径的容量
{
    fafe[x]=true;
    if (x==n) return mi;
    for (int i=0;i<V[x].size();i++)
    {
        if (fafe[V[x][i].to]||V[x][i].w==0) continue;  //递归出口1： 该点被访问过 或 至该店路径值为0
        int k=ex_dfs(V[x][i].to,min(mi,V[x][i].w));
        if (k)  //递归出口2  k=0
        {
            V[x][i].w-=k;  // <2, 4> - 1
            V[V[x][i].to][V[x][i].vap].w+=k; //<4, 2> + 1 这里的vap=0是2在V[4]里的位置，不是指代2
            return k;
        }
    }
    return 0;
}

void dfs_(int x,int lei)  //在最后的残存网络上，通过深度优先搜索， 寻找最小割，将原点能到达的结点与源结点划为一个集合
{
    fafe[x]=true;shu++;
    if (lei==1)
        printf("%d%c",x,m==shu?'\n':' ');
    for (int i=0;i<V[x].size();i++)
    {
        if (fafe[V[x][i].to]||V[x][i].w==0) continue;
        dfs_(V[x][i].to,lei);
    }
}

int main()
{
    printf("Please input the number of V and the number of E\n");
    scanf("%d%d",&n,&m);  //n:节点个数  m:边的个数
    int a,b,c;
    while (m--)
    {
        scanf("%d%d%d",&a,&b,&c);   //依次输入各边<a, b>  边的权值为c,  源结点必须为1
        add_edge(a,b,c);
    }
    int ans=0;a=1;
    while (a)
    {
        a=0;
        memset(fafe,false,sizeof(fafe));
        a=ex_dfs(1,maxflowLimit);   //迭代从源结点开始探索增广路径， a是增广路径的容量， 直到a为0，即不再存在增广路径
        ans+=a; //ans依次累加增广路径的残存容量， 最终即为最大流值
    }
    memset(fafe,false,sizeof(fafe));
    shu=0;dfs_(1,0);m=shu;       //计算m = shu,即最小割中S集合的结点数
    memset(fafe,false,sizeof(fafe));
    printf("the max flow is %d\n",ans);
    printf("the number of S about min ge is %d\n", m);
    shu=0;dfs_(1,1);            //输出最小割中S集合的各个结点
    return 0;
}