数据结构与算法——二叉树遍历实现

遍历Traverse：就是按照某种次序访问所有节点，且每个节点恰好访问一次。

树的遍历可以看成是人为的将非线性结构线性化

---

将树看成三个部分：左子树、右子树、根

遍历的方法三种：

1. 先序DLR：根、左子树、右子树
2. 中序LDR：左子树、根、右子树
3. 后序LRD：左子树、右子树、根

采用了递归的思路

---

面试题:有一个二叉树，它的后序遍历序列为5 4 3 7 6 2 1，中序遍历的序列为4 5 1 3 2 6 7，则其先序遍历的序列是什么？

先序：1452367

---

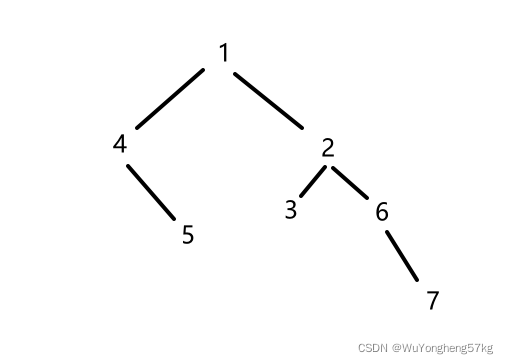
实现：

先创建一棵二叉树

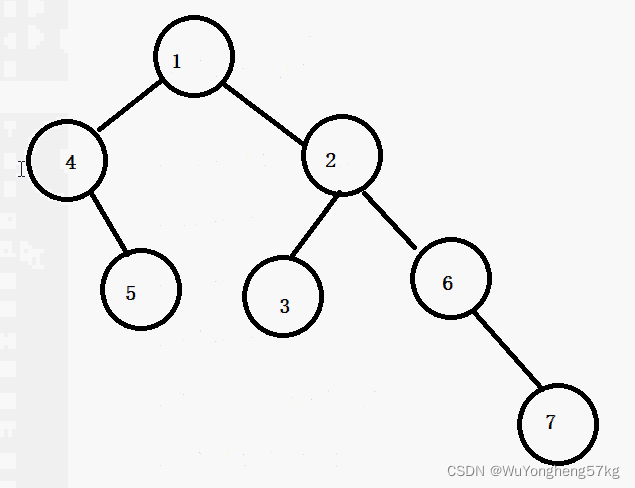
        Node node5 = new Node(5, null, null);
        Node node4 = new Node(4, null, node5);
        Node node3 = new Node(3, null, null);
        Node node7 = new Node(7, null, null);
        Node node6 = new Node(6, null, node7);
        Node node2 = new Node(2, node3, node6);
        Node node1 = new Node(1, node4, node2);

        BinaryTree bTree = new LinkedBinaryTree(node1);

 先序遍历

public void perOrderTraverse() {
        //输出根节点的值
        if (root != null) {
            System.out.print(root.value + " ");
            //对左子树进行先序遍历
            BinaryTree leftTree = new LinkedBinaryTree(root.leftChild);
            leftTree.perOrderTraverse();
            //对右子树进行先序遍历
            BinaryTree rightTree = new LinkedBinaryTree(root.rightChild);
            rightTree.perOrderTraverse();
        }
    }

中序遍历

    @Override
    public void inOrderTraverse(Node node) {
        if (node != null) {
            // 遍历左子树
            this.inOrderTraverse(node.leftChild);
            //输出根的值
            System.out.print(node.value + " ");
            // 遍历右子树
            this.inOrderTraverse(node.rightChild);
        }
    }

得到树的高度

思路：递归，左子树和右子树中找大的，再加上根（加1）

@Override
    public int getHeight() {
        System.out.println("二叉树的高度是");
        return this.getHeight(root);
    }

    private int getHeight(Node node) {
        if (node == null) {
            return 0;
        } else {
            // 获取左子树的高度
            int nleft = this.getHeight(node.leftChild);
            // 获取右子树的高度
            int nright = this.getHeight(node.rightChild);
            // 返回左子树，右子树较大的值并加1
            return nleft > nright ? nleft + 1 : nright + 1;
        }
    }

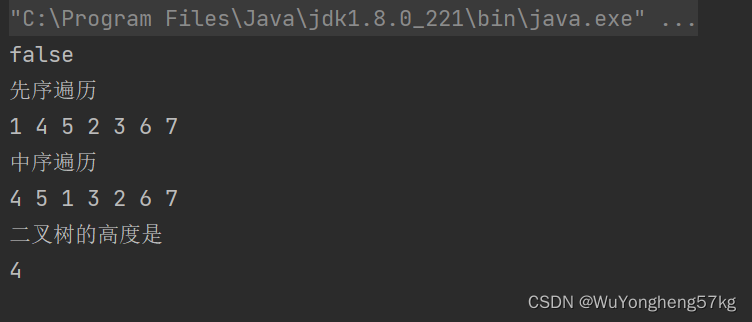
计算二叉树节点数量

    @Override
    public int size() {
        System.out.print("二叉树的节点数为:");
        return this.size(root);
    }

    private int size(Node node) {
        if (node == null) {
            return 0;
        } else {
            // 获取左子树的size
            int nleft = this.size(node.leftChild);
            // 获取右子树的size
            int nright = this.size(node.rightChild);
            // 返回左子树，右子树较大的值并加1
            return nleft + nright + 1;

        }
    }

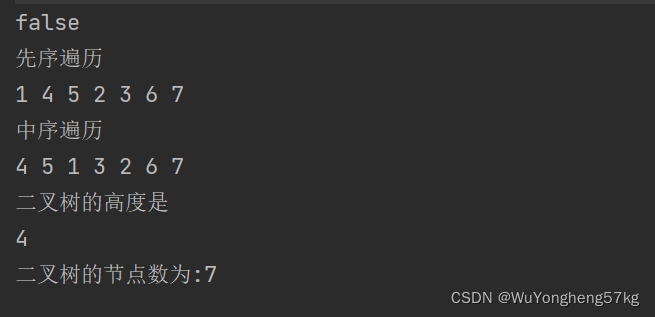
在二叉树查找某个值

思路：递归 ，在某个根节点下进行查找

@Override
    public Node findKey(int value) {
        return this.findKey(value, root);
    }

    private Node findKey(Object value, Node node) {
        /*
        * 节点为空，可能是整个数的根节点，也可能是叶子节点
        */
        if (node == null) {
            return null;
        } else if (node != null && node.value == value) { // 递归接收条件，如果找到就结束递归
            return node;
        } else {
            Node node1 = this.findKey(value, node.leftChild);
            Node node2 = this.findKey(value, node.rightChild);
            if (node1 != null && node1.value == value) {
                return node1;
            } else if (node2 != null && node2.value == value) {
                return node2;
            }else {
                return null;
            }
        }
    }

按层次遍历

思路：不能用递归，借助队列

 @Override
    public void levelOrderBystack() {
        System.out.println("按照层次遍历二叉树");
        if (root == null) {
            return;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);// 先把根放入队列
        while (queue.size() != 0) {
            int len = queue.size();
            for (int i = 0; i < len; i++) {
                Node temp=queue.poll();// 出队
                // 根出队后，会把根的左右孩子放入队列
                System.out.print(temp.value+" ");
                if (temp.leftChild!=null){
                    queue.add(temp.leftChild);
                }
                if (temp.rightChild!=null){
                    queue.add(temp.rightChild);
                }
            }
        }
        System.out.println();
    }