基尼不纯度:从一个数据集中随机选取子项,度量其被错误的划分到其他组里的概率。(书上解释)
一个随机事件变成它的对立事件的概率(简单理解)
计算公式:(fi为某概率事件发生的概率)
下图是相关曲线图,可以参考数据挖掘导论的98页:
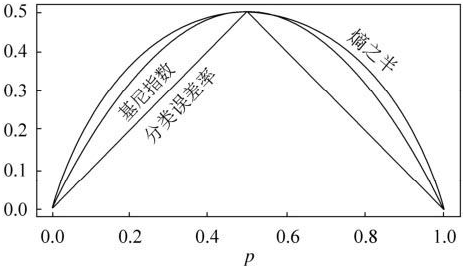
从上图可以看出,基尼系数和熵之半的曲线非常接近,仅仅在45度角附近误差稍大。因此,基尼系数可以做为熵模型的一个近似替代。
讲解案例:
一个随机事件X ,P(X=0)= 0.5 ,P(X=1)=0.5
那么基尼不纯度就为 P(X=0)*(1 - P(X=0)) + P(X=1)*(1 - P(X=1)) = 0.5
一个随机事件Y ,P(Y=0)= 0.1 ,P(Y=1)=0.9
那么基尼不纯度就为P(Y=0)*(1 - P(Y=0)) + P(Y=1)*(1 -P(Y=1)) = 0.18
很明显 X比Y更混乱,因为两个都为0.5 很难判断哪个发生。而Y就确定得多,Y=1发生的概率很大。而基尼不纯度也就越小。
结论:
(1)基尼不纯度可以作为 衡量系统混乱程度的 标准;
(2)基尼不纯度越小,纯度越高,集合的有序程度越高,分类的效果越好;
(3)基尼不纯度为 0 时,表示集合类别一致;
(4)在决策树中,比较基尼不纯度的大小可以选择更好的决策条件(子节点)。
Python3示例代码:
#示例代码:
my_data = [['fan', 'C', 'yes', 32, 'None'],
['fang', 'U', 'yes', 23, 'Premium'],
['ming', 'F', 'no', 28, 'Basic']]
# 计算每一行数据的可能数量
def uniqueCounts(rows):
results = {}
for row in rows:
# 对最后一列的值计算
#r = row[len(row) - 1]
# 对倒数第三的值计算,也就是yes 和no 的一列
r = row[len(row) - 3]
if r not in results: results[r] = 0
results[r] += 1
return results
# 基尼不纯度样例
def giniImpurityExample(rows):
total = len(rows)
print(total)
counts = uniqueCounts(rows)
print(counts)
imp = 0
for k1 in counts:
p1 = float(counts[k1]) / total
print(counts[k1])
for k2 in counts:
if k1 == k2: continue
p2 = float(counts[k2]) / total
imp += p1 * p2
return imp
gini = giniImpurityExample(my_data)
print('gini Impurity is %s' % gini)







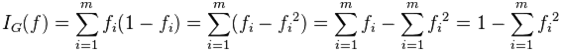















 2022
2022











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










