零钱系统（基于贪心算法）实验报告

1、题目陈述

        假设零钱系统的币值是{1,p,p^2,...,p^n}，p>1，且每个钱币的重量都等于1，设计一个最坏情况下时间复杂度最低的算法，使得对任何钱数y，该算法得到的零钱个数最少，说明算法的主要设计思想，证明它的正确性，并给出最坏情况下的时间复杂度。

2、设计思想

        题目的目标翻译过来就是要最小化找回零钱时所需的硬币数量。给定硬币的面额是1,p,p^2,...,p^n，并且p是一个大于1的整数，那么n就决定了最大的硬币面额。问题的关键就在于该如何有效地分配这些不同面额的硬币，以达到最少硬币数目的目的。

        显然，这里一个比较好的选择是使用贪心策略。贪心策略的核心思想简单来说可以总结如下：在每一步选择中都采取局部最优解，期望通过一系列局部最优的选择达到全局最优解。

        这个思想在某些问题中并不能达到最优结果，例如背包问题就不太好用贪心法来解决；但对于本问题来说，“局部最优”意味着每次将优先选取当前能够使用的最大面额的硬币，换言之，较大面额的硬币使用得越多，总体需要的硬币数自然越少——符合题意。

        下面用伪代码来整理一下思路。

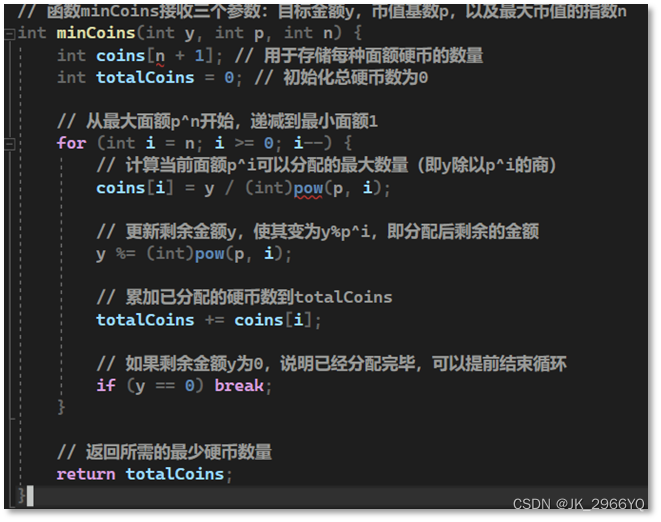
        这里定义一个名为minCoins的函数，它接收三个参数：目标找零金额TATGET_AMOUNT y，币值的基数BASE p，以及最大币值的指数MAX_EXXPONENT n。之后我们初始化一个数组coins来记录使用的每个面额硬币的数量，数组的长度为n+1，以覆盖从1到p^n所有可能的面额。接着，定义一个变量totalCoins来累计所需要的总硬币数，初始化为0。

        随后我们使用一个从n递减到0的循环，这可以使得我们按照硬币面额从大到小进行处理。在循环内部，首先计算并存储当前面额p^i可以分配的最大数量，即目标金额y除以p^i并向下取整。之后需要更新剩余金额y，通过取模运算得到分配完当前面额后剩余的金额，随后将当前已分配的硬币数累加到totalCoins中。如果在某次迭代之后剩余金额y变成了0，说明已经分配完了所有的金额，此时就可以break出循环，因为没有必要继续检查更小的面额了。最后函数返回累计的最少硬币数totalCoins。

        具体用C语言编写如下：

        举个例子来更好地理解。

        假设我们要找零y=255元，硬币面额为1，2，4，8，16，32，64，即p=2,n=6。

        从最大面额64元开始，255/64 = 4……7，即可以使用4个64元硬币，剩下7元；

        接下来是32元，7/32 = 0……7，剩下7元不变；

        然后是16元，7/16 = 0……7，剩下7元不变；

        8元，7/8 = 0……7，剩下7元不变；

        4元，7/4 = 1……3，使用1个4元硬币，剩下3元；

        2元，3/2 = 1……1，使用1个2元硬币，剩下1元；

        最后是1元，剩下的1元正好使用1元硬币。

        总共使用了6枚硬币，这就是用贪心法得到的最少的硬币数。

3、时间复杂度

        主要对minCoins函数进行分析。

        1、初始化数组和计数器

        这一步是常数时间操作，时间复杂度为O(1)。

        2、循环

        主要的循环是从n递减到0，共执行n+1次，在这个循环里：

        （1）计算硬币数量：

        使用y / (int)pow(p, i)计算最大可分配的硬币数量，pow函数的时间复杂度通常为O(log n)，但在这种情况下，因为总是计算p的幂（p^i），并且i的范围是从n到0，p是一个常数，实际操作中计算p^i可以优化，例如通过重复平方的方式在O(log i)时间内完成，但在这个函数中，考虑到i的范围有限且固定，这部分可以视为常数时间操作或低阶项，尤其是在实际编程中可能直接通过移位操作实现幂运算，故简化理解为O(1)。

        （2）更新剩余金额：

        y %= (int)pow(p, i)操作的时间复杂度也是O(1)。

        （3）累加硬币数：

        将硬币数量加到totalCoins上的操作是O(1)。

        （4）检查退出条件：

        if (y == 0) break;也是O(1)。

        综合上述分析，循环内的每个操作都是常数时间，但循环本身会执行n+1次。因此，循环部分的时间复杂度是O(n)。所以整个minCoins函数的时间复杂度主要由循环决定，即O(n)，其中，n是最大币值的指数。这意味着算法的执行时间与问题规模（即硬币面额的最大指数）成线性关系，不直接依赖于目标金额y的具体大小，因此对于非常大的y值，算法依然保持高效。

4、可行性分析

        这个算法之所以可以使用贪心策略，是因为它解决的问题——找零问题，满足贪心算法适用的特定条件。

1、贪心选择性质：在找零问题中，每一步选择当前面额最大的硬币（在不超过剩余找零金额的前提下）是局部最优的。这是因为使用更大面额的硬币可以更快减少剩余金额，从而最小化硬币的总数。这个选择不会影响未来决策的最优性，因为每一步我们都尽可能减少了剩余的找零金额，且不会导致未来无法使用更小面额的硬币完成找零。

2、最优子结构：找零问题可以分解为更小子问题。一旦决定使用了一个硬币，剩余的找零问题成为一个规模更小的相同问题，我们可以递归地应用同样的贪心策略。即，对于任何子问题，其最优解也是由当前最优选择加上对剩余金额的最优解组成的。

3、无后效性：在找零过程中，一旦选择了某面额的硬币，之后的选择不会受到这个选择的影响，因为我们总是基于当前剩余金额做出最佳选择。换句话说，我们不需要撤销或更改之前的决策，因为当前的决策只依赖于当前的剩余金额，与过去的决策无关。

4、硬币面额的特殊性：在这个问题中，硬币面额是1, p, p^2, ..., p^n的形式，这是一个几何序列。这样的序列保证了每次选择最大可使用的硬币后，剩余的金额仍然能够被后续的硬币面额整除，避免了因硬币不可分割导致的局部最优选择不能导出全局最优解的问题。这与一般找零问题不同，一般找零可能不满足贪心条件，比如面额为{1, 3, 4}时，贪心选择不一定能得到最优解。

        综上所述，由于找零问题具有贪心选择性质、最优子结构和无后效性，且硬币面额的特殊排列方式允许我们安全地做出局部最优选择而不影响全局最优性，因此贪心算法成为解决这个问题的有效策略。