在吴恩达深度学习视频以及大树先生的博客提炼笔记基础上添加个人理解,原大树先生博客可查看该链接地址大树先生的博客- ZJ
CSDN:http://blog.csdn.net/junjun_zhao/article/details/79226016
第二周 神经网络基础 (Basics of Neural Network Programming )
2.1 二分分类 ( Binary Classification)
神经网络编程的基础知识
例如 m 个样本的训练集,你可能会习惯性地去用一个 for 循环,来遍历这 m 个样本。实现一个神经网络,如果你要遍历整个训练集,并不需要直接使用 for 循环。
本周介绍为什么神经网络的计算过程可以分为 前向传播和反向传播 两个分开的过程。 用logistic 回归 来阐述,以便于更好地理解。
logistic 回归是一个用于二分分类的算法。
二分分类问题的例子:
假如你有一张图片作为输入,这样子的,你想输出识别此图的标签,如果是猫 输出 1,如果不是 则输出 0,我们用 y 来表示输出的结果标签。
一张图片在计算机中的表示:
三个独立矩阵,分别对应图片中的 红、绿、蓝三个颜色通道,如果输入图片是 64×64 像素的,就有三个 64×64 的矩阵,分别对应图片中 红、绿、蓝 三种像素的亮度。放入一个特征向量 x x 。 向量 x 的总维度 就是 64×64×3=12288
Notation 符号
- 样本:,训练样本包含 m 个;
- 其中 x∈Rnx x ∈ R n x ,表示样本 x 包含 nx n x 个特征;
- y∈0,1 y ∈ 0 , 1 ,目标值属于 0、1分类;
- 训练数据: {(x(1),y(1)),(x(2),y(2)),⋯,(x(m),y(m))} { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋯ , ( x ( m ) , y ( m ) ) }
训练数据样本形状: X.shape=(nx,m) X . s h a p e = ( n x , m )
对应标签数据的形状: Y=[y(1),y(2),⋯,y(m)] Y = [ y ( 1 ) , y ( 2 ) , ⋯ , y ( m ) ] , Y.shape=(1,m) Y . s h a p e = ( 1 , m )
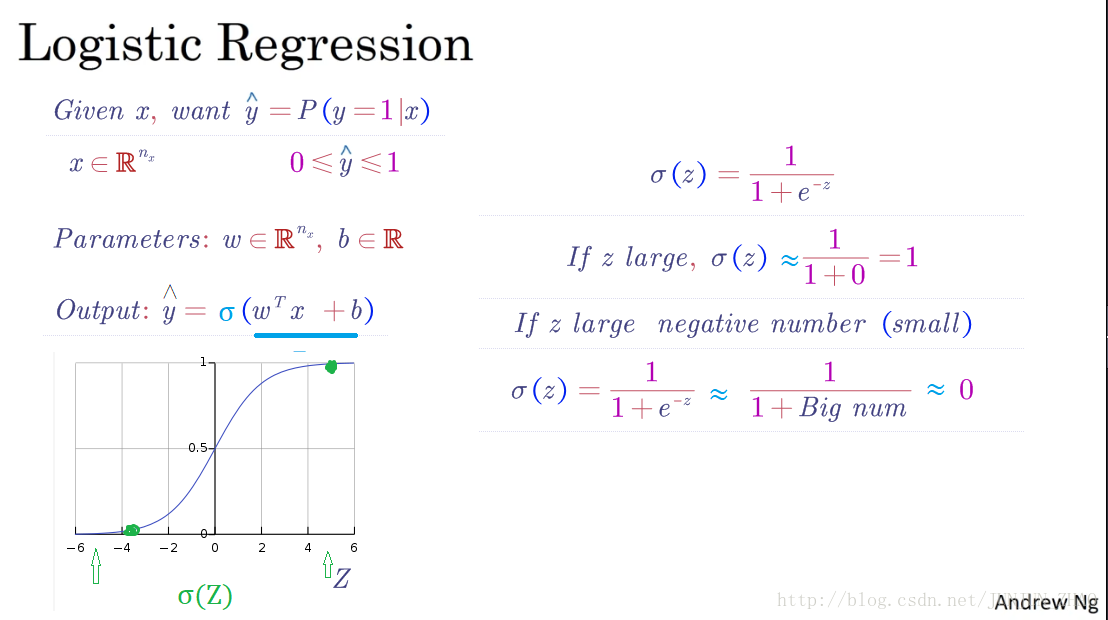
2.2 Logistic 回归 (Logistic Regression)
logistic 回归,用在监督学习问题中的学习算法 ,输出 y 标签是 0 或 1 ,这是一个二元分类问题
逻辑回归中,预测值:
h^=P(y=1|x) h ^ = P ( y = 1 | x ) 其表示为 1 的概率,取值范围在 [0,1] 之间。
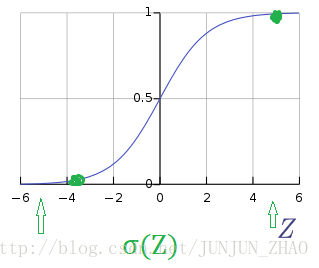
引入 Sigmoid 函数,预测值:
y^=Sigmoid(wTx+b)=σ(wTx+b) y ^ = S i g m o i d ( w T x + b ) = σ ( w T x + b ) 其中
Sigmoid(z)=11+e−z S i g m o i d ( z ) = 1 1 + e − z 注意点:函数的一阶导数可以用其自身表示,
该部分的求导可查看:Logistic回归-代价函数求导过程 | 内含数学相关基础
σ′(z)=σ(z)(1−σ(z)) σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) ) 这里可以解释梯度消失的问题,当 z=0 z = 0 时,导数最大,但是导数最大为 σ′(0)=σ(0)(1−σ(0))=0.5(1−0.5)=0.25 σ ′ ( 0 ) = σ ( 0 ) ( 1 − σ ( 0 ) ) = 0.5 ( 1 − 0.5 ) = 0.25 ,这里导数仅为原函数值的 0.25 倍。
2.3 Logistic 回归成本函数 (Logistic Regression Cost function)
logistic 回归的模型,为了训练 logistic 回归模型的参数 w 以及 b,需要定义一个成本函数,用 logistic 回归来训练的成本函数。
让模型来通过学习调整参数:
- m 个样本的训练集, 通过在训练集 找到参数 w 和 b ,得到输出,对训练集中的预测值 y^(i) y ^ ( i )
误差平方:
一般经验来说,使用平方错误(squared error)来衡量 Loss Function:
L(y^,y)=12(y^−y)2 L ( y ^ , y ) = 1 2 ( y ^ − y ) 2 注意: 但是,对于 logistic regression 来说,一般不适用平方错误来作为 Loss Function,这是因为上面的平方错误损失函数一般是非凸函数(non-convex),其在使用梯度下降算法的时候,容易得到多个局部最优解,而不是全局最优解。因此要选择凸函数。
logistic 回归的损失函数 (Loss Function):
Loss=−(y∗log(y^)+(1−y)log(1−y^)) L o s s = − ( y ∗ l o g ( y ^ ) + ( 1 − y ) l o g ( 1 − y ^ ) )
当 y=1 y = 1 时, L(y^,y)=−logy^ L ( y ^ , y ) = − log y ^ 。如果 y^ y ^ 越接近 1, L(y^,y)≈0 L ( y ^ , y ) ≈ 0 ,表示预测效果越好;如果 y^ y ^ 越接近 0, L(y^,y)≈+∞ L ( y ^ , y ) ≈ + ∞ ,表示预测效果越差;
当 y=0 y = 0 时, L(y^,y)=−log(1−y^) L ( y ^ , y ) = − log ( 1 − y ^ ) 。如果 y^ y ^ 越接近0, L(y^,y)≈0 L ( y ^ , y ) ≈ 0 ,表示预测效果越好;如果 y^ y ^ 越接近1, L(y^,y)≈+∞ L ( y ^ , y ) ≈ + ∞ ,表示预测效果越差;
我们的目标是最小化样本点的损失 Loss Function,损失函数是针对单个样本点的。
补充 log 函数图:
损失函数是,在单个训练样本中定义的,它衡量了在单个训练样本上的表现。
成本函数, 它衡量的是在全体训练样本上的表现。
全部训练数据集的 Loss function 总和的平均值即为训练集的代价函数(Cost function)。
J(w,b)=1m∑i=1mL(y^(i),y(i))=−1m∑i=1m[y(i)logy^(i)+(1−y(i))log(1−y^(i))] J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) log y ^ ( i ) + ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ]- Cost function 是待求系数 w 和 b的函数;
- 我们的目标就是迭代计算出最佳的 w 和 b 的值,最小化 Cost function,让其尽可能地接近于0。
2.4 梯度下降法 (Gradient Descent )
回顾:
1. Loss function (损失函数):是衡量单一训练样本的效果。
2. Cost function (成本函数):成本函数是在全部训练集上,来衡量参数 w 和 b 的效果。
如何使用梯度下降法来训练或学习训练集上的参数 w 和 b
1.Logistic 回归:
y^=σ(wTx+b) y ^ = σ ( w T x + b ) , σ(z)=11+e−z σ ( z ) = 1 1 + e − z , z=wTx+b z = w T x + b 2.Cost function (成本函数):
J(w,b)=1m∑mi=1L(y^(i),y(i))=−1m∑mi=1[y(i)logy^(i)+(1−y(i))log(1−y^(i))] J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) log y ^ ( i ) + ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ] 目的:找到(学习训练得到)w and b ,使得成本函数 J(w,b) J ( w , b ) 最小。
凸函数:全局最优解。(这是我们想要的)
非凸函数:局部最优解。w:=w−α∂J(w,b)∂w w := w − α ∂ J ( w , b ) ∂ w 学习率 learning_rate : α α
我们用 dw,作为导数的变量名,现在我们确保梯度下降法更新是有用的。w 在这对应的成本函数 J(w) 在曲线上的这一点。记住导数的定义,是函数在这个点的斜率,而函数的斜率是高除以宽。
无论你初始化的位置是在左边还是右边,梯度下降法会朝着全局最小值方向移动
梯度下降法
用梯度下降法(Gradient Descent)算法来最小化 Cost function,以计算出合适的 w 和 b 的值。
迭代更新的修正表达式:
b:=b−α∂J(w,b)∂b b := b − α ∂ J ( w , b ) ∂ b 在程序代码中,我们通常使用 dw d w 来表示 ∂J(w,b)∂w ∂ J ( w , b ) ∂ w ,用 db d b 来表示 ∂J(w,b)∂b ∂ J ( w , b ) ∂ b 。
偏导数符号 使用 ∂ ∂ 还是小写字母 d d :取决于你的函数 J 是否含有两个以上的变量 :
1. 变量超过两个就用偏导数符号 ,
2. 如果函数只有一个变量就用小写字母 d。
2.5 导数(Derivatives)
导数,函数的斜率,斜率定义, 高除以宽。
【wiki | 导数】:https://zh.wikipedia.org/wiki/%E5%AF%BC%E6%95%B0
2.6 更多导数的例子 (More derivatives examples)
重点:
- 函数的导数,就是函数的斜率,而函数的斜率在不同的点是不同的。
- 如果你想知道 一个函数的导数,你可参考微积分课本或者维基百科,然后你应该就能,找到这些函数的导数公式。
2.7 计算图 (Computation Graph)
一个神经网络的计算,都是按照前向或反向传播过程来实现的。
2.8 计算图的导数计算 (Derivatives with a Computation Graph )
2.9 logistic 回归中的梯度下降法 (Logistic Regression Gradient Descent)
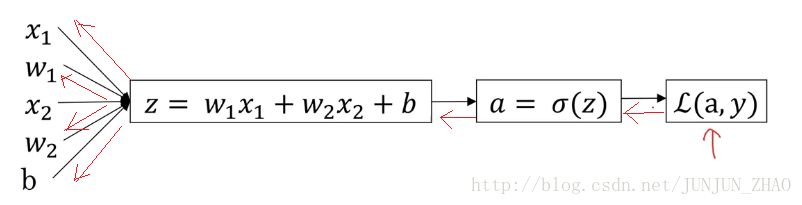
对单个样本而言,逻辑回归 Loss function 表达式:
z=wTx+by^=a=σ(z)L(a,y)=−(ylog(a)+(1−y)log(1−a)) z = w T x + b y ^ = a = σ ( z ) L ( a , y ) = − ( y log ( a ) + ( 1 − y ) log ( 1 − a ) ) 反向传播过程:(红色部分)
前面过程的 da d a 、 dz d z 求导:
da=∂L∂a=−ya+1−y1−adz=∂L∂z=∂L∂a⋅∂a∂z=(−ya+1−y1−a)⋅a(1−a)=a−y d a = ∂ L ∂ a = − y a + 1 − y 1 − a d z = ∂ L ∂ z = ∂ L ∂ a ⋅ ∂ a ∂ z = ( − y a + 1 − y 1 − a ) ⋅ a ( 1 − a ) = a − y 再对 w1、w2和b w 1 、 w 2 和 b 进行求导:
dw1=∂L∂w1=∂L∂z⋅∂z∂w1=x1⋅dz=x1(a−y) d w 1 = ∂ L ∂ w 1 = ∂ L ∂ z ⋅ ∂ z ∂ w 1 = x 1 ⋅ d z = x 1 ( a − y ) 梯度下降法:
w1:=w1−αdw1 w 1 := w 1 − α d w 1 w2:=w2−αdw2 w 2 := w 2 − α d w 2 b:=b−αdb b := b − α d b
2.10 m 个样本的梯度下降 (Gradient Descent on m examples)
m 个样本的梯度下降
对 m 个样本来说,其 Cost function 表达式如下:
z(i)=wTx(i)+by^(i)=a(i)=σ(z(i))J(w,b)=1m∑mi=1L(y^(i),y(i))=−1m∑mi=1[y(i)logy^(i)+(1−y(i))log(1−y^(i))] z ( i ) = w T x ( i ) + b y ^ ( i ) = a ( i ) = σ ( z ( i ) ) J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) log y ^ ( i ) + ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ] Cost function 关于w和b的偏导数可以写成所有样本点偏导数和的平均形式:
dw1=1m∑mi=1x(i)1(a(i)−y(i)) d w 1 = 1 m ∑ i = 1 m x 1 ( i ) ( a ( i ) − y ( i ) ) db=1m∑mi=1(a(i)−y(i)) d b = 1 m ∑ i = 1 m ( a ( i ) − y ( i ) )
2.11 (向量化) Vectorization
向量化(Vectorization)
在深度学习的算法中,我们通常拥有大量的数据,在程序的编写过程中,应该尽最大可能的少使用 loop 循环语句,利用 python 可以实现矩阵运算,进而来提高程序的运行速度,避免 for 循环的使用。
逻辑回归向量化
- 输入矩阵 X X :
- 权重矩阵 w w :
- 偏置 b b :为一个常数
- 输出矩阵: (1,m) ( 1 , m )
所有 m 个样本的线性输出 Z 可以用矩阵表示:
Z=wTX+b Z = w T X + b
Z = np.dot(w.T,X) + b A = sigmoid(Z)import numpy as np # 2.11 Vectorization| 向量化 --Andrew Ng a = np.array([1,2,3,4,5]) print(a) # [1 2 3 4 5] # [Finished in 0.3s] import time # 随机创建 百万维度的数组 1000000 个数据 a = np.random.rand(1000000) b = np.random.rand(1000000) # 记录当前时间 tic = time.time() # 执行计算代码 2 个数组相乘 c = np.dot(a,b) # 再次记录时间 toc = time.time() # str(1000*(toc-tic)) 计算运行之间 * 1000 毫秒级 print('Vectorization vresion:',str(1000*(toc-tic)),' ms') print(c) # Vectorization vresion: 6.009101867675781 ms # [Finished in 1.1s] c = 0 tic = time.time() for i in range(1000000): c += a[i]*b[i] toc = time.time() print(c) print('For loop :',str(1000*(toc-tic)),' ms') # For loop : 588.9410972595215 ms # c= 249960.353586 # NOTE: It is obvious that the for loop method is too slow
2.12 更多向量化的例子 (More Vectorization examples)
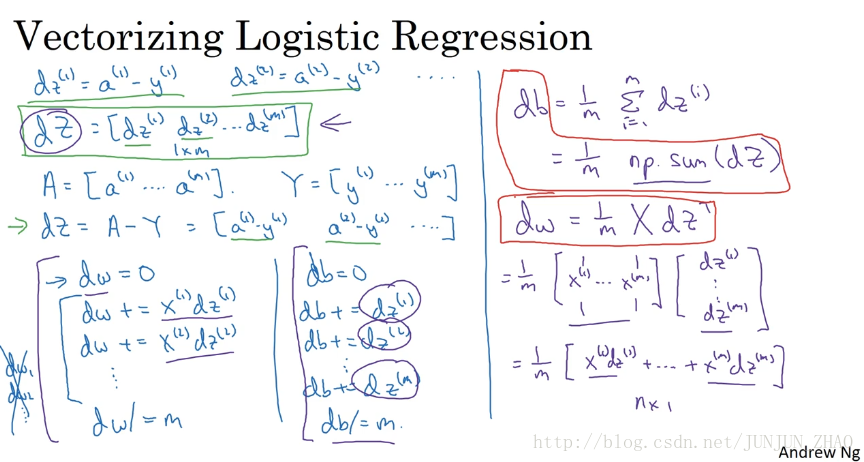
2.13 向量化 Logistic 回归 (Vectorizing Logistic Regression )
2.14 向量化 logistic 回归的梯度输出
Vectorizing Logistic Regression’s Gradient Computation
所有 m 个样本的线性输出 Z Z 可以用矩阵表示:
Z = np.dot(w.T,X) + b A = sigmoid(Z)逻辑回归梯度下降输出向量化
dZ d Z 对于 m m 个样本,维度为,表示为:
dZ=A−Y d Z = A − Y db可以表示为:
db=1m∑mi=1dz(i) d b = 1 m ∑ i = 1 m d z ( i ) db = 1/m * np.sum(dZ)- dw可表示为:
dw=1mX⋅dZT d w = 1 m X ⋅ d Z T dw = 1/m*np.dot(X,dZ.T)单次迭代梯度下降算法流程:
Z = np.dot(w.T,X) + b A = sigmoid(Z) dZ = A-Y dw = 1/m*np.dot(X,dZ.T) db = 1/m*np.sum(dZ) w = w - alpha*dw b = b - alpha*db
2.15 Python 中的广播(Boadcasting in Python )
import numpy as np # 2.15 Boradcasting in python A = np.mat([[56.0, 0.0, 4.4, 68.0], [1.2, 104.0, 52.0, 8.0], [1.8, 135.0, 99.0, 0.9]]) print(A)# axis=0 代表竖直方向(的数据)相加,最后列数不变,行数变化 cal = A.sum(axis=0) print(cal) # [[ 59. 239. 155.4 76.9]] # print("cal.reshape(1,4)",cal.reshape(1,4)) # A/cal 相当于(换算百分比) 100* (56/59) = 94.915 # A 矩阵中的每一个元素,与当前所在列的总和相除 # cal 根据上面的计算本身就是 1 *4 矩阵,所以cal.reshape(1,4) 这个可以不用 percentage = 100 * A / (cal.reshape(1, 4)) print('percentage=', percentage) # [[ 94.91525424 0. 2.83140283 88.42652796] # [ 2.03389831 43.51464435 33.46203346 10.40312094] # [ 3.05084746 56.48535565 63.70656371 1.17035111]]
2.16 关于 python _ numpy 向量的说明(A note on Python_numpy vectors)
# 2.16 A note on python/numpy vectors # 产生随机 5 个高斯变量存储在 a 中 # 官方文档中给出的用法是:numpy.random.rand(d0,d1,…dn) # 以给定的形状创建一个数组,数组元素来符合标准正态分布N(0,1) # 若要获得一般正态分布N(μ,σ^2) 描述则可用sigma * np.random.randn(…) + mu进行表示 a = np.random.randn(5) print('a=', a) # [-0.23427061 -0.79637413 -0.06117785 0.15440186 -1.43061057] # a 的大小 print(a.shape) # (5,) # a 的转置 , print(a.T) # [-0.5694968 -0.23773807 -0.08906264 0.87211753 -0.08380342] # a 和 a 转置的内积 print(np.dot(a, a.T)) # 1.15639015502 # 因为 a.shape (5,) 不规范 # tips tricks 技巧,若要生成随机数组 给出指定的 行列向量 b = np.random.randn(5, 1) print(b) # 这是标准的 5 * 1 的列向量 # [[ 0.10087547] # [-1.2177768 ] # [ 1.55482844] # [ 1.39440708] # [-1.72344715]] print(b.T) # 这是标准的 1 * 5 的行向量 # [[ 0.10087547 -1.2177768 1.55482844 1.39440708 -1.72344715]] # 5 *1 乘以 1 *5 得到的是一个矩阵 5*5 print(np.dot(b, b.T)) # [[ 0.08517485 0.38272589 -0.11342526 0.23506654 0.16852131] # [ 0.38272589 1.71974596 -0.5096667 1.05625134 0.75723604] # [-0.11342526 -0.5096667 0.15104565 -0.31303236 -0.2244157 ] # [ 0.23506654 1.05625134 -0.31303236 0.64873937 0.46508706] # [ 0.16852131 0.75723604 -0.2244157 0.46508706 0.33342507]] # >>> a = np.mat([[1],[2],[3],[4],[5]]) # >>> b = np.mat([[2,2,2,2,2]]) # >>> c = np.dot(a,b) # >>> c # matrix([[ 2, 2, 2, 2, 2], # [ 4, 4, 4, 4, 4], # [ 6, 6, 6, 6, 6], # [ 8, 8, 8, 8, 8], # [10, 10, 10, 10, 10]])虽然在 Python 有广播的机制,但是在 Python 程序中,为了保证矩阵运算的正确性,可以使用
reshape()函数来对矩阵设定所需要进行计算的维度,这是个好的习惯;如果用下列语句来定义一个向量,则这条语句生成的 a 的维度为
(5,),既不是行向量也不是列向量,称为秩(rank)为 1 的 array,如果对 a 进行转置,则会得到 a 本身,这在计算中会给我们带来一些问题。
a = np.random.randn(5)- 如果需要定义
(5,1)或者(1,5)向量,要使用下面标准的语句:
a = np.random.randn(5,1) b = np.random.randn(1,5)- 可以使用
assert语句对向量或数组的维度进行判断。assert会对内嵌语句进行判断,即判断 a 的维度是不是(5,1),如果不是,则程序在此处停止。使用assert语句也是一种很好的习惯,能够帮助我们及时检查、发现语句是否正确。
assert(a.shape == (5,1))- 可以使用
reshape函数对数组设定所需的维度
a.reshape((5,1))
2.17 Jupyter _ ipython 笔记本的快速指南 (Quick tour of Jupyter/ipython notebooks)
Windows jupyter install (Python) 本地搭建
pip3 install jupyter启动 jupyter notebook 命令 cmd
jupyter notebookmac 启动
jupyter-notebook
2.18 logistic 损失函数的解释 (Explanation of logistic Regression cost function)
logistic l o g i s t i c regression 代价函数的解释:
Cost function的由来:
预测输出y^的表达式:
y^=σ(wTx+b) y ^ = σ ( w T x + b )
其中,
σ(z)=11+e−z σ ( z ) = 1 1 + e − z
y^ y ^ 可以看作预测输出为正类(+1)的概率:
y^=P(y=1|x) y ^ = P ( y = 1 | x )
当 y=1 y = 1 时, P(y|x)=y^ P ( y | x ) = y ^ ;
当 y=0 y = 0 时, P(y|x)=1−y^ P ( y | x ) = 1 − y ^ 。将两种情况整合到一个式子中,可得:
P(y|x)=y^y(1−y^)(1−y) P ( y | x ) = y ^ y ( 1 − y ^ ) ( 1 − y )
对上式进行 log l o g 处理(这里是因为 log l o g 函数是单调函数,不会改变原函数的单调性):
logP(y|x)=log[y^y(1−y^)(1−y)]=ylogy^+(1−y)log(1−y^) log P ( y | x ) = log [ y ^ y ( 1 − y ^ ) ( 1 − y ) ] = y log y ^ + ( 1 − y ) log ( 1 − y ^ )
概率 P(y|x) P ( y | x ) 越大越好,即判断正确的概率越大越好。这里对上式加上负号,则转化成了单个样本的 Loss function,我们期望其值越小越好:
L(y^,y)=−(ylogy^+(1−y)log(1−y^)) L ( y ^ , y ) = − ( y log y ^ + ( 1 − y ) log ( 1 − y ^ ) )
对于 m 个训练样本来说,假设样本之间是独立同分布的,我们总是希望训练样本判断正确的概率越大越好,则有:
max∏i=1mP(y(i)|x(i)) max ∏ i = 1 m P ( y ( i ) | x ( i ) )
同样引入 log 函数,加负号,则可以得到 Cost function:
J(w,b)=1m∑mi=1L(y^(i),y(i))=−1m∑mi=1[y(i)logy^(i)+(1−y(i))log(1−y^(i))] J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) log y ^ ( i ) + ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ]
参考文献:
[1]. 大树先生.吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记(1-2)– 神经网络基础
PS: 欢迎扫码关注公众号:「SelfImprovementLab」!专注「深度学习」,「机器学习」,「人工智能」。以及 「早起」,「阅读」,「运动」,「英语 」「其他」不定期建群 打卡互助活动。












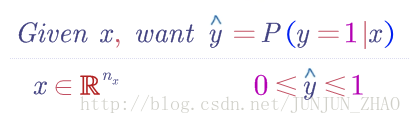





















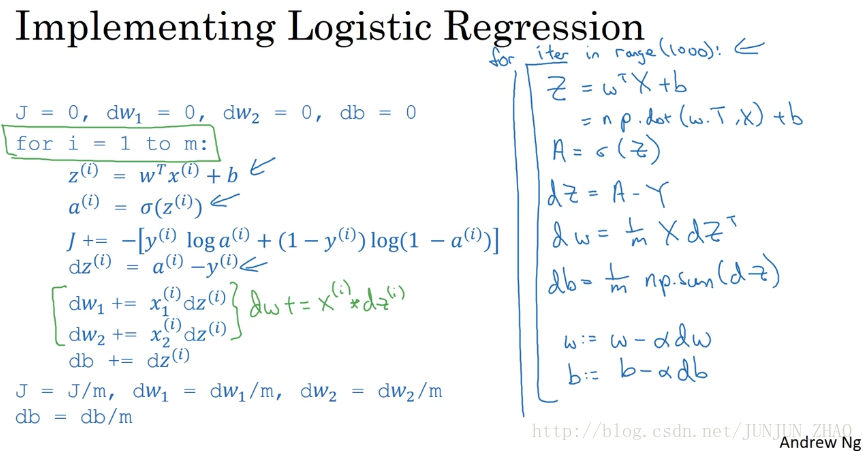

















 116
116

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








