算法提高 最长公共子序列 （DP VS 递归）

算法提高 最长公共子序列  

时间限制：1.0s   内存限制：256.0MB

    

问题描述

　　给定两个字符串，寻找这两个字串之间的最长公共子序列。

输入格式

　　输入两行，分别包含一个字符串，仅含有小写字母。

输出格式

　　最长公共子序列的长度。

样例输入

abcdgh
aedfhb

样例输出

3

样例说明

　　最长公共子序列为a，d，h。

数据规模和约定

　　字串长度1~1000。 

分析：最长公共子序列（LCS）问题是比较经典的DP问题，在《算法导论》15.4小节（P222）有详细的讲解。

这里总结下公式：

此公式图片来自柳婼学姐博客http://blog.csdn.net/liuchuo/article/details/51989144

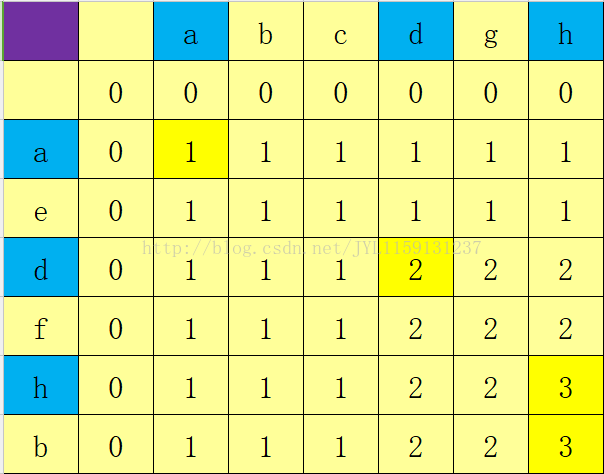
这里对题目给的样例输入按照公式进行填表。

表中的重要部分都进行了高亮标记，最后一个格子即为所求，特别易懂。

#include <iostream>  
#include <string>  
using namespace std;  
int dp[101][101]={{0}};   
int main()  
{  
    string s1,s2;  
    cin>>s1>>s2;  
    for(int i=1;i<=s1.length();i++)//注意从1开始  
        for(int j=1;j<=s2.length();j++)  
        {  
            if(s1[i-1]==s2[j-1])  
                dp[i][j]=dp[i-1][j-1]+1;  
            else  
                dp[i][j]=max(dp[i-1][j],dp[i][j-1]);  
        }  
    cout<<dp[s1.length()][s2.length()]<<endl;  
    return 0;  
}

这道题同样可以使用递归进行求解。

#include<iostream>
#include<string>
using namespace std;
string s1,s2;
int LCS(int i,int j)
{
    if(i>=s1.length()||j>=s2.length())
        return 0;
    else if(s1[i]==s2[j])
        return LCS(i+1,j+1)+1;
    else
        return max(LCS(i+1,j),LCS(i,j+1));
}
int main()
{
    cin>>s1>>s2;
    cout<<LCS(0,0)<<endl;
    return 0;
}

运行结果：