求树中节点的最大距离。
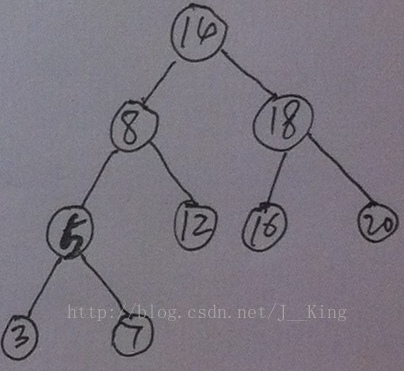
如上图所示,我们要求的距离是3/7到20之间的距离,为5。
我们需要从叶子节点开始计算,对于每一个父节点都要计算通过此节点的两个子节点的最大距离。我们用上溯的方法,具体过程如下:
3、7:depth(深度)为0,maxDis(最大距离)为0
5:depth(深度)为1,maxDis(最大距离)为2
12:depth(深度)为0,maxDis(最大距离)为0:
8:depth(深度)为1+1=2,maxDis(最大距离)为1+2=3
16、20:depth(深度)为0,maxDis(最大距离)为0
18:depth(深度)为1,maxDis(最大距离)为2
14:depth(深度)为2+1=3,maxDis(最大距离)为3+2=5
上面是第一种情况,还有第二种情况是最大距离不通过跟节点,在左子树或者。
还有一个关键的地方是距离的变更,如果最大距离不通过根节点,那么跟节点左右子树最大深度之后还没有其一个子树的最大距离大。
我们用递归的方法来求。由于上溯深度要加1,而最大距离则分为三中情况,1是没有子节点;2是仅有一个子节点;3是有两个子节点。对于大多数有两个子节点的情况,要在原来左右子树最大深度之和上加2(因为加上了两条边),而对于情况1,则加0;对于情况2,则加1。为统一计算,我们假设对于一个NULL的节点(如:叶节点的子节点),深度为
-1,最大距离为0。那么其父节点的深度为-1+1=0;而对于最大距离,一种是左右子树最大深度之和加2,即-1+-1+2=0,另一种便是其左右子树中得最大距离。所以在求最大距离时,我们需要比较着两种情况。所求经过某节点的最大距离是:
最大距离=max(max(左子树最大距离, 右子树最大距离), 左子树最大深度+左子树最大深度+2)。
上程序:
struct Node
{
Node *lChild;
Node *rChild;
};
struct Result
{
int maxDis;
int maxDepth;
};
Result getMaxDis(Tree * T)
{
TreeNode * pNode = T;
if(T == NULL)
{
Result empty = {0, -1};
}
Result lhs = getMaxDis(pNode->lChild);
Result rhs = getMaxDis(pNode->rChild);
Result result;
result.maxDepth = std::max(lhs.maxDepth, rhs.maxDepth)+1;
result.maxDis = std::max(std::max(lhs.maxDis, rhs.maxDis), lhs.maxDepth+rhs.maxDepth+2);
return result;
}






















 327
327

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








