同态滤波(Homomorphic filtering)

1、引言
在生活中会得到这样的图像，它的动态范围很大(即：黑的部分很黑，白的部分很白)，而感兴趣的部分的灰度又很暗(即灰度级范围很小)，分不清物体的灰度层次和细节。采用一般的灰度级线性变换法是不行的，因为扩展灰度级虽然可以提高图像的反差，但会使得动态范围变的更大。而压缩灰度等级，虽然可以减少动态范围，但物体灰度层次和细节就更无法分辨了。同态滤波正好负责解决这种光照分布不均情况下的图像增强问题。
图像的同态滤波(Homomorphic filtering)是把频率过滤和灰度变换结合起来的一种图像处理方法，其是以图像的照度/ 反射率模型作为频域处理的基础，通过调整图像灰度范围和增强对比度来改善图像的质量。使用这种方法可以使图像处理符合人眼对于亮度响应的非线性特性，避免了直接对图像进行傅立叶变换处理的失真。该方法消除图像上照明不均的问题，增强暗区的图像细节，同时又不损失亮区的图像细节。
2、基本原理
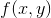
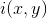
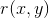
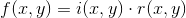
对于一副图像可以由其照度(illumination)函数和反射(reflectance)函数的乘积表示：

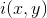
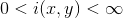
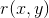
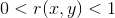
其中，描述景物的照明，与景物无关，；包含景物的细节，与照明无关，。
由于照度相对变化很小，可以看作是图像的低频成份，而反射率则是高频成份。通过分别处理照度和反射率对像元灰度值的影响，达到揭示阴影区细节特征的目的。
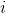
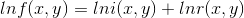
上式中与二者相乘，无法直接用于对照度和反射的频率分量进行操作，因此上式取对数，使在空间域变成相加关系。

对上式两边取傅里叶变换，

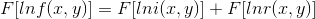
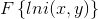
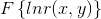
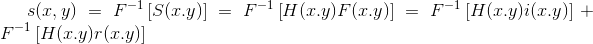
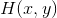
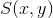
图像的照射分量在空间上变化缓慢，其频谱特性集中在低频段；而反射函数的频谱集中在高频段（景物本身具有较多的细节和边缘），反射函数描述的景物，反映图像的细节内容，特别是在不同物体的连接部分。，其频率处于高频区域。这些特性导致图像取对数后的傅里叶变换的低频成分与照射相联系，而高频成分与反射相联系。
（同态滤波函数，可分别作用在照度分量上和反射分量上），式中，是傅里叶变换的结果，在空间域中。
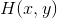
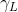
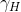
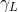
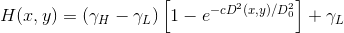
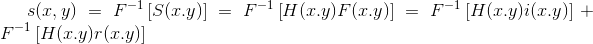
使用同态滤波器可以更好地控制照射分量和反射分量。这种控制器需要指定一个滤波器函数，它可用不同的可控方法影响傅里叶变换的低频和高频。如果和选定，而<1且>1，那么滤波器函数趋近于衰减低频（照射）的贡献，而增强高频反射的贡献。最终结果是同时进行动态范围的压缩和对比度的增强。



令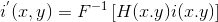

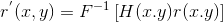
则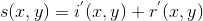
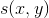
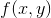
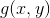
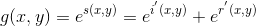
最后，由于是原始图像取对数得到的，相反的操作就能产生符合要求的增强图像，由表示，也就是：

算法流程

其中表示原始图像；代表对数运算；DFT 代表傅立叶变换（实际操作中运用快速傅立叶变换FFT）；IDFT 代表傅立叶逆变换（实际操作中运用快速傅立叶逆变换IFFT）；exp 代表指数运算。
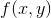
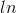
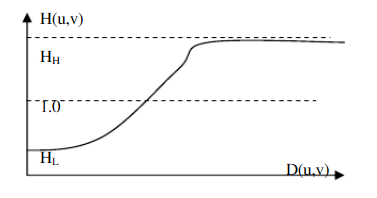
3、同态滤波器的设计
假如图像照明不均，则图像上各部分的平均亮度会有起伏。对应于暗区的图像细节结构就较难分辨，需要消除这种不均匀性。可以压缩照明函数的灰度范围，也就是在频域上削弱照明函数的成分，同时增强反射函数的频谱成分，就可以增加反映图像对比度的反射函数的对比度。结果，使图像上暗区图像细节得以增大，并尽可能大的保持亮区的图像细节。由乘上传递函数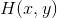——(同态滤波器)，低频段被压缩，而高频段却扩展了。
高斯型高通滤波修改形式：

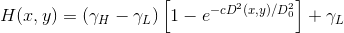
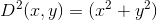
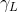
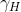
式中， 常数c用于控制坡度的锐利度，它在和之间过渡。
根据不同的图像特性和需要，选用不同的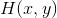，可得到满意的结果。这个滤波器类似于高斯高频强调滤波器。
4、实验结果

作者：Jacky_Ponder，转载或分享请注明出处。QQ:2814152689