牛客2022 暑期多校6 B Eezie and Pie（树上差分 + 倍增求第 kth 祖先板子）

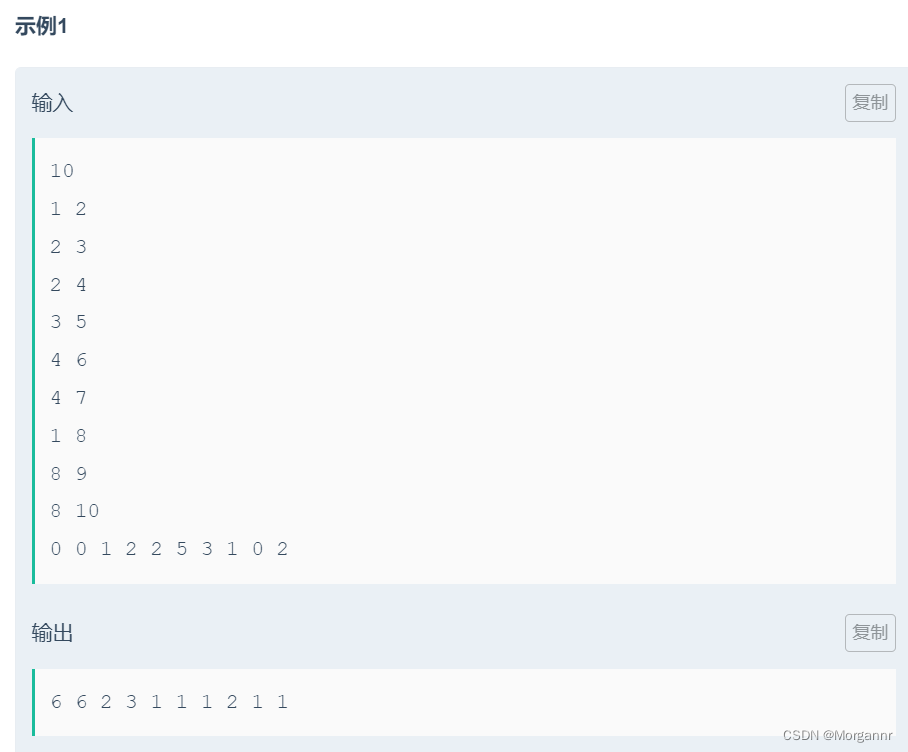
题意：

给定一棵树，要求输出 以 u 为 根的子树中，有多少个节点权值满足 大于等于 其到 根节点 u 的 距离，u ∈ 1 ~ n。

思路：

以一棵 根节点为 u 的子树 为例子，我们从 贡献 的角度来分析问题。

对于 子树中的某个节点（任意节点，包括 根），我们分析一下 它对根节点造成的贡献。（贡献 指的是 满足条件的节点个数）

• 首先，任意节点都会 使它自己的贡献加 1。
• 其次，假设 节点权值为 w[u]，它会使得 其朝向根节点的路径 u ~ v（路径长度为 w[u]）上 所有节点 的贡献都 加上一个 1。

举个例子，以题中的样例为例子：节点 6 的权值为 3，那么它会使得 6 -> 4 -> 2 -> 1 这条路径上所有点贡献加 1。

首先我想的是 树链剖分，因为 树链剖分 可以 使树上的某一条路径转化为 logn 段连续区间，进而用 线段树 进行 区间修改操作，但是由于其 时间复杂度是 O(n(logn)^2) 级别，题设 范围是 2e6，显然是不被允许的。

那还有什么算法可以 对树上某条路径进行修改 呢，我们可以想到一个更优雅的做法，树上差分。

之前有提到过 一维数组的差分，可以 用 O(1) 的时间复杂度完成对一段区间加上某个数的操作，树上差分 也是类似。

具体做法：

• 树上差分标记，我们 在 dfs 的过程中完成。
• 当向下 搜索到某个节点 u 时，我们 令 k 等于 其权值 w[u]，前文已经提及，我们 目的是要将 u ~ v 这条长度为 k 的路径整体 + 1，那么转化为 差分操作，就是 在 u 节点 mark[u] ++，在 v 的父节点 mark[fa[v][0]] --（其中，v 为 u 的 第 k 个祖先：v = get_fa(u, w[u])），即可完成。
  （此处类比 一维数组差分 帮助理解：在 区间 i ~ j 上加上 a，就应当 使差分数组 c[i] += a，c[j + 1] -= a ）

void dfs(int u, int father) {
    int v = get_fa(u, w[u]);
    mark[u]++, mark[fa[v][0]]--;

    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        dfs(j, u);
    }
}

• 如何求 u 的 第 k 个祖先 v ，如果暴力的话，显然是会 超时 的，要 倍增 地找（下面这个板子很重要，用于 倍增地查找 节点 x 的 第 kth 祖先）。

int get_fa(int x, int k) {
	for (int i = 21; i >= 0; --i)
	{
	    if (k >= (1 << i))	//如果 k 满足这个条件就一直跳，直到跳到目的地为止
	    {
	        k -= (1 << i);
	        x = fa[x][i];
	    }
	}
	return x;
}

• 之后进行 第二遍 dfs1，用于 自下而上合并所有节点的差分数组 mark[u]，类比 将一维差分数组 for 一遍 前缀和 求 原数组。至此，我们就完成了 对树上路径的修改操作。

void dfs1(int u, int father) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        dfs1(j, u);
        mark[u] += mark[j];
    }
}

时间复杂度：

$O(nlogn)$

代码：

#include <bits/stdc++.h>

using namespace std;
//#define map unordered_map
#define int long long
const int N = 2e6 + 10, M = N << 1;
int n;
int h[N], e[M], ne[M], w[N], idx;
int fa[N][22];
int depth[N];
int mark[N];

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs(int root)
{
    queue<int> q; q.push(root);
    while (q.size())
    {
        auto t = q.front(); q.pop();
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (depth[j] > depth[t] + 1)
            {
                depth[j] = depth[t] + 1;
                fa[j][0] = t;
                for (int k = 1; k <= 21; ++k)
                {
                    fa[j][k] = fa[fa[j][k - 1]][k - 1];
                }
                q.push(j);
            }
        }
    }
}

void init(int root)	//经典的对 fa 数组预处理的操作
{
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[root] = 1;
    bfs(root);
}

int get_fa(int x, int k) {
    for (int i = 21; i >= 0; --i)
    {
        if (k >= (1 << i))
        {
            k -= (1 << i);
            x = fa[x][i];
        }
    }
    return x;
}

void dfs(int u, int father) {
    int v = get_fa(u, w[u]);
    mark[u]++, mark[fa[v][0]]--;

    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        dfs(j, u);
    }
}

void dfs1(int u, int father) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        dfs1(j, u);
        mark[u] += mark[j];
    }
}

signed main()
{
    memset(h, -1, sizeof h);
    cin >> n;
    int t = n - 1;
    while (t--)
    {
        int u, v; scanf("%lld%lld", &u, &v);
        add(u, v), add(v, u);
    }
    for (int i = 1; i <= n; ++i) {
        scanf("%lld", &w[i]);
    }
    init(1);
    dfs(1, -1);
    dfs1(1, -1);
    for (int i = 1; i <= n; ++i) {
        printf("%lld ", mark[i]);
    }

    return 0;
}