DAY17.
第一类曲面积分
对面积的曲面积分
形式: ∬ ∑ f ( x , y , z ) d s \iint_{\sum} f(x,y,z) d_s ∬∑f(x,y,z)ds
例题
求 ∬ ∑ d s \iint_{\sum} d_s ∬∑ds 其中 ∑ = 2 − ( x 2 + y 2 ) \sum = 2 - (x^2+y^2) ∑=2−(x2+y2)在 xoy 平面上的部分
解:
∑ \sum ∑的区域画图为:

总体为一个圆锥体,其中投影面为S { z = 0 x 2 + y 2 ⩽ 2 \begin{cases} z = 0 \\ x^2+y^2 \leqslant 2\end{cases} {z=0x2+y2⩽2
∬ ∑ d s \iint_{\sum} d_s ∬∑ds
= ∬ D x o y 1 + 4 x 2 + 4 y 2 d x d y = \iint_{D_{xoy}} \sqrt{1+4x^2+4y^2}d_xd_y =∬Dxoy1+4x2+4y2dxdy
= ∫ 0 2 π d θ ∫ 0 2 1 + 4 ρ 2 ρ d ρ = \int_0^{2\pi} d_{\theta} \int_0^{\sqrt 2 } \sqrt{1+4 \rho^{2}}\rho d_{\rho} =∫02πdθ∫021+4ρ2ρdρ
= 2 π ∗ 1 8 ∫ 0 2 1 + 4 ρ 2 d 1 + 4 ρ 2 =2 \pi * \frac{1}{8} \int_0^{\sqrt 2} \sqrt{1+4 \rho^2}d_{1+4\rho^2} =2π∗81∫021+4ρ2d1+4ρ2
= 13 3 π = \frac{13}{3}\pi =313π
第二类曲面积分
对坐标的曲面积分
此时的积分形式为: I = ∬ ∑ P ( x , y , z ) d y d z + Q ( x , y , z ) d x d z + R ( x , y , z ) d x d y I = \iint_{\sum} P(x,y,z)d_yd_z+Q(x,y,z)d_xd_z+R(x,y,z)d_xd_y I=∬∑P(x,y,z)dydz+Q(x,y,z)dxdz+R(x,y,z)dxdy
例题
求 I = ∬ ∑ x 2 y 2 z d x d y I = \iint_{\sum} x^{2} y^2 z d_xd_y I=∬∑x2y2zdxdy,其中 ∑ \sum ∑为 x 2 + y 2 + z 2 = a 2 x^2+y^2+z^2 =a^2 x2+y2+z2=a2的下半部分。
解:画出 ∑ \sum ∑的区域如图
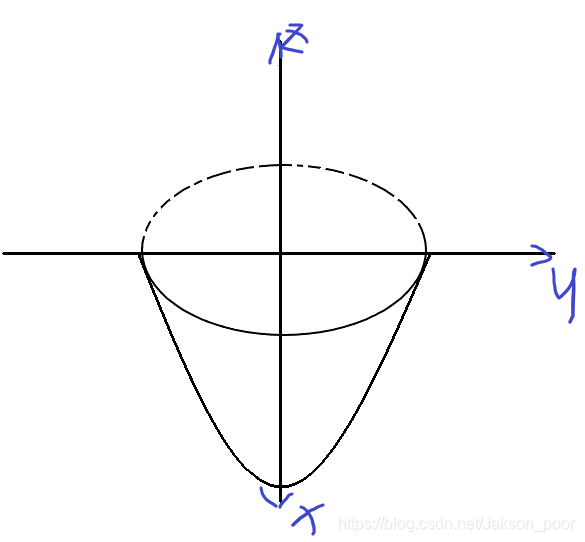
D x o y = { x 2 + y 2 ⩽ a 2 z = 0 D_{xoy} = \begin{cases} x^2+y^2 \leqslant a^2 \\ z = 0 \end{cases} Dxoy={x2+y2⩽a2z=0
I = ∬ ∑ x 2 y 2 z d x d y I = \iint_{\sum} x^{2} y^2 z d_xd_y I=∬∑x2y2zdxdy
= ∬ D x o y x 2 y 2 a 2 − x 2 − y 2 ( − d x d y ) =\iint_{D_{xoy}} x^2y^2 \sqrt{a^2-x^2-y^2}(-d_xd_y) =∬Dxoyx2y2a2−x2−y2(−dxdy)
为什么是 − d x d y -d_xd_y −dxdy呢,因为下部分的法线和z轴的内积为负
= ∬ D x o y ( ρ cos θ ) 2 ( ρ sin θ ) 2 − a 2 − ρ 2 ρ d ρ =\iint_{D_{xoy}} (\rho \cos \theta)^2 (\rho \sin \theta)^2 -\sqrt{a^2 - \rho ^2} \rho d_{\rho} =∬Dxoy(ρcosθ)2(ρsinθ)2−a2−ρ2ρdρ
下面的计算过程略
高斯公式
形式: ∭ Ω P d x d z + Q d y d z + R d x d y = ∭ Ω ( ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z ) \iiint_{\Omega} Pd_xd_z+Qd_yd_z+Rd_xd_y=\iiint_{\Omega}(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}) ∭ΩPdxdz+Qdydz+Rdxdy=∭Ω(∂x∂P+∂y∂Q+∂z∂R)
要使用高斯公式的前提是:
- 整个积分区域封闭
- 外侧的方向为正
- ∂ P ∂ x , ∂ Q ∂ y , ∂ R ∂ z \frac{\partial P}{\partial x},\frac{\partial Q}{\partial y},\frac{\partial R}{\partial z} ∂x∂P,∂y∂Q,∂z∂R存在且连续








 本文详细介绍了第一类和第二类曲面积分的概念及计算方法,并通过具体例题进行了解释。同时,还深入探讨了高斯公式,包括其适用条件和计算步骤,为读者提供了全面的理解。
本文详细介绍了第一类和第二类曲面积分的概念及计算方法,并通过具体例题进行了解释。同时,还深入探讨了高斯公式,包括其适用条件和计算步骤,为读者提供了全面的理解。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








