最详细浅入深出机器学习_单变量线性回归算法

吴恩达机器学习算法（一）

名不显时心不朽

单变量线性回归

单变量线性回归，这种机器学习算法常被用来预测房价，商品的市值等可根据原有的数据推断出最终的实际结果的情况，属于监督学习的一种。

问题开始的描述

假如现在你有一个朋友，想将他的一所闲置房售出，所以来询问你他这所房子大概可以买多少钱。而你现在有一组数据，其中有近来统计的：房子的大小与售出价格的点图

这个问题此时来看，用我们现在所学到的基础数学知识，我们可以理所当然的想到根据这些点来画一条直线，画这条直线的依据是让它尽可能的通过更多已经在图中瞄出来的点。

这种思想当然也在机器学习中出现，它的术语叫做拟合

但是问题是如果我们想要我们得到的结果更加精确呢？

将图中的数据用表表示如下：

我们用 X 表示房子的大小，Y 表示预测的价格

很显然的我们可以有一个一次函数的雏形：

$h_{\theta }(x)={\theta }_{0}x+{\theta }_1$

插入一段监督学习算法的工作方式

在这个问题中，其实更具体的说这是个回归问题。回归一词指的是，我们根据之前的数据预测出一个准确的输出值，对于这个例子就是房子的售出价格。

上图显示出算法工作的流程：我们把已知的房屋价格与大小的关系喂给我们的学习算法，然后输出一个函数 h ，然后我们再将要预测的房子大小 x 输入给 h 最后 h 将预测的 y 输出

这就是算法的工作流程，我希望我表述的很简单，你们都很容易看懂。

损失（代价）函数

在上面的问题描述中，我们假设了一个一次线性函数$h_{\theta }(x)={\theta }_{0}x+{\theta }_1$

但是我们没有解决如何让这个函数最好的拟合我们的数据，已达到相对准确的输出结果

其实现在我们要解决的事情是如何挑选最合适的两个参数：${\theta }_0以及{\theta }_1$

这两个参数最终决定了我们最后得到的直线的准确程度，当然我们开始所预测的指肯定会与我们准确的值有所误差，就像下面这个图一样

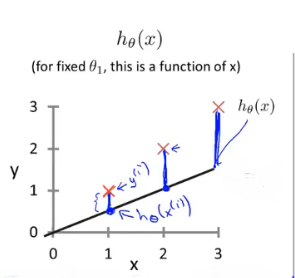
这幅图里面，我们取了${\theta }_0=0.5,{\theta }_1=0$ 我们可以明显的看到，直线与实际数据之间的误差（也就是蓝色的线），我们称为建模误差

现在我们的目标是如何有效的减小建模误差，选择出可以使建模误差平方和最小的模型参数。这样就引出了损失函数：

$J({\theta }_0,{\theta }_1)=\frac{1}{2m}{\Sigma }_{i=1}^m(h_{\theta }(x^i)-y^i{)}^2$

其实我在看到这点的时候很容易的联想到了中学时代的方差公式，其作用就是度量随机变量与数学期望之间的偏离程度

我们将为损失函数做一个等高线图：

其中底面的坐标分别是${\theta }_0,{\theta }_1,竖直坐标为J$

我们可以发现在三维空间里面的确存在一个让 J 损失函数最小的解（图像的底部）

若是不好理解的话，我们可以做出一个损失函数J与 预测函数 h 的平面图像，就像三维空间里面的一样，在平面图形中也的确存在一个点${\theta }_0=1$使 J 最小

注意图中取的是${\theta }_1$这是因为我和它的预测函数 h 形式不一样，我们理解为 ${\theta }_0$

梯度下降

当我们明白了如何构建损失函数J，并且懂了损失函数 J 是为了让预测函数 h 更加拟合我们的数据的时候，我们就已经完成了三分之二了

但是我们需要的算法是一种更加智能的算法，它更加的有效，我们不希望人工的通过不断的读图来改变参数${\theta }_0,{\theta }_1$

我们构造的是一种能够自动地找出这些使损失函数 J 取最小值的${\theta }_0,{\theta }_1$算法

梯度下降算法就是这样一种算法，它可以自动的帮我们找出函数的最优解

其背后的思想是：开始我们随机的选择一个参数的组合$({\theta }_0,{\theta }_1,{\theta }_2...{\theta }_n)$，计算损失函数，然后我们寻找下一个能让损失函数值下降最多的函数组合。持续这么做直到一个局部最小值，因为我们没有尝试完所有的参数组合，所以不能确定我们得到的最优解为局部最优解还是全局最优解，选择不同的初参数组合，可能会得到不同的局部最小值。

这个过程就像上图一样，从红色的顶部一步一步的下降到蓝色的底部。

很形象的比喻就是如何快速的下山，每走一步就旋转360°寻找一次最陡的下降路径，直到到达局部的最低点

注意这里是局部而不是全局，在上图中两个红色箭头的位置就是两个不同的局部最低点。但是只有一个才是全局最低点。

梯度下降算法的式子为：

repeat until convergence {

${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)$ (for j = 0 and j = 1)

}

其中$\alpha$是学习率。它决定我们沿着能让损失函数下降程度最大的方向，向下迈出的步子有多大。在梯度下降中，我们每一次都同时让所有的参数减去学习率乘以损失函数的偏导数。

值得注意的是，在进行梯度下降的过程中，我们需要不断的更新${\theta }_0,{\theta }_1$这两个参数，当j = 0 和 j = 1的时候会产生更新

就像上图一样，当${\theta }_0=temp0,{\theta }_1=temp1$两者都计算完成才会更新整个式子，这称为同步更新，事实上，当谈到梯度下降时很多时候都意味着进行同步更新。

可能到现在你都还没有了解清楚梯度下降到底是如何工作的，下面我们进一步诠释它的内涵

在这个例子中，我们的要求是自动找到损失函数J所能取到的最小值，因此我们引入的梯度下降算法。

事实上，梯度下降就是在帮我们不断的对损失函数J进行求导微分，在上图的第一幅图里，我们开始的参数选择在红点那里，当我们进行一次梯度微分时，我们会得到一个${\theta }_0$（通过对损失函数J的微分），然后梯度算法里面的${\theta }_0={\theta }_0-\alpha {\theta }_0$ 其中$\alpha$学习率为一个正数，这样更新一次后，${\theta }_0$是减小的，因此红点应该往损失函数切线斜率减小的方向移动，也就是往下移动，就这样循环往复最终我们会达到损失函数J的最低点。

当达到损失函数的最低点时，此时我们再对损失函数微分，我们发现${\theta }_0=0$，因此之后在梯度下降算法里面参数 ${\theta }_0={\theta }_0-\alpha {\theta }_0$ 的值不再改变，这就是梯度下降算法的工作原理。

同理当初参数选择为下图那个点的时候，梯度下降算法也可以达到损失函数的最低点。

梯度下降的学习率

我们在上面说过，$\alpha$为梯度下降算法的学习率，它决定我们沿着能让损失函数下降程度最大的方向，向下迈出的步子有多大。对于学习率的取值有大有小，但是我们需要的是一个合适大小的学习率。

在上面这幅图里面，第一幅是学习率太小的情况，我们可以看到，当$\alpha$很小的时候，对于损失函数的迭代次数会很多，这样的话会耗费很长的时候来得到一个最优解。

当$\alpha$很大的时候，我们可以看到在下面这幅图里面，损失函数下降的步子太大，以至于越过了最低点。

使用梯度下降的线性回归

当我们充分了解了上面的几种算法的工作原理，我们就可以将这种算法应用到开场我们提出的问题中。

其关键在于求出损失函数的导数：

计算过程大概就是：

${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)\to {\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}\frac{1}{2m}{\Sigma }_{i=1}^m(h_{\theta }(x^i)-y^i{)}^2$

微分的时候再把预测函数 $h_{\theta }(x)={\theta }_{0}x+{\theta }_1$ 代入计算就好了

最终它应该长这样：

演示过程

左图为预测函数、右图为损失函数（最低点为中间的小圆圈）

初始化：

利用梯度下降迭代：

最后达到最优解

左边的预测函数达到适当拟合状态，右边的损失函数达到最低点。

至此机器学习的第一个基础算法已经完成，希望看到这里的你们能够完全弄懂。