链表的专用题型-链表的经典算法（循环链表的经典应用（约瑟夫问题））

最新推荐文章于 2025-04-19 00:15:51 发布

Jason_from_China

最新推荐文章于 2025-04-19 00:15:51 发布

阅读量942

点赞数 9

分类专栏：数据结构知识点的补充文章标签：链表算法数据结构 c语言开发语言

本文链接：https://blog.csdn.net/Jason_from_China/article/details/137845297

版权

数据结构知识点的补充专栏收录该内容

50 篇文章

订阅专栏

本文介绍了约瑟夫问题的背景和解决方法，重点讨论了如何使用循环链表模拟此问题，包括模拟法、数学法、递归法、迭代法以及动态规划的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

链表的经典算法（循环链表的经典应用（约瑟夫问题））

约瑟夫问题（Josephus Problem）是一个著名的数学问题，起源于古罗马时期。问题描述如下：
有一圈人围坐在一起，每个人都有一个编号。从第一个人开始报数，数到三的人会被杀掉，然后从下一个人重新开始报数，重复这个过程，直到所有人都被杀掉为止。问最后剩下的是谁？
约瑟夫问题的解题思路可以通过不同的数学方法来探讨，以下是几种常见的解题方法：
1. 模拟法：
通过编程或者手动模拟这个过程，不断剔除数到3的人，直到圈中只剩下一人。这种方法直观但效率不高，对于人数较多的情况不适用。
2. 数学法（循环队列）：
如果人数较少，可以通过数学方法直接计算出最后剩下的人的编号。假设总人数为n，当n是3的倍数时，最后剩下的是第n/3个人；当n不是3的倍数时，最后剩下的是第(n+1)/3个人。这是因为每轮结束后，编号为3的倍数的人都会被剔除，所以每轮结束后剩下的人数实际上是原来人数的三分之一。
3. 递归法：
利用递归思想，定义函数f(n)表示n个人围坐一圈时最后剩下的人的编号。根据约瑟夫问题的规则，f(n)可以表示为f(f(n-1)) + 1。通过递归调用这个函数，可以得到最后剩下的人的编号。
4. 迭代法：
类似于递归法，但是使用迭代的方式来实现。可以通过循环来不断计算下一轮剩下的人的编号，直到只剩下一人。
5. 动态规划法：
对于更一般的情况，即约瑟夫问题的变体，可以使用动态规划的方法来解决。例如，如果每次数到m的人会被杀掉，可以使用状态转移方程来计算最后剩下的人的编号。
约瑟夫问题还有许多变体，例如双向约瑟夫问题、约瑟夫问题的高级版本等，解决方法也会因问题的不同而有所差异。

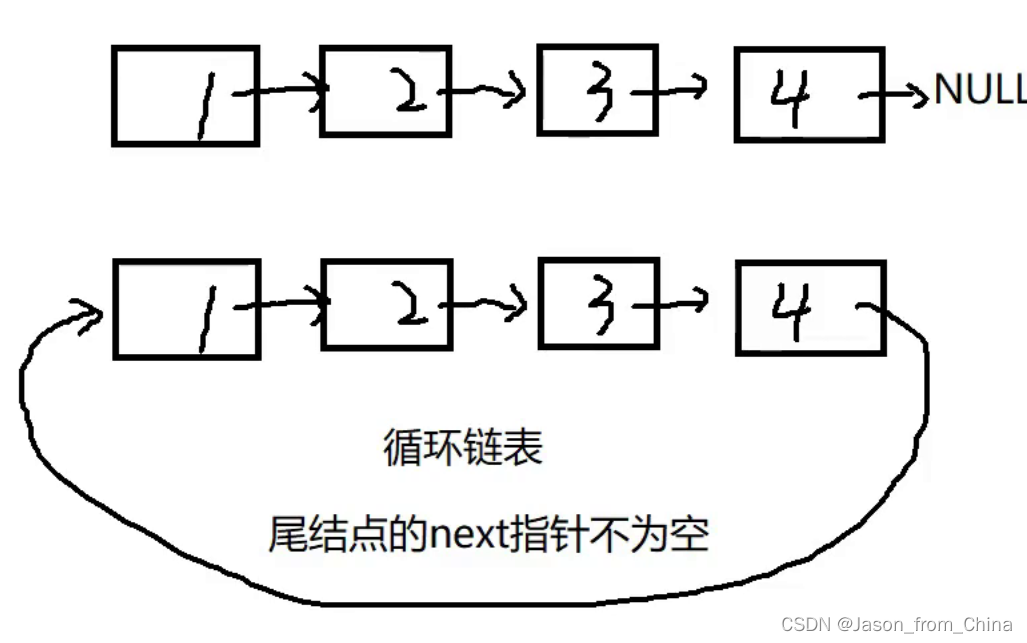
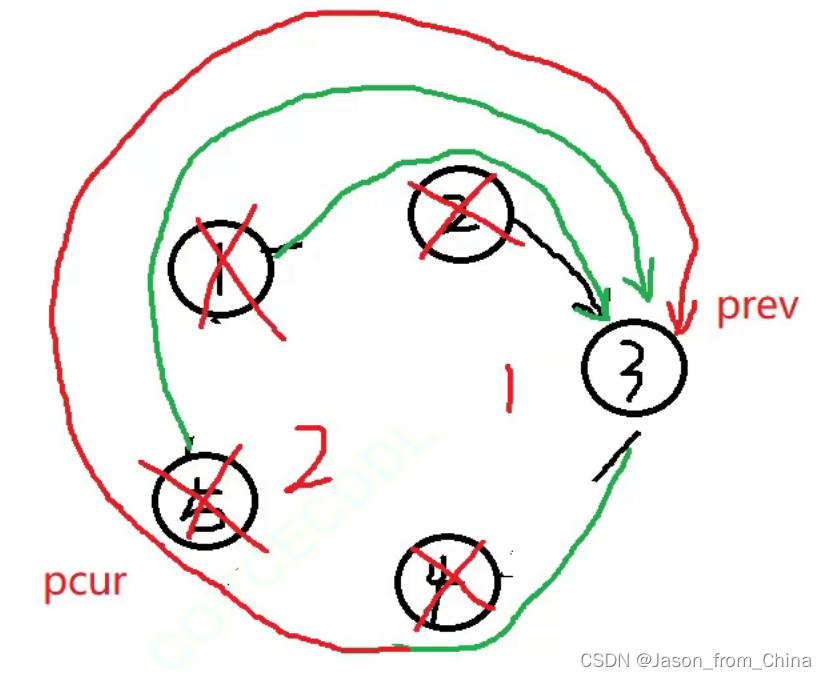
prev先指向pcur的下一个节点

已经成环了，所以只要当前节点下一个节点不是，就可以一直循环，要是下一个节点是第一个节点，说明此时节点只有一个节点，可以返回了

瑟夫问题（Josephus Problem）是一个著名的数学问题，它涉及到在循环链表中删除特定编号的节点。问题的描述是这样的：假设有一圈人围坐在一起，每个人都有一个编号。从第一个人开始报数，数到某个特定数字的人就会被淘汰，然后从下一个人开始重新报数，重复这个过程，直到最后只剩一个人。约瑟夫问题可以通过多种方法解决，其中一种经典的方法是使用循环链表。

以下是使用循环链表解决约瑟夫问题的步骤：

创建一个循环链表，每个人都是一个节点，节点包含一个数据域（编号）和一个指针域（指向下一个节点的指针）。
初始化一个指针，指向链表的头节点。
进行报数操作：
- 从头节点开始，每次移动指针数到指定的数字。
- 当指针指向的节点编号等于指定的数字时，删除该节点（在链表中删除节点需要更新前后节点的指针）。
- 如果链表中只剩下一个节点，则直接返回该节点。
- 如果指针指向的节点是最后一个节点，则需要特殊处理，因为删除节点后需要继续下一次报数。这时，可以将头指针指向链表的第二个节点，然后继续报数。

重复步骤3，直到只剩下一个节点。

#include <stdio.h>
typedef struct ListNode ListNode ;
//创建节点
ListNode* newnode(int x)
{
    //防止开辟空间失败，使用节点进行接收
    ListNode*node=(ListNode*)malloc(sizeof(ListNode));
    if(node==NULL)
    {
        perror("node");
        exit(1);
    }
    //开辟成功以后进行赋值
    ListNode*pure=node;
    pure->val=x;
    pure->next=NULL;
    return pure;
}
//形成环形链表,n需要多大的环形链表
ListNode* circlenode(int n)
{
    //创建第一个节点
    ListNode* headnode=newnode(1);
    //循环节点(运动的节点)开始指向头结点，下一个就是新开辟的节点
    ListNode* patilenode=headnode;
    //循环创建节点
    for (int i=2; i<=n; i++) 
    {
    patilenode->next=newnode(i);
    //链接下一个节点
    patilenode=patilenode->next;
    }
    //形成环形链表
    patilenode->next=headnode;
    return headnode;
}
//实现约瑟夫问题，n是创建的节点的个数，2是第几个死亡
int ysf(int n, int m )
{
    //返回的头节点
    ListNode*head=circlenode(5);
    //运行的节点（循环的节点）
    ListNode*pure=head;
    //需要删除的节点
    ListNode*del=pure;
    //pure找到尾结点
    while (pure->next!=del) 
    {
        pure=pure->next;
    }
    int count=1;
    
    while (pure->next!=pure) 
    {
        if (count==m) 
        {
            //把节点进行改变
            pure->next=del->next;

            //把删除的节点，但是没有进行释放
            //del=del->next;
            
            //删除节点并未进行释放
            free(del);
            del=pure->next;
            //重新赋值,这里赋值的是1，如果是0的情况需要-1==m
            count=1;
        }
        else 
        {
            //循环寻找下一个节点
            del=del->next;
            pure=pure->next;
            //进行计数，这里是判断m用的，m到第几个了
            count++;
        }
        
    }
    return pure->val;
}