图像处理 - GLCM灰度共生矩阵如何计算

因为最近要在OpenCV上试试各种图像分割算法的效果，其中灰度共生算法没有办法直接调用库函数实现，看了很多文章，其中有一篇博文讲的很清楚。博主有提供原理和源码，大家可以直接看原博。

原文地址：纹理特征提取方法：LBP, 灰度共生矩阵

我现在按照自己的理解以代码逻辑再复盘一遍算法过程，详细推导一遍，有一些是上面那个博文搬过来的，本文只是学习笔记，以便日后查询使用。

// 在计算灰度共生矩阵前需要确定一些参数：

1. 灰度共生矩阵灰度级，与灰度共生矩阵的阶数相同，即当灰度图像灰度级为N时，灰度共生矩阵为N × N的矩阵。一般一幅图的灰度级有256级，0-255，但由于计算量大，一般选取4、8、16作为灰度级；
2. 滑动窗口尺寸，即每次计算特征值所选用的窗口矩阵大小，一般选取5x5或7x7；
3. 方向选择：计算灰度共生矩阵的方向一般为0°，45°，90°，135°四个方向；求出四个方向矩阵的特征值后，可以通过计算四个特征值的平均值作为最终特征值共生矩阵；
4. 步距d：一般选择d = 1，即中心像素直接与其相邻像素点做比较运算；
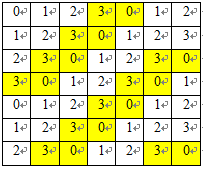
5. 为了解释说明方便，用N=4个灰度级，7*7窗口矩阵作为示例。

// 具体步骤如下：

1. 将原图灰度量化

原图的灰度级为256时，当分成N个灰度级时，直接将像素点的灰度值除以(256/N)取整。比如，选择4灰度级，就将像素点灰度值除以64即可。图a灰度级为4的7*7窗口矩阵。

2. 计算一个矩阵窗口中，按照某个方向统计的灰度共生矩阵

A. d=1,求0°方向矩阵A的共生矩阵

则按照0°方向（即水平方向从左向右，从右向左两个方向）,共有以下几种情况：
1/ 统计矩阵值(0, 1)，则如下图所示：

此时满足矩阵值(0,1)统计条件的值，共有10个，所以该窗口对应的GLCM统计矩阵的(0, 1)和(1, 0)位置元素的值即为10。

2/ 统计矩阵值(1, 2)，则如下图所示：

此时满足矩阵值(1,2)统计条件的值，共有11个，所以该窗口对应的GLCM统计矩阵的(1, 2)和(2, 1)位置元素的值即为11。

3/ 统计矩阵值(2, 3)，则如下图所示：

此时满足矩阵值(2,3)统计条件的值，共有11个，所以该窗口对应的GLCM统计矩阵的(2, 3)和(3, 2)位置元素的值即为11。

4/ 统计矩阵值( 3,0)，则如下图所示：

此时满足矩阵值(3,0)统计条件的值，共有10个，所以该窗口对应的GLCM统计矩阵的(3, 0)和(0, 3)位置元素的值即为10。

最后的GLCM 4 × 4统计矩阵结果如下：

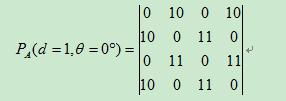
B. d=1,求45°方向矩阵A的共生矩阵

则按照45°方向（即45°方向从右上向左下，从左下向右上两个方向）,共需统计以下4种情况：统计矩阵值(0,0)(1, 1),(2,2)(3,3)。
具体分析如A同理，最后的GLCM 4 × 4统计矩阵结果如下：

C. d=1,求90°方向矩阵A的共生矩阵

计算方法类似上述。

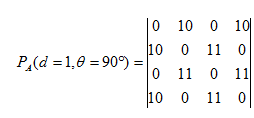
D. d=1,求135°方向矩阵A的共生矩阵

计算方法类似上述。

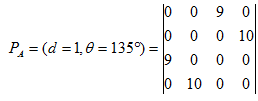
3. 矩阵的归一化

将矩阵所有元素与矩阵中所有元素之和作除运算，得到概率矩阵。

用P表示灰度共生矩阵的归一化频率矩阵，其中i, j表示按照某方向同时出现于两个像素的某两个级别的灰度值，所以P(i, j)表示满足这种情况的两个像素出现的概率。 以上述情景B中的矩阵为例： 原矩阵为：

归一化后，矩阵形式变为：

4. 计算单窗口灰度共生矩阵特征值

我们一般采用四个最常用的特征来提取图像的纹理特征：能量、对比度、相关度、熵。
a. 能量（角二阶距）

能量是灰度共生矩阵各元素的平方和，又被称角二阶距。它是图像纹理灰度变化均一的度量，反映了图像灰度分布均匀程度和纹理粗细程度。

b. 对比度

对比度是灰度共生矩阵主对角线附近的惯性矩，它体现矩阵的值如何分布，反映了图像的清晰度和纹理沟纹的深浅。

c. 相关度

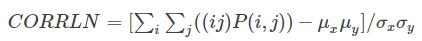
用来度量图像的灰度级在行或列方向上的相似程度，因此值得大小反应了局部灰度相关性，值越大，相关性也越大。

d. 熵

图像包含信息量的随机性度量。当共生矩阵中所有值均相等或者像素值表现出最大的随机性时，熵最大；因此熵值表明了图像灰度分布的复杂程度，熵值越大，图像越复杂。

5. 计算单窗口所有统计方向对应的特征值后平均化

6. 计算整幅图像，重复步骤2-5

一个滑动窗口计算结束后，该窗口就可以移动一个像素点，形成另一个小窗口图像，重复进行上一步的计算，生成新窗口图像的共生矩阵和纹理特征值； 以此类推，滑动窗口遍历完所有的图像像素点后，整个图像就形成了一个由纹理特征值构成的一个纹理特征值矩阵。