分类器组合方法

前言

数据挖掘中有三项重要的工作：分类、聚类与关联分析，其中分类器是最为重要的应用。简单来讲，计算机获得一个对象的信息就能通过这些信息判断对象的类别。例如垃圾邮件过滤（判断一封邮件的类别是垃圾邮件还是非垃圾邮件）、手写识别（判断一个手写内容的类别是“1”还是其他）、人脸识别（判断一张图片的类别是包含人脸还是不包含人脸）。分类器可以由很多种算法完成，这篇文章主要希望讨论的是由民主投票能联系到的一个经典的分类算法。

民主投票

首先，我们需要看看在现实生活中的分类是如何完成的。假设我们需要投资买一支股票，显然我希望买到的股票能够价值上涨。在我对资本投资、股票市场一无所知的情况下，我应该如何才能够增加我盈利的可能性呢？很多聪明的人一定会想到去找专家，一般来讲专家的分析与判断比普通人更加可靠。但是，我们依然有问题，我们也不完全相信专家啊？其一，专家不是每次都能预测准确；其二，专家的水平参差不齐，遇到“砖家”那不就赔本了吗。那么，我们有一个最简单的方法就是找一群专家，通过投票决定我到底应该买那一支股票。这样应该就能提高我买中股票涨的可能性了吧？
现实生活中，这样的决策案例很多，大到选国家主席，小到竞选班长，我们都可以通过民主投票来完成。

民主投票的数学分析

民主投票在数学上能占得住脚吗？那么，我们就结合上例建立一个数学模型来分析。首先，问题简化为我已知一支股票，我请了n个专家来投票，投票的结果可能是涨或者跌（为了分析简单，我们不考虑持平的情况）。其次，我们来分析一下每个专家的预测准确性，我们假设第i个专家的预测准确性是p[i]。这群人可能有两种情况：1）有的人真的就是砖家，所以他们预测的准确性只有50%（瞎猜也能有一般概率猜中呀）；2）其中也有懂股票的人，所以他们的准确性p[i]<50%。最后，我们要分析一下n个专家的预测准确性了，根据民主投票的原则，我们认为超过半数的投票结果被认可，也就是说超过n/2个人选择涨，我们就认为股票预测结果为涨；否之为跌。那么整体预测的准确性如下式：

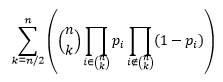
上式的含义是预测的准确性有多种情况，假设m=[n/2]+1(向下取整加1)，那么当k∈{m,m+1,…,n-1,n}时，恰好k个人认为这个股票会涨，则预测结果为涨。对于任意一个取值k，通过排列组合我们从n个人中找出k个人预测涨，n-k个人预测跌的概率。任意k对应的概率的求和则是整个专家团预测成功的概率。

这个公式的结果如何呢？让我们通过一些数据来验证一下：
情况1：假设我们的专家都挺靠谱，平均预测准确率（为了简化计算，我们假设所有准确率相同）为0.7，错误率为0.3，20个人的整体准确率为0.95。
情况2：假设我们的专家不怎么靠谱，平均预测准确率为0.55，错误率为0.45，20个人的整体准确率为0.59。
情况3：专家依然不靠谱但是我们人多，平均准确率为0.55，错误率为0.45，100个人的整体准确率为0.81。
总体来讲，整体的准确率肯定大于个体准确率，并且我们可以总结出两条规律：其一，专家准确率越高，最终结果准确率越高；其二，人数越多，准确率越高（前提条件是个体准确率大于瞎猜的准确率50%）。

分类器的组合方法

数学上证明了这条路是行得通的，于是计算机中就可以用这样的方法来做分类。为了时间和开销的考虑，我们可以选择很笨的基分类器（个体）但是计算机可以非常容易实现非常多的分类器组合。下面我们举一个案例来说明这个问题，假设我们需要通过一张图片来判断其中的人物的性别，我们可以用如下的方式来实现。
首先，我们需要利用数据挖掘、机器学习的方法来学习分类器（准确率不一定很高，但是要超过50%），例如：
基分类器1：长头发判断为女人、短头发判断为男人 - 准确率75%
基分类器2：穿靴子的是女人、穿运动鞋的是男人… - 准确率60%
基分类器3：穿裙子的是女人、否则是男人… - 准确率90%
基分类器4：背挎包的是女人、否则是男人… - 准确率70%
基分类器5：衣服为粉色的是女人、为黑色是男人… - 准确率60%
…

当我们有了无数分类器以后，一张图片输入，每个基分类器就能输出其对应的判断。通过投票我们就能得到准确率高的预测结果。

问题总结

民主投票其实是从小到大生活中的决策最常见的形式，可能很多人万万没有想到如此简单的判断方法居然能够解决机器学习、人工智能这样高大上的问题。其实，越是复杂的模型可能用越简单的方法反而有更好的结果。