过拟合与正则化

Location Beijing

过拟合

对于一个模型$A$，解向量空间为$\theta$，误差函数用式1表示
$$J(\theta )=J_{acc}=[y_{\theta }(x)-y{]}^2\text{\hspace{1em}(1)}$$
首先我们考虑用模型$A$拟合下图Fig. 1这些点（数据集）

Fig. 1 数据集

首先用一个模型去拟合这个曲线$y=a+bx+c{x}^2+d{x}^3$，可得如下图Fig. 2

Fig. 2 100%准确

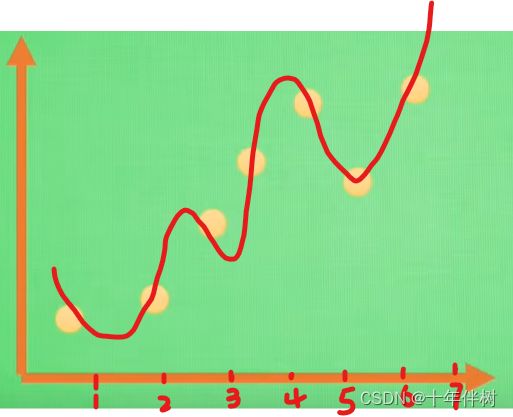
简直完美，因为误差$J(\theta )$=0。然而当我预测$x=4$的函数值时，发现预测值比真实值稍微大一丢丢，虽然感觉不对劲但是还可以接受；但当我预测$x=20$的函数值时，发现预测值大的离谱。
具体原因可以从上图Fig. 2看出，模型认为数据集中的点所有$x$及其对应的$y$都是百分百对应的，过分相信了数据集的准确性，忽略了数据集的误差。实际上可以看出，比如上图Fig. 2数据集中的$x=2$的点对应的函数值大概是$y=2$，然而数据集却把这一项标注成了$y=1$。模型A太厉害直接把带误差的数据集学透了。
这里也可以看出为什么说过拟合的表现是$J(\theta )$很小，但是预测新数据的能力很差，因为过拟合的模型太复杂，另外数据集标注太烂。

正则化

接下来看用正则化解决这个问题。
具体方法式在$J(\theta )$后面加一个正则化项，对于加入L1正则化的误差函数如公式2，加入L2正则化项的误差函数如公式3
$$J_{L1}(\theta )=J_{acc}+L_1=[y_{\theta }(x)-y{]}^2+[|{\theta }_1|+|{\theta }_2|..]\text{\hspace{1em}(2)}$$
$$J_{L2}(\theta )=J_{acc}+L_2=[y_{\theta }(x)-y{]}^2+[{\theta }_1^2+{\theta }_2^2+..]\text{\hspace{1em}(3)}$$
从公式2、3可以看出所谓正则化就是想以“牺牲”一些准确率的代价，来避免模型的复杂度。这里“牺牲”加引号的原因可以从第一章看出，这点损失的“准确率”事实上是象征着数据集的不准确性。让模型更有泛化能力。
至于为什么说L1正则化更容易得到稀疏的向量解空间，可以通过图Fig. 3看出，假设$\theta$是一个二维向量，包含两个元素{${\theta }_1$,${\theta }_2$}。（一个模型肯定不止两个参数，这里举两个参数的例子是比较好画）

Fig. 3 解空间

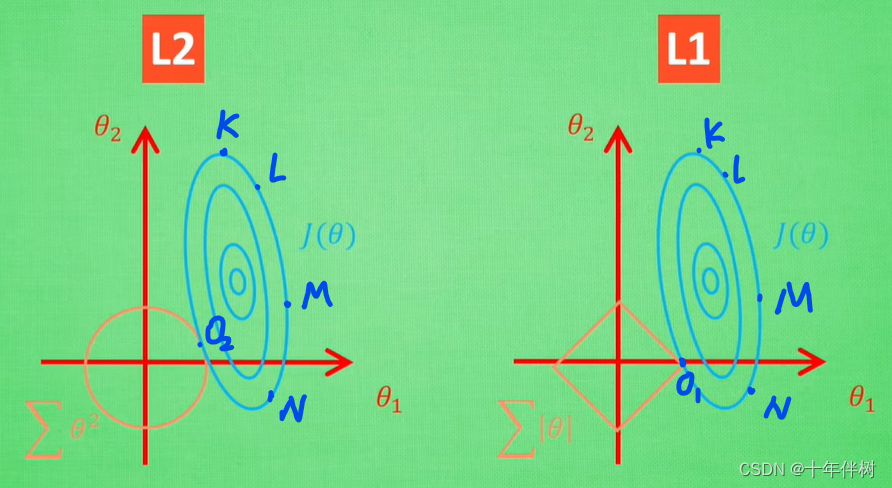
图Fig. 3中每个蓝色椭圆上的点表示不同的$\theta$使$J(\theta )$（注意不是$J_{acc}(\theta )$）相同的点。如点$K$,$L$,$M$,$N$,$O_2$是解空间$\theta$使含L2正则化项的误差函数$J_{L2}(\theta )$相同的点，这一批点中显然点$O_2$的L2正则化项最小；再比如点$K$,$L$,$M$,$N$,$O_1$是解空间$\theta$使含L1正则化项的误差函数$J_{L1}(\theta )$相同的点，这一批点中显然点$O_1$的L1正则化项最小。（从公式2、3可以看出，相同的$J(\theta )$，正则化项越小，$J_{acc}(\theta )$越大，所以尽量保留正则化较小的$\theta$解）
从这里可以看出L1正则化更容易使正则化项最小的同时，$J_{acc}(\theta )$最大，而且还带来了一个效果，由于L1正则化尖尖的探出的部分，更容易使$\theta$中的某一项为0，这就造成了L1正则化解空间的稀疏性。如果还想更稳妥，把这个正则化项改成非凸函数，特定情况下在成稀疏性的概率更大。
reference
[1] 莫烦Python 2017 什么是 L1 L2 正规化 正则化 Regularization (深度学习 deep learning)