已知 △ A B C \triangle ABC △ABC 的外心为 O O O, 其外接圆直径 M N MN MN 分别交 A B AB AB, A C AC AC 于点 E E E, F F F, E E E, F F F 关于 O O O 的对称点分别为 E 1 E_{1} E1, F 1 F_{1} F1. 求证: 直线 B F 1 BF_{1} BF1 与 C E 1 CE_{1} CE1 的交点在 △ A B C \triangle ABC △ABC 的外接圆上. (《高中数学联赛模拟试题精选》“学数学”系列第1套几何题)
证明:
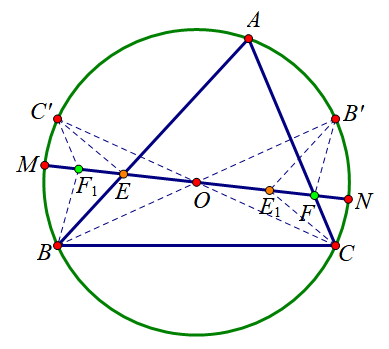
只需证明 ∠ E B F 1 = ∠ F C E 1 \angle EBF_1=\angle FCE_1 ∠EBF1=∠FCE1.
设 B B B, C C C 的对径点分别为点 B ′ B' B′, C ′ C' C′.
显然 △ C ′ F 1 E ≃ △ C F E 1 \triangle C'F_1E \simeq \triangle CFE_1 △C′F1E≃△CFE1, △ B ′ F E 1 ≃ △ B F 1 E \triangle B'FE_1 \simeq \triangle BF_1E △B′FE1≃△BF1E.
所以只需证明 ∠ E C ′ F = ∠ E 1 B ′ F \angle EC'F=\angle E_1B'F ∠EC′F=∠E1B′F.
延长 C ′ E C'E C′E 交 ( A B C ) (ABC) (ABC) 于点 K K K, 设 B ′ K B'K B′K 与 A C AC AC 交于点 F ′ F' F′.
由帕斯卡定理, A B AB AB 与 C ′ K C'K C′K 的交点 E E E, A C AC AC 与 B ′ K B'K B′K 的交点 F ′ F' F′, 与 C C ′ CC' CC′ 与 B B ′ BB' BB′ 的交点 O O O 三点共线, 由此可知 F ′ F' F′ 即为点 F F F.
∠ E B F 1 = ∠ F C E 1 \angle EBF_1=\angle FCE_1 ∠EBF1=∠FCE1.
设 A A A 的对径点为点 A ′ A' A′, 设 C ′ A ′ C'A' C′A′ 交直线 E F EF EF 于点 F 1 ′ F_1' F1′, B ′ A ′ B'A' B′A′ 交直线 E F EF EF 于点 E 1 ′ E_1' E1′.
显然 ∠ O C ′ F 1 ′ = ∠ O C F \angle OC'F_1'=\angle OCF ∠OC′F1′=∠OCF, ∠ C ′ O F 1 ′ = ∠ C O F \angle C'OF_1'=\angle COF ∠C′OF1′=∠COF, O C ′ = O C OC'=OC OC′=OC, 所以 △ O C ′ F 1 ′ ≃ △ O C F \triangle OC'F_1' \simeq \triangle OCF △OC′F1′≃△OCF. 由此可知 O F 1 ′ = O F OF_1'=OF OF1′=OF, F 1 ′ F_1' F1′ 即为 F 1 F_1 F1.
同理, E 1 ′ E_1' E1′ 即为 E 1 E_1 E1.
由 C ′ C' C′, B ′ B' B′, K K K, A ′ A' A′ 共圆可知 ∠ E C ′ F 1 = ∠ F B ′ E 1 \angle EC'F_1=\angle FB'E_1 ∠EC′F1=∠FB′E1.
证毕.
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
