kaggle项目之:Titanic Data Science Solutions

已于 2025-04-18 08:41:21 修改
阅读量424 收藏 4
点赞数 3
分类专栏： python数据分析 文章标签： python pandas 随机森林 机器学习
于 2025-04-18 02:26:50 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Jmayday/article/details/147316480
版权

        开发工具:Anaconda

        kaggle的项目地址:https://www.kaggle.com/code/startupsci/titanic-data-science-solutions

 第一部分    导入数据

目标:导入项目所依赖的包、训练以及测试数据、熟悉数据。

代码如下:

# 数据分析模块依赖的包
import pandas as pd
import numpy as np
import random as rnd

# 可视化
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

# 机器学习
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier

train_df = pd.read_csv(r'E:/train.csv')
test_df = pd.read_csv(r'E:/test.csv')

# 注释:
# PassengerId：乘客编号
# Survived：生存状态（0代表未存活，1代表存活）
# Pclass：舱位等级
# Name：乘客姓名
# Sex：性别
# Age：年龄
# SibSp：同舱兄弟姐妹或配偶的数量
# Parch：同行父母或子女的数量
# Ticket：票号
# Fare：票价
# Cabin：舱位
# Embarked：登船港口

2、熟悉导入的数据

train_df.head()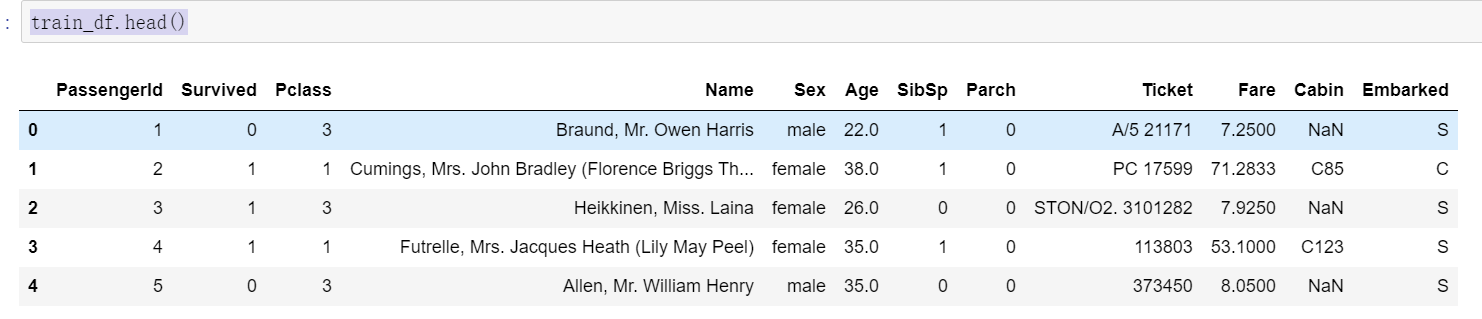

train_df.describe(include="all")

 

test_df.head()

 

test_df.describe(include='all')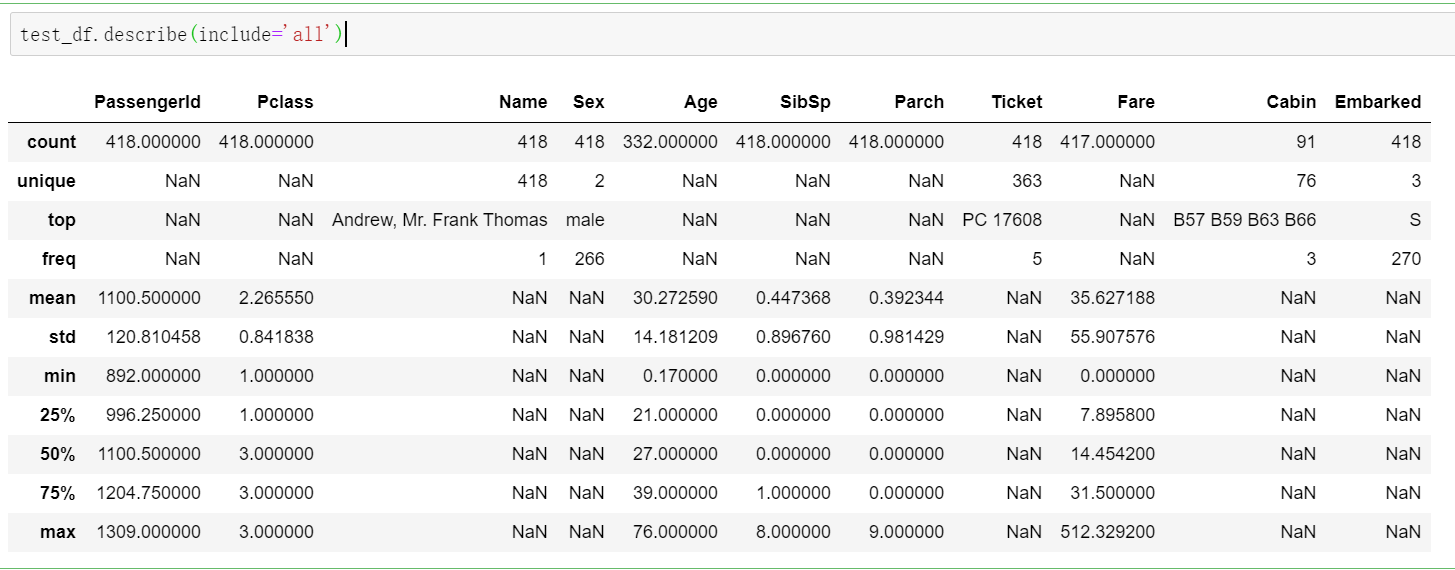

# 把数据形成一个列表
combine = [train_df,test_df]

# 打印一下字段名称
print(train_df.columns.values)

# 如何选择合适的特性进行分析，首先要了解数据我类型以及是否存在空值
train_df.info()
print("-"*40)
test_df.info()

 

train_df.describe(include=['O'])

 

2、对数据进行统计分析

# 分析各及等仓的平均求生概率

# 先将要聚合的字段转换为int型，不然执行会报错，如果导入的int型就不用转换
train_df.info()
train_df[['Pclass', 'Survived']].groupby(['Pclass'], as_index=False).mean().sort_values(by='Survived', ascending=False)

 

# 计算不同性别获救的概率

# 参数说明
# as_index=False提高代码效率，避免索引引起的复杂计算
# ascending=False降序排列

train_df[["Sex", "Survived"]].groupby(['Sex'], as_index=False).mean().sort_values(by='Survived', ascending=False)

 

# 计算同舱有兄弟姐妹及配偶的获救概率
train_df[["SibSp", "Survived"]].groupby(['SibSp'], as_index=False).mean().sort_values(by='Survived', ascending=False)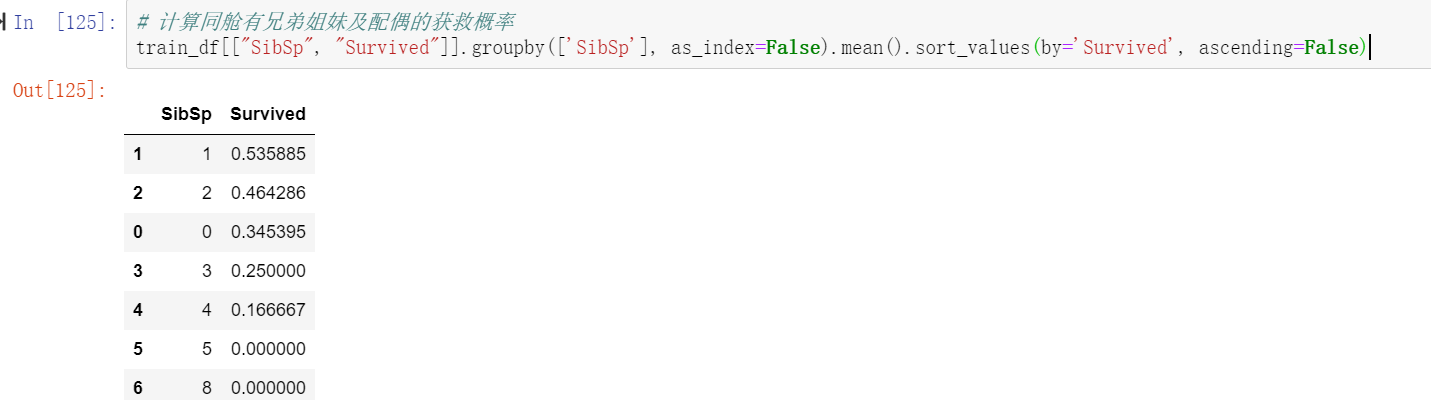

 

# 计算同舱有父母或者子女的获救概率

train_df[["Parch", "Survived"]].groupby(['Parch'], as_index=False).mean().sort_values(by='Survived', ascending=False)

 

第二部分:可视化分析 

目标：通过一些可视化图表分析数据特征及关联关系

# 可视化分析
#1、考虑不同年龄对模型的影响
# 说明:但是之前熟悉数据可以知道年龄数据是有缺失的，只有700多条可能会对分析产生影响
# 用直方图来展示获救和未获救的乘客年龄分布

# 说明:
# bins=20:直方图中分为20个箱子
g = sns.FacetGrid(train_df, col='Survived')
g.map(plt.hist, 'Age', bins=20)

运行结果如下:

# 2、考虑不同客舱等级因素对模型的影响
# 我们可以结合多个特征，通过单一图表来识别它们之间的相关性。这可以应用于具有数值的数值型特征和分类型特征。

# grid = sns.FacetGrid(train_df, col='Pclass', hue='Survived')
grid = sns.FacetGrid(train_df, col='Survived', row='Pclass', size=2.2, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend();

 

# 3、考虑不同登机口对模型的影响

grid = sns.FacetGrid(train_df, row='Embarked', size=2.2, aspect=1.6)
grid.map(sns.pointplot, 'Pclass', 'Survived', 'Sex', palette='deep')
grid.add_legend()

 运行结果如下:

# 4、考虑票价对模型的影响
# 我们可能还希望分析分类特征（具有非数值型值）和数值型特征之间的相关性。我们可以考虑将登船港口（分类非数值型）、
# 性别（分类非数值型）、票价（数值型连续变量）与是否存活（分类数值型）这些特征进行相关性分析。

train_df["Fare"]=train_df["Fare"].astype(float)
grid = sns.FacetGrid(train_df, row='Embarked', col='Survived', size=2.2, aspect=1.6)
grid.map(sns.barplot, 'Sex', 'Fare', alpha=.5, ci=None)
grid.add_legend()

 运行结果如下:

"""
我们已经收集了一些关于数据集和解决方案要求的假设和决策。到目前为止，我们还无需更改任何一个特征或值就能得出这些结论。
现在，让我们执行我们的决策和假设，以实现纠正、创建和完善数据的目标。
通过删除特征进行纠正
这是一个很好的起始目标。通过删除特征，我们处理的数据点会更少。这样可以加快我们的笔记本运行速度，并简化分析过程。
基于我们的假设和决策，我们希望删除 “客舱”（纠正目标 2）和 “票号”（纠正目标 1）这两个特征。
"""
# 说明:
# 比较明显的对比处理前后字段的个数的变化
print("Before", train_df.shape, test_df.shape, combine[0].shape, combine[1].shape)

train_df = train_df.drop(['Ticket', 'Cabin'], axis=1)
test_df = test_df.drop(['Ticket', 'Cabin'], axis=1)
combine = [train_df, test_df]

"After", train_df.shape, test_df.shape, combine[0].shape, combine[1].shape

运行结果如下:

 第三部分    数据特性处理

目标:将字符串属性处理为数值型加入模型训练，并且合并关联特性

# 4、将新特性加入模型训练
# 将名字分类加入模型训练


# 顺便复习一下正则表达式
"""
正则表达式语法元素解析
1. [A-Za-z]
这是一个字符类，用于匹配方括号内指定范围的任意单个字符。
A-Z 表示匹配从大写字母 A 到 Z 之间的任意一个大写字母。
a-z 表示匹配从小写字母 a 到 z 之间的任意一个小写字母。
结合起来，[A-Za-z] 就能匹配任意一个英文字母（包括大写和小写）。
2. +
这是一个量词，用于指定前面的元素（这里是字符类 [A-Za-z]）出现的次数。+ 表示前面的元素至少出现一次，最多可以出现无限次。
所以 [A-Za-z]+ 表示匹配由一个或多个英文字母组成的字符串。
3. \.
在正则表达式里，点号 . 是一个特殊字符，它默认匹配除换行符之外的任意单个字符。若要匹配真正的点号，
就需要使用反斜杠 \ 对其进行转义，即 \. 表示匹配一个实际的点号字符。

"""

for dataset in combine:
    dataset['Title'] = dataset.Name.str.extract(' ([A-Za-z]+)\.', expand=False)

pd.crosstab(train_df['Title'], train_df['Sex'])

运行结果如下:

# 将比较少见的归为一类rare

for dataset in combine:
    dataset['Title'] = dataset['Title'].replace(['Lady', 'Countess','Capt', 'Col',\
 	'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')

    dataset['Title'] = dataset['Title'].replace('Mlle', 'Miss')
    dataset['Title'] = dataset['Title'].replace('Ms', 'Miss')
    dataset['Title'] = dataset['Title'].replace('Mme', 'Mrs')
    
train_df[['Title', 'Survived']].groupby(['Title'], as_index=False).mean()

 运行结果如下:

# 查看处理后的数据多了Title列
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
for dataset in combine:
    dataset['Title'] = dataset['Title'].map(title_mapping)
    dataset['Title'] = dataset['Title'].fillna(0)

train_df.head()

 运行结果如下:

# 继续将一些用不到的字段特性处理掉
train_df = train_df.drop(['Name', 'PassengerId'], axis=1)
test_df = test_df.drop(['Name'], axis=1)
combine = [train_df, test_df]
train_df.shape, test_df.shape

 

# 5、将性别特性处理一下

for dataset in combine:
    dataset['Sex'] = dataset['Sex'].map( {'female': 1, 'male': 0} ).astype(int)

train_df.head()

运行结果如下: 

 

"""
我们可以考虑三种方法来完善一个数值型连续特征。
一种简单的方法是生成介于均值和标准差之间的随机数。
一种更准确地猜测缺失值的方法是使用其他相关特征。在我们的例子中，我们注意到 “年龄”（Age）、“性别”（Gender）和 
“客舱等级”（Pclass）之间存在相关性。通过 “客舱等级”（Pclass）和 “性别”（Gender）特征组合的不同集合中年龄的中位数来猜测年龄值。
也就是说，对于 “客舱等级”（Pclass）=1 且 “性别”（Gender）=0、“客舱等级”（Pclass）=1 且 “性别”（Gender）=1 等等这些组合，
使用相应的年龄中位数……
将方法 1 和方法 2 结合起来。所以，不是基于中位数来猜测年龄值，而是根据 “客舱等级”（Pclass）
和 “性别”（Gender）的不同组合集合，使用介于均值和标准差之间的随机数。
方法 1 和方法 3 会给我们的模型引入随机噪声。多次执行的结果可能会有所不同。我们更倾向于使用方法 2。
"""

# grid = sns.FacetGrid(train_df, col='Pclass', hue='Gender')
grid = sns.FacetGrid(train_df, row='Pclass', col='Sex', size=2.2, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend()

 运行结果如下:

# 让我们从准备一个空数组开始，这个数组用于存放根据客舱等级（Pclass）和性别（Gender）组合所推测出的年龄值。

guess_ages = np.zeros((2,3))
guess_ages

运行结果如下: 

 

# 现在，我们要对性别（取值为 0 或 1）和客舱等级（取值为 1、2、3）进行遍历，以计算这六种组合情况下推测的年龄值。
for dataset in combine:
    for i in range(0, 2):
        for j in range(0, 3):
            guess_df = dataset[(dataset['Sex'] == i) & \
                                  (dataset['Pclass'] == j+1)]['Age'].dropna()

            # age_mean = guess_df.mean()
            # age_std = guess_df.std()
            # age_guess = rnd.uniform(age_mean - age_std, age_mean + age_std)

            age_guess = guess_df.median()

            # Convert random age float to nearest .5 age
            guess_ages[i,j] = int( age_guess/0.5 + 0.5 ) * 0.5
            
    for i in range(0, 2):
        for j in range(0, 3):
            dataset.loc[ (dataset.Age.isnull()) & (dataset.Sex == i) & (dataset.Pclass == j+1),\
                    'Age'] = guess_ages[i,j]

    dataset['Age'] = dataset['Age'].astype(int)

train_df.head()

 运行结果如下:

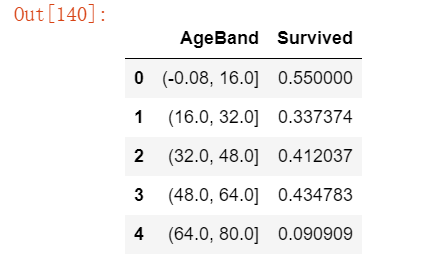
# 研究年龄区间与存活率的关系

# 将年龄划分为五个等宽区间
train_df['AgeBand'] = pd.cut(train_df['Age'], 5)

# 计算每个年龄区间的平均存活概率
train_df[['AgeBand', 'Survived']].groupby(['AgeBand'], as_index=False).mean().sort_values(by='AgeBand', ascending=True)

 运行结果如下:

# 用序数来代替年龄区间
for dataset in combine:    
    dataset.loc[ dataset['Age'] <= 16, 'Age'] = 0
    dataset.loc[(dataset['Age'] > 16) & (dataset['Age'] <= 32), 'Age'] = 1
    dataset.loc[(dataset['Age'] > 32) & (dataset['Age'] <= 48), 'Age'] = 2
    dataset.loc[(dataset['Age'] > 48) & (dataset['Age'] <= 64), 'Age'] = 3
    dataset.loc[ dataset['Age'] > 64, 'Age']
train_df.head()

运行结果如下:

# 将年龄区间删除，观察数据的特点
train_df = train_df.drop(['AgeBand'], axis=1)
combine = [train_df, test_df]
train_df.head()

 运行结果如下:

# 接下来将分类相近的亲属关系的两个特性结合形成一个新的特性
for dataset in combine:
    dataset['FamilySize'] = dataset['SibSp'] + dataset['Parch'] + 1

train_df[['FamilySize', 'Survived']].groupby(['FamilySize'], as_index=False).mean().sort_values(by='Survived', ascending=False)

 运行结果如下:

# 再次处理形成新的特性
for dataset in combine:
    dataset['IsAlone'] = 0
    dataset.loc[dataset['FamilySize'] == 1, 'IsAlone'] = 1

train_df[['IsAlone', 'Survived']].groupby(['IsAlone'], as_index=False).mean()

 运行结果如下:

# 只保留我们处理后的特性
train_df = train_df.drop(['Parch', 'SibSp', 'FamilySize'], axis=1)
test_df = test_df.drop(['Parch', 'SibSp', 'FamilySize'], axis=1)
combine = [train_df, test_df]

train_df.head()

 运行结果如下:

# 创建一个结合舱位级别和年龄的特性
for dataset in combine:
    dataset['Age*Class'] = dataset.Age * dataset.Pclass

train_df.loc[:, ['Age*Class', 'Age', 'Pclass']].head(10)

 运行结果如下:

# 完成分类特征 ¶Embarked 特征根据登船港取 S、Q、C 值。我们的训练集有两个缺失值。我们简单地用最常见的情况填充这些。

freq_port = train_df.Embarked.dropna().mode()[0]
freq_port

 

for dataset in combine:
    dataset['Embarked'] = dataset['Embarked'].fillna(freq_port)
    
train_df[['Embarked', 'Survived']].groupby(['Embarked'], as_index=False).mean().sort_values(by='Survived', ascending=False)

 运行结果如下:

# 将分类特征转换为数字特征。现在我们可以通过创建一个新的数字特征 “Port” 来转换 “EmbarkedFill” 特征。
for dataset in combine:
    dataset['Embarked'] = dataset['Embarked'].map( {'S': 0, 'C': 1, 'Q': 2} ).astype(int)

train_df.head()

 运行结果如下:

# 我们现在可以使用众数来完成测试数据集中单个缺失值的 “票价” 特征
test_df['Fare'].fillna(test_df['Fare'].dropna().median(), inplace=True)
test_df.head()

 运行结果如下：

#  创建一个票价区间
train_df['FareBand'] = pd.qcut(train_df['Fare'], 4)
train_df[['FareBand', 'Survived']].groupby(['FareBand'], as_index=False).mean().sort_values(by='FareBand', ascending=True)

运行结果如下： 

# 用序数代替区间
for dataset in combine:
    dataset.loc[ dataset['Fare'] <= 7.91, 'Fare'] = 0
    dataset.loc[(dataset['Fare'] > 7.91) & (dataset['Fare'] <= 14.454), 'Fare'] = 1
    dataset.loc[(dataset['Fare'] > 14.454) & (dataset['Fare'] <= 31), 'Fare']   = 2
    dataset.loc[ dataset['Fare'] > 31, 'Fare'] = 3
    dataset['Fare'] = dataset['Fare'].astype(int)

train_df = train_df.drop(['FareBand'], axis=1)
combine = [train_df, test_df]
    
train_df.head(10)

 运行结果如下:

test_df.head(10)

 

第四部分    机器学习解决方案 

目标:探索最优模型解决方案

# 我们要选择模型来预测解决，下面是一些用到的模型
"""
我们还在执行一种机器学习类别，称为监督学习，因为我们正在使用给定的数据集训练我们的模型。
有了这两个标准 —— 监督学习加上分类和回归，我们可以将模型的选择范围缩小到几个。这些包括：
・逻辑回归
・KNN 或 k 近邻
・支持向量机
・朴素贝叶斯分类器
・决策树
・随机森林
・感知机

"""

#  将train_df中的survived删除并删除乘客ID
X_train = train_df.drop("Survived", axis=1)
Y_train = train_df["Survived"]
X_test  = test_df.drop("PassengerId", axis=1).copy()
X_train.shape, Y_train.shape, X_test.shape

运行结果如下： 

# 逻辑回归通过使用逻辑函数（即累积逻辑分布）估计概率来衡量分类
# 因变量（特征）与一个或多个自变量（特征）之间的关系。
logreg = LogisticRegression()
logreg.fit(X_train, Y_train)
Y_pred = logreg.predict(X_test)
acc_log = round(logreg.score(X_train, Y_train) * 100, 2)
acc_log

 运行结果如下：

"""
我们可以使用逻辑回归来验证我们在特征创建和完成目标方面的假设和决策。
这可以通过计算决策函数中特征的系数来实现。
正系数会增加响应的对数几率（从而增加概率），负系数会降低响应的对数几率（从而降低概率）。
・性别具有最高的正系数，
这意味着随着性别值的增加（男性：0 到女性：1），生存概率为 1 的概率增加最多。
・相反，随着客舱等级（Pclass）的增加，
生存概率为 1 的概率下降最多。・这样一来，年龄 × 客舱等级（Age*Class）是
一个很好的人工特征模型，因为它与生存概率的负相关性排名第二。
・头衔（Title）也是具有第二高正相关性的特征。
"""

coeff_df = pd.DataFrame(train_df.columns.delete(0))
coeff_df.columns = ['Feature']
coeff_df["Correlation"] = pd.Series(logreg.coef_[0])

coeff_df.sort_values(by='Correlation', ascending=False)

 运行结果如下;

"""
接下来我们使用支持向量机进行建模，支持向量机是有相关学习算法的监督学习模型，
用于分析用于分类和回归分析的数据。
给定一组训练样本，每个样本都被标记为属于两个类别中的一个，
支持向量机训练算法构建一个模型，将新的测试样本分配到一个类别或另一个类别，
使其成为一个非概率二元线性分类器。参考维基百科。

"""

# 支持向量机
svc = SVC()
svc.fit(X_train, Y_train)
Y_pred = svc.predict(X_test)
acc_svc = round(svc.score(X_train, Y_train) * 100, 2)
acc_svc

 运行结果如下：

"""
在模式识别中，k 近邻算法（简称 k-NN）是一种用于分类和回归的非参数方法。
样本通过其邻居的多数投票进行分类，
样本被分配到其 k 个最近邻居中最常见的类别（k 是一个正整数，通常较小）。
如果 k = 1，那么对象就简单地被分配到那个单个最近邻居的类别。
参考维基百科。KNN 的置信度得分优于逻辑回归，但不如支持向量机。

"""

# k近邻算法
knn = KNeighborsClassifier(n_neighbors = 3)
knn.fit(X_train, Y_train)
Y_pred = knn.predict(X_test)
acc_knn = round(knn.score(X_train, Y_train) * 100, 2)
acc_knn

运行结果如下：

"""
在机器学习中，朴素贝叶斯分类器是一类简单的概率分类器，基于应用贝叶斯定理，
并在特征之间做出强（朴素）独立性假设。
朴素贝叶斯分类器具有高度可扩展性，在学习问题中所需的参数数量与
变量（特征）数量呈线性关系。参考维基百科。到目前为止评估的模型中，
该模型生成的置信度得分是最低的。
"""

# 贝叶斯算法
gaussian = GaussianNB()
gaussian.fit(X_train, Y_train)
Y_pred = gaussian.predict(X_test)
acc_gaussian = round(gaussian.score(X_train, Y_train) * 100, 2)
acc_gaussian

 运行结果如下： 

"""
感知机是一种用于二元分类器有监督学习的算法（能够确定由数字向量
表示的输入是否属于某个特定类别的函数）。
它是一种线性分类器，即一种基于线性预测函数进行预测的分类算法，该函数将
一组权重与特征向量相结合。该算法允许在线学习，
因为它一次处理训练集中的一个元素。

"""

perceptron = Perceptron()
perceptron.fit(X_train, Y_train)
Y_pred = perceptron.predict(X_test)
acc_perceptron = round(perceptron.score(X_train, Y_train) * 100, 2)
acc_perceptron

运行结果如下：

linear_svc = LinearSVC()
linear_svc.fit(X_train, Y_train)
Y_pred = linear_svc.predict(X_test)
acc_linear_svc = round(linear_svc.score(X_train, Y_train) * 100, 2)
acc_linear_svc

 运行结果如下：

sgd = SGDClassifier()
sgd.fit(X_train, Y_train)
Y_pred = sgd.predict(X_test)
acc_sgd = round(sgd.score(X_train, Y_train) * 100, 2)
acc_sgd

运行结果如下： 

"""
该模型使用决策树作为预测模型，将特征（树分支）映射到关于目标值（树叶子）的结论。
目标变量可以取有限个值的树模型称为分类树；在这些树结构中，叶子代表类别标签，
分支代表导致这些类别标签的特征的合取。
目标变量可以取连续值（通常是实数）的决策树称为回归树。

"""

decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train, Y_train)
Y_pred = decision_tree.predict(X_test)
acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2)
acc_decision_tree

 运行结果如下:

# 随机森林

"""
随机森林或随机决策森林是一种用于分类、回归和其他任务的集成学习方法，
它通过在训练时构建大量决策树（n_estimators=100）
并输出作为各个树的类别众数（分类）或平均预测（回归）的类别来进行操作。

"""

random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
Y_pred = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)
acc_random_forest

运行结果如下： 

# 模型评估 我们现在可以对所有模型的评估进行排序，以选择最适合我们问题的模型。
# 虽然决策树和随机森林的得分相同，
# 但我们选择使用随机森林，因为它们可以纠正决策树过度拟合训练集的习惯。

models = pd.DataFrame({
    'Model': ['Support Vector Machines', 'KNN', 'Logistic Regression', 
              'Random Forest', 'Naive Bayes', 'Perceptron', 
              'Stochastic Gradient Decent', 'Linear SVC', 
              'Decision Tree'],
    'Score': [acc_svc, acc_knn, acc_log, 
              acc_random_forest, acc_gaussian, acc_perceptron, 
              acc_sgd, acc_linear_svc, acc_decision_tree]})
models.sort_values(by='Score', ascending=False)

 运行结果如下:

# 对比发现随机森林的置信度最高，所以将模型数据保存
submission = pd.DataFrame({
        "PassengerId": test_df["PassengerId"],
        "Survived": Y_pred
    })
# submission.to_csv('../output/submission.csv', index=False)

    以上就是在kaggle上的第二个数据分析项目，大致可以帮助我们了解一下数据分析的大致流程，加强数据处理能力以及思维，最后通过各个模型测试对比得出最优的模型。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值