51nod 1627 瞬间移动 组合数取模

关于组合数取模和逆元的知识的参考
http://blog.csdn.net/acdreamers/article/details/8037918
http://blog.csdn.net/acdreamers/article/details/8220787#comments
题目：
有一个无限大的矩形，初始时你在左上角（即第一行第一列），每次你都可以选择一个右下方格子，并瞬移过去（如从下图中的红色格子能直接瞬移到蓝色格子），求到第n行第m列的格子有几种方案，答案对1000000007取模。

Input
单组测试数据。
两个整数n,m（2<=n,m<=100000）
Output
一个整数表示答案。
Input示例
4 5
Output示例
10
可通过打表或者其他理解得出
答案为C(m+n-4，m-2)或C(m+n-4，n-2)//可优化的地方

#include <iostream>
#include <cstdio>
#include <sstream>
#include <set>
#include <bitset>  
#include <queue>  
#include <stack> 
#include <list>
#include <vector>
#include <map>
#include <string>
#include <cstring>
#include <cmath>
#include <algorithm>

using namespace std;
typedef set<int> Set;
typedef vector<int> Vec;
typedef set<int>::iterator It;
typedef long long ll;
#define mem(s,n) memset(s,n,sizeof(s))

int p = 1000000007;

ll quick_mod(ll a,ll b)//a^b%p 快速幂
{
    ll ans = 1;
    a %= p;
    while(b)
    {
        if(b & 1)
        {
            ans = ans * a % p;
            b--;
        }       
        b >>= 1;
        a = a * a % p;  
    }
    return ans; 
}

ll C(ll n,ll m)//nCm %p
{
    if(n < m)   return 0;
    ll ans = 1;
    for(ll i=1;i<=m;i++)    
    {
        ll a = (n - m + i) % p;
        ll b = i % p;
        ans = ans *(a * quick_mod(b,p-2) % p) % p;//逆元的知识 
    }
    return ans;
}

ll Lucas(ll n,ll m)//Lucas定理
{
    if(m == 0) return 1;
    return C(n % p,m % p) * Lucas(n / p,m / p) % p;
}

int main(int argc, char *argv[])
{
    ll m,n,a,b;
    scanf("%lld%lld",&m,&n);
    b=m+n-4;
    a=min(m-2,n-2);
    printf("%lld\n",Lucas(b,a));
    return 0;
}

对于正整数 a 和 p,若 ax≡1 mod p, 则称a关于模f的乘法逆元为x。
也可表示为ax≡1(mod p)。逆元一般用扩展欧几里得算法来求得，如果为素数，那么还可以根据费马小定理得到逆元为
$a^{p-2}≡\frac{1}{a}$(mod p)
实际应用主要用于处理除法取模 如组合数

和且p为素数
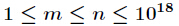
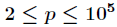
Lucas定理：

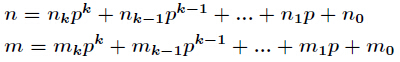
则有

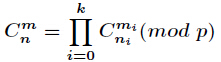
利用逆元计算即可

对于逆元和Lucas定理的理解还很浅显 需要更深入去了解