判断二叉树是否为平衡二叉树

题目：
输入一颗二叉树的根节点，判断该树是不是平衡二叉树。

1.平衡二叉树

定义：一棵空树或它的任意节点的左右两个子树的高度差的绝对值均不超过1。

下面就是一颗平衡二叉树：

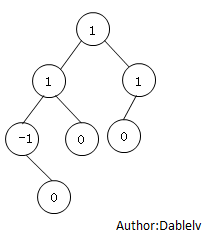
2.解法一

解题思路：
根据二叉树的定义，我们可以递归遍历二叉树的每一个节点来，求出每个节点的左右子树的高度，如果每个节点的左右子树的高度相差不超过1，按照定义，它就是一颗平衡二叉树。

参考如下代码：

//求二叉树的高度
int treeDepth(BinaryTreeNode* root){
    if(root==NULL){
        return 0;
    }
    int nLeft=treeDepth(root->m_pLeft);
    int nRight=treeDepth(root->m_pRight);
    return nLeft>nRight?nLeft+1:nRight+1;
}

bool isBalanced(BinaryTreeNode* root){
    if(root==NULL)
        return true;//空树是平衡二叉树
    int left= treeDepth(root->m_pLeft);
    int right= treeDepth(root->m_pRight);
    int diff=left-right;
    if(diff>1||diff<-1)
        return false;
    return isBalanced(root->m_pLeft)&&isBalanced(root->m_pRight);
}

优点：只要求出给定二叉树的高度，就可以方便的判断出二叉树是平衡二叉树，思路简单，代码简洁。

缺点：由于每个节点都会被重复遍历多次，这造成时间效率不高。例如在上面的函数输入isBalanced()函数中输入如下二叉树：

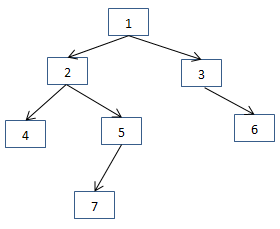
我们首先判断根节点1是不是平衡的，此时我们需要调用treeDepth()函数求根节点左子树的高度，需要遍历节点4、5、7。接下来需要判断以节点2为根节点的子树是不是平衡树的时候，分别求以节点2为根节点的左子树的高度和右子树的高度，这时又遍历了节点4、5、7。

很显然，节点的重复遍历会造成性能的下降，下面将给出每个节点只遍历一次的解法。

2.解法二

解题思路：
采用后序遍历的方式遍历二叉树的每一个节点，在遍历到一个节点之前我们就已经遍历了它的左右字数。此时，记录每个节点为根节点的树的高度，就可以一边遍历一边判断每个节点是不是平衡的。

参考代码：

bool IsBalanced(BinaryTreeNode* pRoot, int* depth){  
    if(pRoot== NULL){  
        *depth = 0;  
        return true;  
    }  

    int nLeftDepth,nRightDepth;  
    bool bLeft= IsBalanced(pRoot->m_pLeft, &nLeftDepth);  
    bool bRight = IsBalanced(pRoot->m_pRight, &nRightDepth);  

    if (bLeft && bRight){  
        int diff = nRightDepth-nLeftDepth;  
        if (diff<=1 && diff>=-1) //左右字树高度差绝对值不超过1  
        {  
            *depth = 1+(nLeftDepth > nRightDepth ? nLeftDepth : nRightDepth);  
            return true;  
        }  
    }   
    return false;  
}  

bool IsBalanced(BinaryTreeNode* pRoot)  
{  
    int depth = 0;  

    return IsBalanced(pRoot, &depth);  
}  

---

参考文献

[1]http://blog.csdn.net/k346k346/article/details/51076268.
[2]剑指Offer.何海涛.电子工业出版社.