文章目录
前言:
前面介绍了直接插入排序,
希尔排序是希尔(Donald Shell)于1959年提出的一种排序算法。希尔排序也是一种插入排序
是直接插入排序的优化!
这个优化可以说是 十分NB的!
希尔排序算法思想
希尔排序又叫缩小增量法
基本思想是:先选定一个整数gap,然后把待排序数据中的数据分为gap组,所以距离为gap的数据为一组,并且对每一组的数据分别进行插入排序。然后缩小gap,重复上面的工作,直到gap缩小为1,进行最后一次,也就是直接插入排序(gap==1时)
其实gap等于1之前的操作,叫做:分组插入预排
希尔排序分为两步
- 预排序(接近顺序有序)
- 直接插入排序(有序)
预排:类插入排序
end标识每组第一个数据,不过end一次走gap步而不是走1步- 拿到
end+gap处的数据tmp,然后与end处比较,如果end处的数据大于tmp,end处的数据挪动到end+gap处,然后end向前走gap步找前一个 - 直到
end<0或者end处的数据小于等于tmp,循环跳出 - 然后把
end+gap处的数据赋值为tmp end到下一个位置重复上面过程
如图的例子

希尔排序图解
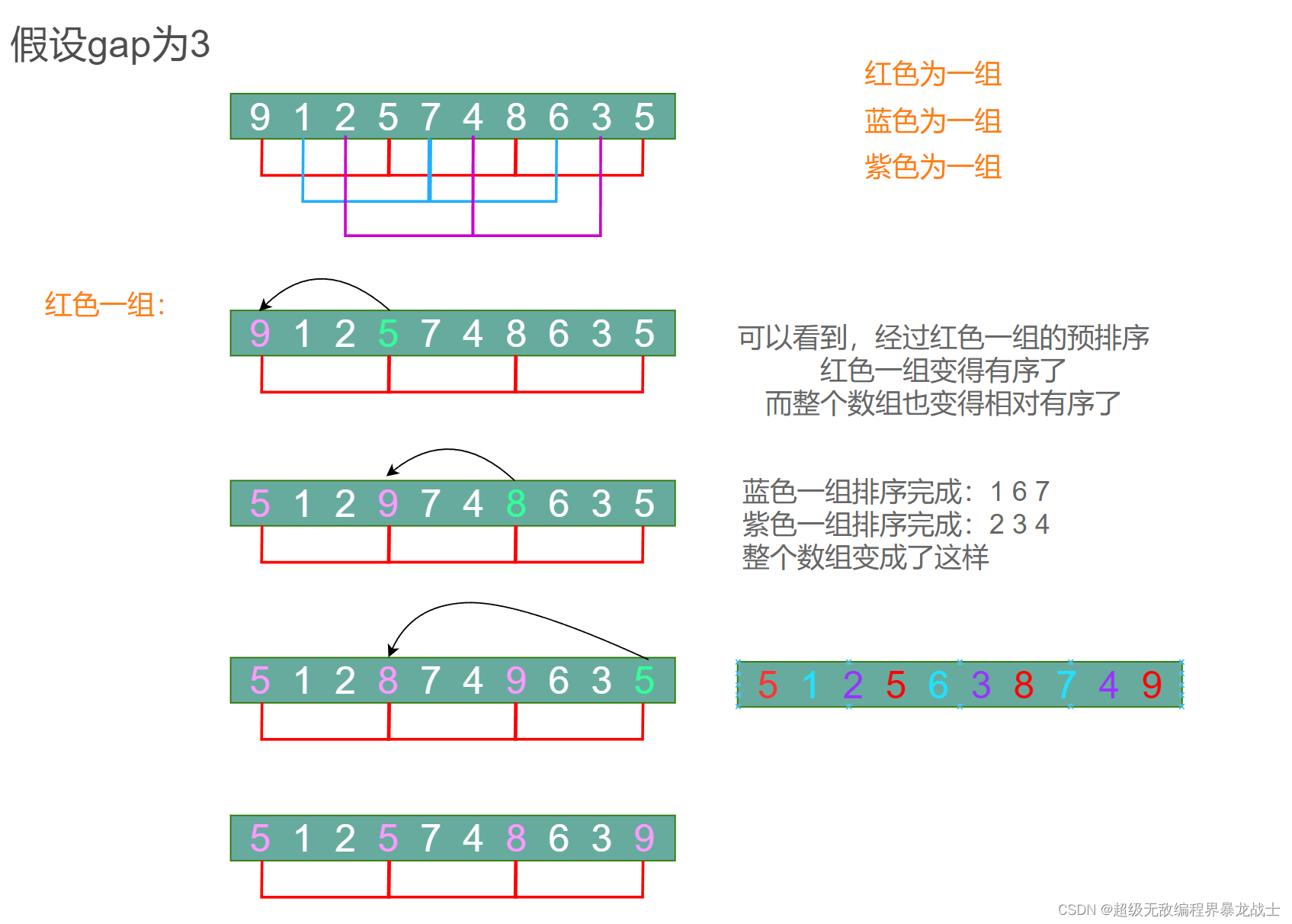
可以看到,其实分组预排之后数组已经接近有序了
分组预排就是给插入排序作准备工作的!
而分组预排的消耗并不是很大,因为gap的原因,不会像直接插入排序那样挨个的比较
同一组的相邻数据相隔gap步
关于gap的取值

分析
gap不能太大也不能太小,一般与n有关并且是动态变化的
如果数据量比较大 如 n=10000
-
那么可以让
gap=n,然后每一次进入循环都除3 (gap/=3)
这样gap就等于 3333 --> 1111 ->…
gap是可变的,有大有小,并且/=3为条件,是指数级的缩小
既保证了预排的有限次
又保证了预排的效率性(接近顺序有序) -
gap如果很小取一个定值,那么前面的数经过很多次才可以到后面去,太小就和直接插入排序差不多了,而gap很大排的次数又很少,效果差。
结论:一般采用两种方法
gap=n
每一次进入循环gap=gap/3+1
这样保证了gap从大到小的变化,并且+1保证了最后一次一定是1(直接插入排序)gap=n
每一次进入循环gap=gap/2
因为除2 最后总会是1,所以可以不用+1
C参考代码
void ShellSort(int *a, int n)
{
int gap = n;
//gap : 4--2--1
while (gap > 1)
{
//当gap/3==0 然后在+1 下一次就会他来到上面就会跳出循环
gap = gap / 3+1;//最后gap一定为1 也就是控制了插入排序
for (int i = 0; i < n - gap; ++i)
{
//一次希尔排序
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;//每一次找前一个是向前gap步
}
else
{
break;
}
}
//跳出循环之后
a[end + gap] = tmp;
}
}
}
时间复杂度分析*
关于希尔排序的时间复杂度一直是一个争议的问题
因为它着实不好算!
分析
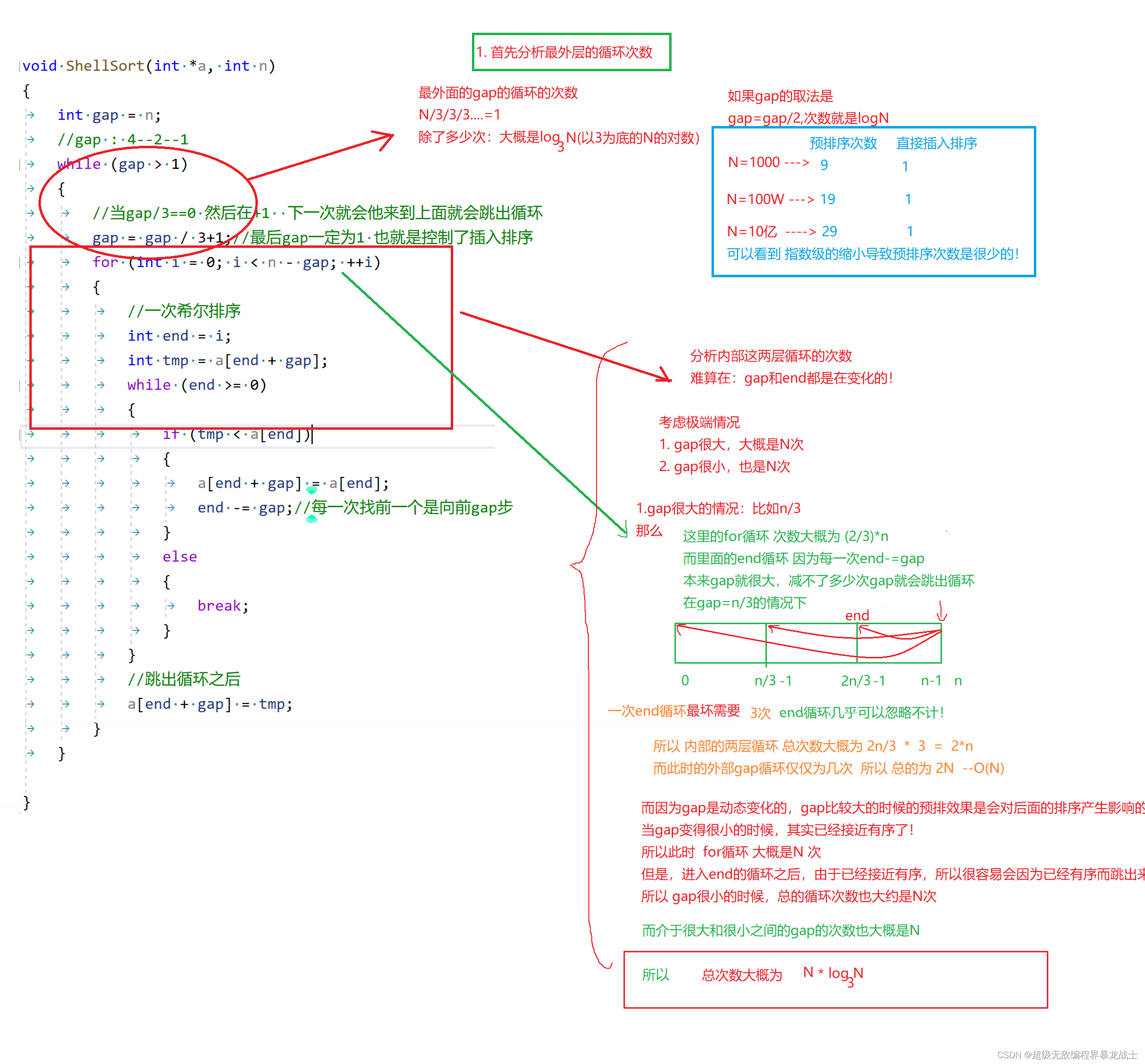
而我们学习了 堆排序–这么高效的排序的时间复杂度才为O(N*logN)
显然希尔排序的效果是毋庸置疑的!
而很多书籍中也给出了一些比较官方的说法
《数据结构(C语言版)》—严蔚敏

《数据结构-用面相对象方法与C++描述》— 殷人昆

综上所述,我们一般取其时间复杂度为 O(N^1.3)








 希尔排序是一种改进的插入排序算法,通过设置间隔gap将数据分组进行预排序,逐步减少gap直到为1,完成排序。文章介绍了希尔排序的思想、图解、gap的选取策略以及C语言实现。预排序通过分组降低数据移动次数,提高效率。时间复杂度通常认为是O(N^1.3),在实际应用中展现出良好的性能。
希尔排序是一种改进的插入排序算法,通过设置间隔gap将数据分组进行预排序,逐步减少gap直到为1,完成排序。文章介绍了希尔排序的思想、图解、gap的选取策略以及C语言实现。预排序通过分组降低数据移动次数,提高效率。时间复杂度通常认为是O(N^1.3),在实际应用中展现出良好的性能。

















 2531
2531

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










