并行与分布式计算导论（四）问题的结构与分解

新的一轮MPI作业已经发布，我尽量在DDL之前给同学们把MPI部分也更新出来！鱼生苦短，争取更咸！

Section 4 问题的结构与分解

OpenMP是我们在C++上进行并行计算的主要库之一。OpenMP是基于内存共享的，适合单机多核、共享内存的系统。所以这里我们关注的是如何将任务做清晰的划分，并交付给一台电脑上的多个处理器进行处理。OpenMP的具体内容将在下一篇文章中讲到，这里首先给出一些OpenMP编程中常常遇到的概念、主要考虑的问题和一些辅助思考的工具。

尽管Foster的设计原则倡导我们要进行四个设计步骤，但实际上OpenMP编程中往往先考虑的是问题的分解和分配问题。分解就是决定哪一部分和哪一部分应该分开，哪一部分先执行哪一部分后执行，哪一部分可以并行，哪一部分只能交给单线程执行；分配就是决定可以并行的任务部分如何分配给不同的处理器，如何权衡并行程度与通讯开销。

问题的分解

同一项工作可以被分解成很多种子任务的组合，不同的分解可能产生多种多样的计算方式和安排方式

并行度（degree of concurrency）

定义：可并行的任务数目

• 在程序执行中可能发生变化

指标：

• 最大并行度：在程序执行过程中，并行任务数的最大值
• 平均并行度：同时并行任务（关于时间的）平均数

并行度与任务粒度（granularity）
（回顾：任务粒度是描述任务划分精细程度的一个指标）

• 两者处于敌对关系，如果任务分的极为细致，那么并行度很高，任务的粒度就很低，如果任务分的笼统，那么粒度很大，并行度却很低
• 既要有一定的并行度，以提高效率，也要保证一定的任务粒度，减少代码工作、增强直观可读性

任务依赖关系图

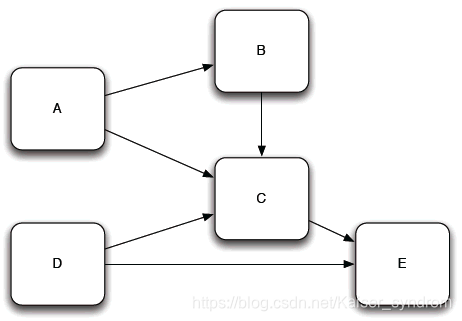
任务依赖关系图（一个有向连通无环图）反映的是任务间的拓扑关系（前后置关系）。一个任务只有等待指向它的所有前置任务都完成才能开始执行

关键路径（重要）

任务依赖关系图中的边展示了任务的拓扑关系

• 关键路径：最长权重的路径
  • ​ 关键路径长度决定了并行程序执行时间的下界

任务交互图（Task Interaction Graph）

注意与任务依赖关系图（Task Dependency Graph）区分，任务交互图展现的是任务间的数据交互关系

• node=task
• edge=interaction or data exchange

并行效果

限制并行效果的因素

• 最小任务粒度（与并行度、任务交互都有