关于PAT Basic Level 1013题的感想

一道神奇的题目

其主要矛盾在于运算

数素数 1013
令Pi表示第i个素数。现任给两个正整数M <= N <= 104，请输出PM到PN的所有素数。
输入格式：
输入在一行中给出M和N，其间以空格分隔。
输出格式：
输出从PM到PN的所有素数，每10个数字占1行，其间以空格分隔，但行末不得有多余空格。
输入样例：
5 27
输出样例：
11 13 17 19 23 29 31 37 41 43
47 53 59 61 67 71 73 79 83 89
97 101 103

• 为什么说他神奇呢，在于这题用python做有天生的缺陷，即运算能力不够。如果直接求前10000个素数，python的运算肯定弱于C/C++，即使逻辑对，判断程序也是直接超时了。

• 除非对python特别优化，运算超过3步的都用全局变量可以到达压缩时间的要求。可是这就背离了我使用python的初衷，python应该是方便快捷优雅的，算法加速交给C去做。

下面给出演示，C++代码来自PAT (Basic Level) Practise （中文）1013. 数素数 (20)
python是自己写

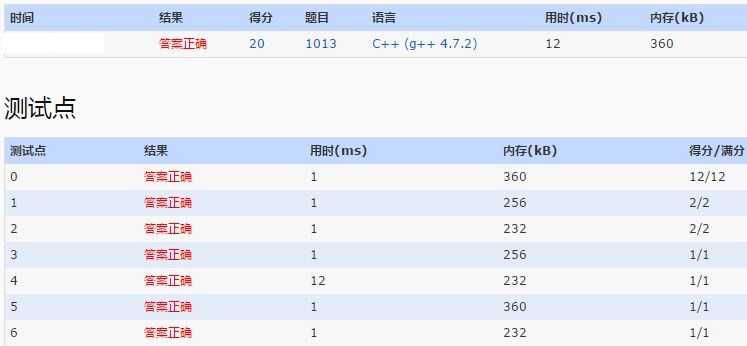
• C++

  • 

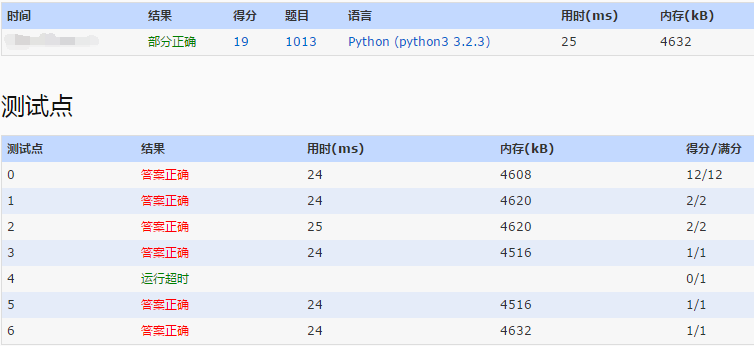
• python

  • 

  • 很明显，两个区别一下出来了。尤其在第4个测试点，C++用了12ms，python本地则使用了2.3s来输出全部前10000个素数。
    顺便把10000个素数给列出来好了该文件在地震中消失

做考试练习时候，简单粗暴是最有效的方法；要是做项目的话，肯定直接混合编程做个C包import example

献上拙劣的Python代码

#coding=utf
#令Pi表示第i个素数。现任给两个正整数M <= N <= 10**4，请输出PM到PN的所有素数。
import math

raw=input()
rawf=raw.split()
n,m=int(rawf[0]),int(rawf[1])
#m=int(rawf[0])
#n=int(rawf[1])
out=""

#判断是否是素数；同时及一个数被所有小于他的数去整除，这里没有优化
def su(n):
  #if prime number
  if n<=1:
    return False
  for x in range(2,int(math.sqrt(n))+1):#迭代器range()替换为素数列表，减少运算
    if n%x==0 :
      return False
  return True

adder=1
#count_su=0
def su_creat():
    global adder
    #global count_su
    while True:        
        adder+=2      
        if su(adder):
            #count_su+=1
            return adder
#素数循环生成器-未来考虑做一个可迭代对象、类

content=[2,]
content.append(su_creat())
while len(content)<max(m,n):
    content.append(su_creat())

#得到前max(m,n)个素数
content=content[min(m,n)-1:max(m,n)]

#print(content)输出对应的格式
for each in content:
    out+=' '+str(each)
    if (content.index(each)+1)%10==0:
        print(out.strip())
        out=''
if len(out)>0:
    print(out.strip())