第一次是在杭电碰到这个题目(1018),当时刚学java的大数,对于阶乘的问题当时都是一股脑的用java去做,而在这里就不行了,或者说没必要用java大数。(用java大数要么打表的时候超内存,要么不打表超时)
题意:1<=n<=10^7,对应一个n输出数n!的位数。
预备知识:
对于一个数n,(log10(n)+1)再取整就是数n的位数。
例如:
log10(1000)=3.000000,log10(1000)+1=4.000000再取整就是4,1000是个4位数。
log10(9999)=3.999957,log10(9999)+1=4.999957再取整也是4,9999是个4位数。
法一(打表法):
//Code:
#include<iostream>
#include<cstdio>
#include<cmath>
const int maxn =10000000;
int a[maxn+5];
int main()
{
//freopen("in.txt","r",stdin);
int t;
double ans=0;
for(int i=1; i<=maxn; i++)
{
ans+=log10(i*1.0);
a[i]=floor(ans)+1;
}
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
printf("%d\n",a[n]);
}
return 0;
}
法二:
斯特灵公式是一条用来取n阶乘近似值的数学公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特灵公式十分好用,而且,即使在n很小的时候,斯特灵公式的取值已经十分准确。 -----引自维基百科
由预备知识可知log10(n!)+1便是答案
但是不能直接带斯特林公式,应该带入log10(n!)化简,不然(n/e)^n会爆炸的。
依据公式把
log10(n!)+1
化成
log10(sqrt(2*acos(-1.0)*n))+n*(log10(n/exp(1.0)))+1
就好了
#include<iostream>
#include<cstdio>
#include<cmath>
int main()
{
//freopen("in.txt","r",stdin);
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
if(n==1){puts("1");continue;}
double ans=log10(sqrt(2*acos(-1.0)*n))+n*(log10(n/exp(1.0)))+1;
printf("%d\n",(int)ans);
}
return 0;
}
注意这个公式对n==1并不成立,所以n==1要特判一下。








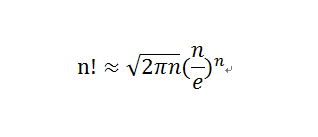














 646
646

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








