论文精讲 | 量子计算二维Isometric张量网络态

于 2023-09-08 15:29:43 发布
阅读量211 收藏
点赞数
文章标签： 量子计算
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Kenji_Shinji/article/details/132761314
版权

内容简介

在模拟量子多体系统时，克服复杂性的指数增长是物理学中一个具有挑战性的目标。目前，对于一维量子系统的基态性质，基于张量网络态（TNS）的方法已经提供了一种有效地方式来给出基本精确的数值解。在二维系统中，通过引入一些算法来优化各种晶格模型的TNS也取得了一些进展。本次，将介绍一种新的量子态的表示方法，即Isometric TNS，该方法可以用于描述二维系统的量子态，并且具有计算上的优势；另外，还将介绍如何利用局部测量来重构MPS的方法，该方法只有线性数量的操作。

相关论文1

标题：Isometric Tensor Network States in Two Dimensions
作者：Michael P. Zaletel and Frank Pollmann
期刊：Phys. Rev. Lett. 124, 037201（2020）

发表日期：2020年1月24日

相关论文2

标题：Efficient quantum state tomography
作者：Marcus Cramer, Martin B. Plenio, Steven T. Flammia, Rolando Somma, David Gross, Stephen D. Bartlett, Olivier Landon-Cardinal, David Poulin & Yi-Kai Liu
期刊：Nature Communications 1, 149（2010）

发表时间：2010年12月21号

01

引言

图片

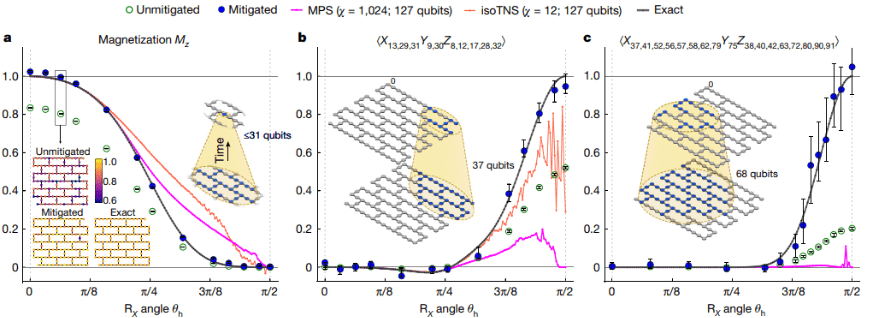
（图片来源：Nature volume 618, pages500–505 (2023)）

最近，IBM实现了在127个量子处理器上进行2维横场Ising模型的模拟，为了进行对比，需要利用经典模拟来求出精确结果。该工作分别用weight-1，weight-10以及weight-17观测量来测量5步trotter的量子电路，得到的实验结果如图。

图片

在为了得到精确解进行经典模拟时，这里采用了Light-cone and depth-reduced（LCDR）的方法。它分为两部分，一部分是通过量子门之间的特性来减少需要模拟的电路层数；另一部分是考虑与观测量A相关的量子比特是局部的，也就是说只需要考虑一部分量子比特的演化就可以计算最终观测量的结果而非全部的127个比特。weight-1,weight-10以及weight-17观测量的相关量子比特数分别为31,37,68。值得注意的是，68个量子比特的模拟仍然超出了经典计算机的暴力模拟的能力。因此，该工作引入了张量网络，1D matrix product states(MPS) 和2D isometric tensor network states(iso TNS), 来进行模拟。

02

矩阵乘积态（MPS）简介

1、张量基础知识

（1）定义与图形表示

图片

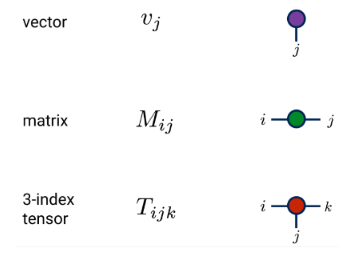
（2）相同指标的收缩

图片

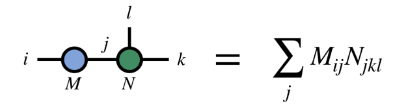
2、MPS

对于一维的有N个格点的系统，若每个格点有d个量子态，则多体态的希尔伯特空间可以表示为格点希尔伯特空间的张量积：

图片

相应任意多体态可以表示为：

图片

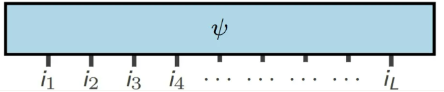
（图片来源：arXir:1603.03039, 2016）

矩阵乘积态(MPS)的核心思想是将多体态表示为:

图片

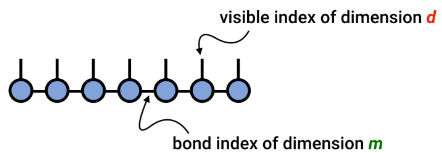
（图片来源：arXir:1603.03039, 2016）

图片

每个单元是一个三阶张量，其中，物理指标是格点量子态， 辅助指标可以看作其与左右系统之间的量子纠缠。

SVD分解：

对于一般

图片

的复矩阵A存在一个分解使

图片

,其中

图片

是一个维度为

图片

的对角矩阵，对角线上的元素被称为奇异值。一般而言奇异值沿对角线按照从大到小的顺序排列。

图片

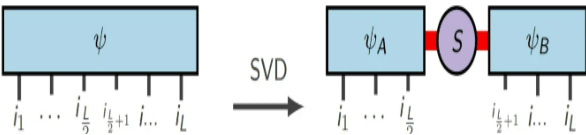
（图片来源：arXir:1603.03039, 2016）

其中S代表奇异值。如果系统两部分之间纠缠不强，奇异值的谱往往衰减很快，只需保留较少的奇异值，就可以保留矩阵大部分的信息。假设我们规定每组施密特分解保留不超过 m个奇异值，最终我们只需要

图片

个实数就能近似表示出这个多体态。相比原本需要

图片

个参数的表示方法，这种表示对于格点数有线性的空间复杂度，效率远远高于原张量积表示指数增长的复杂度。

图片

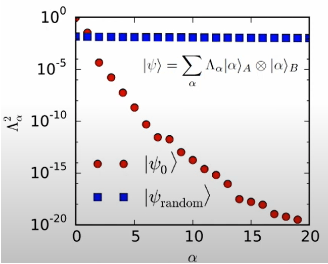
（图片来源：arXir:1603.03039, 2016）

MPS得到的过程：

图片

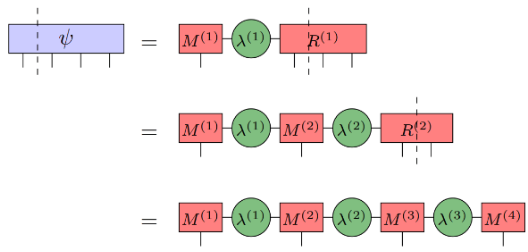
（图片来源：arXir:1603.03039, 2016）

MPO：

对于一个多体算符，像态一样，我们可以将多体算符写为矩阵乘积的形式(MPO)：

图片

和态不同的是，局域算符组成的哈密顿量自然地可以写为矩阵乘积的形式：

图片

图片

（图片来源：arXir:1603.03039, 2016）

矩阵乘积算符作用与矩阵乘积态后仍然保持矩阵乘积结构：

图片

（图片来源：arXir:1603.03039, 2016）

03

Isometric tensor network states in two dimensions

1、摘要

张量网络态是一种很有前途但在数值上具有挑战性的二维量子多体问题的工具。在这篇文章中，作者引入了有isometric限制的TNS ansatz，该形式允许张量网络的高效收缩。为了对ansatz进行数值基准测试，作者首先证明了二维横向场Ising模型基态的MPS表示可以有效地转换为isoTNS，其实，作者实现了一个2D的TEBD算法，并表明它有效地找到了isoTNS形式下二维模型基态的近似值。

2、Isometric张量网络态

1）isometry条件：对于一个

图片

维矩阵M，

图片

或

图片

。张量图示中，一般用箭头表明正交性，规定将张量的内向指标和其共轭张量收缩后得到单位阵。

2）MPS的canonical形式：

图片

其中，A，B满足左右正交条件。左正交条件是指对于前

图片

个量子和自己的转置的缩并是单位阵，右正交条件是指后面的

图片

个量子和自己的转置的缩并是单位阵，

图片

表示一个对角线元素递减的对角阵，也被叫做正交中心。

3) 局部操作的期望值可以直接由

图片

得到，因为其外部的A B张量根据isometry条件收缩为1。

图片

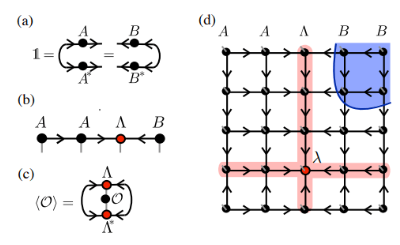
（图片来源：Phys. Rev. Lett. 124, 037201）

4) 推广到二维：

通过类比上式，我们要求TNS的每一行每一列都是isometry，这一约束可以通过进一步要求每个张量是isometry。如上图d所示，红色的部分只有内向箭头，因此，这就是TNS的一维“正交超曲面”，

图片

是标准正交基下的波函数，因此，

图片

可以像MPS一样处理，并且可以将其本身放入一维canonical形式（它的正交中心可以使用一维标准算法自由移动）。对于任意一个算子

图片

，都有

图片

，也就是说，存在一维期望值的降维，该值可以通过标准MPS算法有效地计算而无需进一步近似。这与一般的TNS形成鲜明对比，在一般的TNS中，期望值需要使用整个网络的近似收缩。

3、移动正交超曲面

中心正交形式只有在正交超曲面Lammda可以在整个网络中有效移动时，才对计算有用。在一维中，我们可以通过任意正交矩阵的分解（QR或SVD）来实现正交中心的移动。在二维中，我们同样要实现对

图片

整列的移动。但对于二维系统，正交矩阵分解的方法是失效的，因为它会破坏将

图片

表示为MPS所需要的局部性。

图片

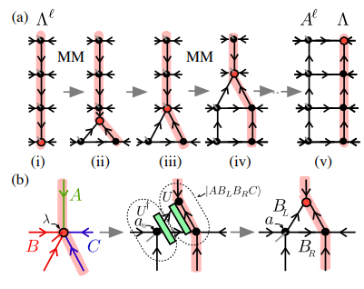
（图片来源：Phys. Rev. Lett. 124, 037201）

在该文章中，作者使用了Moses Move方法来实现对于正交曲面中心的移动。如上图所示，经过MM算法，正交超曲面

图片

分为左正交

图片

和无物理指标的零列状态

图片

的乘积。其中，解压缩是通过连续应用图（b）中所示的“分裂”过程来完成的。中心点

图片

的指标被分组成三态

图片

，并分两步“分裂”成三个张量。

4、MPS 扩展到 isoNTS

图片

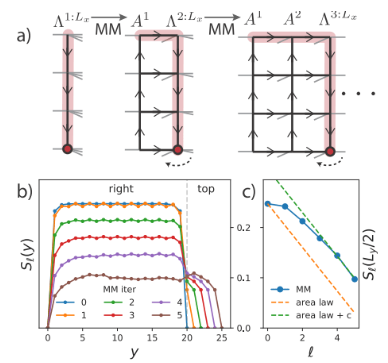
（图片来源：Phys. Rev. Lett. 124, 037201）

给定一个

图片

上的基态波函数

图片

，作者提出了一种迭代算法可以将

图片

放入isoTNS中，并对sing横向场

图片

模型进行了测试。考虑一条

图片

的条带，并使用DMRG获得1D的MPS 

图片

的基态，其中每个“位点”包含相应行的

图片

自旋[图(a)]。如图a中第3个图所示，然后可以使用MM迭代地“分裂”波函数的列

图片

，产生isoTNS。在该例子中，选择bond dimension为6，当g=3.5（顺磁相位)，在每个site误差

图片

为

图片

。在本例中，

图片

。结果如图所示，在图b中展示了沿着正交超曲面进行分割的纠缠熵随着迭代次数的增加而减小。图c说明，对于

图片

，着迭代次数的增加纠缠熵是线性衰减的，符合预期。

5、 

图片

算法

图片

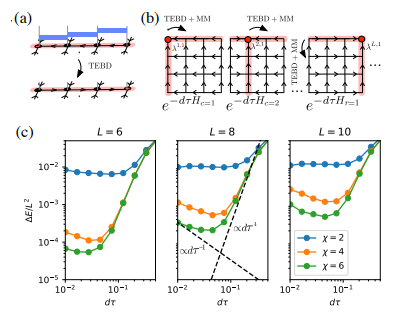
（图片来源：Phys. Rev. Lett. 124, 037201）

作者还实现了

图片

算法，TEBD的主要思路是，利用基于Trotter-Suzuki分解的退火算法，随机初始化的MPS态演化到基态，将该演化过程转换为张量网络收缩问题，并使用TEBD算法求解该收缩。具体来说，对于isoTNS提出了一个Trotterized time stepper，它可以通过虚时演化获得基态。假设只存在最近邻相互作用，我们将哈密顿量拆分为作用于列和行的项

图片

，然后进行Trotterized 

图片

，如图(a)所示。对于1D的TEBD更新，

图片

可以很容易地改进到二阶。我们从正交中心

图片

开始,然后，通过调用标准1D TEBD算法和MM算法逐步的将正交中心移动。在一次扫描中，该算法实际上是两个嵌套的1D TEBD版本，因此称为

图片

。其中，

图片

的演化是通过调用1D TEBD来实现的，其复杂度

图片

，MM的复杂度

图片

，而无约束的PEPS的完整更新复杂度为

图片

。图(c)显示了在不同系统尺寸和最大键维下，g=3.5横场Ising模型的能量误差密度

图片

作为Trotter步长

图片

的函数。随着键尺寸

图片

的增加，最小能量向精确结果收敛。

04

Efficient quantum state tomography

1、摘要

从测量数据中推断量子态对于较大的系统会变得不可行，因为测量的数量和处理它们所需的计算量随着系统规模呈指数级增长。在这篇文章中提出了一种断层扫描方案比系统大小的直接断层扫描更有利。该方法需要对恒定数量的子系统进行统一操作，并且只依赖于线性数量的实验操作。这个方案可以应用于广泛的量子态，特别是MPS。

2、基于酉变换的方案

该方法的该方法的核心思想是找到一个序列操作来从左到右解开一条链的纠缠，这个序列中每个操作都是局部的并且是与维度N无关的。

假设理想状态是

图片

，并且我们假设该量子态是给定bond dimension为R的MPS。该方法的目标是重构这个

图片

。

算法流程：

图片

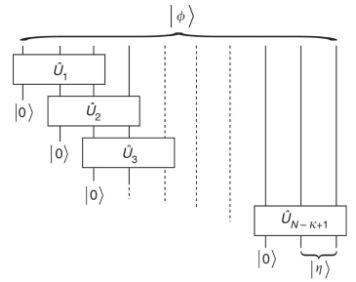
（图片来源：Nature Communications 1, 149（2010））

1)、首先我们取

图片

，然后对前k个sites做标准的量子态层析，则前k个sites的约化密度矩阵为：

图片

，这个约化密度矩阵有特征分解

图片

，其中，

图片

。因此，存在一个少一个qudit的密度矩阵，它的rank R和特征值

图片

和

图片

相同。

2)、接着，我们进一步利用

图片

的信息来针对前k个位置构造一个酉矩阵

图片

，这个

图片

可以对第一个site进行解纠缠 

图片

3)、将

图片

作用到原来的态上就可以得到:

图片

其中，

图片

是一些在

图片

位置上的纯态。


4)、然后对接下来的第2到k+1个位置重复上述的过程。以此类推，我们就可以得到一个酉矩阵的序列

图片

，其中每个

图片

作用在

图片

个位置。这个序列使得

图片

变为

图片

，其中每个

图片

作用在

图片

个位置。这个序列使得

图片

变为

图片

，其中,

图片

是一些在最后k-1个位置上的纯态。

综上所述，该方案推导了用于制备MPS的量子电路。通过

图片

和

图片

可以很容易地得到MPS分解。

3、误差
该方法的误差主要来源于两个方面，一是由于bond dimension的限制导致不能完全表达这个量子态，二是来由于测量带来的误差。

给定一个估计的解纠缠的酉矩阵

图片

，任意态

图片

可以被表示为：

图片

，其中，

图片

是误差向量。

在接下来的步骤中，我们可以得到如下形式的态：

图片

，其中，

图片

是累计误差。

我们可以通过测量标准基中的前i个粒子并在全零的结果上进行后选择来截断该误差向量。这种情况发生的概率大致为

图片

，并使系统处于状态

图片

。

经过一系列的酉变换得到的最终的状态为：

图片

其中，

图片

，因此，

图片

。

我们可以发现误差随着粒子数量线性累计，将我们得到的MPS记为：

图片

，则我们有：

图片

其中，

图片

。总体误差最多是每一步中单个误差的总和。

昇思MindSpore
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
张量网络 part 1
07-03
Modern applications in engineering and data science are increasingly based on multidimensional data of exceedingly high volume, variety, and structural richness. However, standard machine learning algo- rithms typically scale exponentially with data volume and complex- ity of cross-modal couplings - the so called curse of dimensionality - which is prohibitive to the analysis of large-scale, multi-modal and multi-relational datasets. Given that such data are often efficiently represented as multiway arrays or tensors, it is therefore timely and valuable for the multidisciplinary machine learning and data analytic communities to review low-rank tensor decompositions and tensor net- works as emerging tools for dimensionality reduction and large scale optimization problems. Our particular emphasis is on elucidating that, by virtue of the underlying low-rank approximations, tensor networks have the ability to alleviate the curse of dimensionality in a number of applied areas. In Part 1 of this monograph we provide innovative solutions to low-rank tensor network decompositions and easy to in- terpret graphical representations of the mathematical operations on tensor networks. Such a conceptual insight allows for seamless migra- tion of ideas from the flat-view matrices to tensor network operations and vice versa, and provides a platform for further developments, prac- tical applications, and non-Euclidean extensions. It also permits the introduction of various tensor network operations without an explicit notion of mathematical expressions, which may be beneficial for many research communities that do not directly rely on multilinear algebra. Our focus is on the Tucker and tensor train (TT) decompositions and their extensions, and on demonstrating the ability of tensor networks to provide linearly or even super-linearly (e.g., logarithmically) scalable solutions, as illustrated in detail in Part 2 of this monograph.
张量网络
芦金宇的专栏
06-21 4543
简单地介绍一下张量网络是什么，以及它有什么应用。1. 张量（tensor）张量网络中的张量，和微分几何和GR中的张量场并不完全相同。在微分几何中，一点处的张量是基于流形上该点的切空间的。一个(m,n)型张量是指将m个协变矢量（余切矢量，cotangent vector）和n个逆变矢量（切矢量，tangent vector）映射到数域上的多重线性映射。取定一组基，这个多重线性映射可以用一系列分量表示...
张量网络(1)
fgh123的博客
06-30 1358
张量积定义 Mdd,NddM_{dd},N_{dd}Mdd​,Ndd​ d2×d2d^2\times d^2d2×d2 M⊗N=(m11Nm12N⋯m1dNm21Nm22N⋯m2dN⋮⋮⋱⋮md1Nmd2N⋯mddN) M\otimes N= \left( \begin{array}{cccc} m_{11}N&m_{12}N&\cdots&...
张量网络算法基础（九、张量网络机器学习【下】）
qq_45801570的博客
08-31 771
张量网络图片生成与压缩一、监督/非监督张量网络机器学习二、张量网络图片生成与压缩三、监督性张量网络机器学习 一、监督/非监督张量网络机器学习 ∣ψ⟩\left| \psi \right\rangle∣ψ⟩ 是一个L-qubit的量子态，它的参数复杂度会随着特征个数L呈指数上升，张量网络机器学习的中心思想之一就是将∣ψ⟩\left| \psi \right\rangle∣ψ⟩用张量网络表示，从而使参数复杂度降低到多项式级。 在给定N个训练样本{X[n]}\left\{ {{X}^{[n]}} \right
2d-isometric:二维等距测试的游乐场
03-16
在IT行业中，2D等距（2D Isometric）是一种常见的图形表示技术，它用于创建具有立体感的二维图像。这种技术广泛应用于游戏开发、地图绘制、数据可视化等领域，因为它可以提供一种直观的方式来展示三维空间中的对象，...
Isometric-engine.rar_isometric
09-14
斜视角图形引擎的设计 这是讲述斜视角图形引擎的设计原理 目录 1.视角的选择和坐标变换 2.地表的数据组织及滚屏 3.动态地表的实现 4.物体的绘制及遮挡运算 5.复杂的精灵控制 6.让场景更生动 7.深入了解物体精灵 ...
hacky_isometric
02-04
在IT行业中，"hacky_isometric"这个标题可能是指一个项目或者工具，它与等轴测（isometric）图形和晶体（Crystal）计算机图形学有关。等轴测是一种图形绘制技术，常用于创建2D视图，表现出3D物体的立体感。这种技术...
Isometric Pack 3d v1.01.unitypackage
01-31
unity 方块包
Unity-Isometric-Jump-Movement-Controller-master.zip
09-01
等距视角（Isometric Perspective）是一种伪三维视角，它不使用标准的透视图，而是将图形以45度角投影到平面上，使物体的前后、左右和上下的比例相同，创造出类似3D的效果，同时保留2D的平面布局。在Unity中，等距...
张量网络 降维算法 大规模优化
07-03
Part 2 of this monograph builds on the introduction to tensor net- works and their operations presented in Part 1. It focuses on tensor network models for super-compressed higher-order representation of data/parameters and related cost functions, while providing an outline of their applications in machine learning and data analytics. A particular emphasis is on the tensor train (TT) and Hierarchical Tucker (HT) decompositions, and their physically meaningful interpre- tations which reflect the scalability of the tensor network approach. Through a graphical approach, we also elucidate how, by virtue of the underlying low-rank tensor approximations and sophisticated con- tractions of core tensors, tensor networks have the ability to perform distributed computations on otherwise prohibitively large volumes of data/parameters, thereby alleviating or even eliminating the curse of dimensionality. The usefulness of this concept is illustrated over a number of applied areas, including generalized regression and classification (support ten- sor machines, canonical correlation analysis, higher order partial least squares), generalized eigenvalue decomposition, Riemannian optimiza- tion, and in the optimization of deep neural networks. Part 1 and Part 2 of this work can be used either as stand-alone separate texts, or indeed as a conjoint comprehensive review of the exciting field of low-rank tensor networks and tensor decompositions.
论文研究-时域电磁计算统一解决方案研究 .pdf
08-25
时域电磁计算统一解决方案研究，吴先良，黄志祥，构造了时域Maxwell方程的Hamilton函数，利用函数变分，得到了对应的Hamilton正则方程，将时域电磁问题的数值计算转化为Hamilton系统正则方��
张量网络算法基础（八、张量网络机器学习【上】）
qq_45801570的博客
08-31 1936
张量网络机器学习一、 机器学习基本思想二、希尔伯特空间、特征映射与量子概率三、等概率先验假设与量子懒惰学习 一、 机器学习基本思想 机器学习模型可以看作是一个黑盒子，接受输入信息之后，信息接受一系列的操作输出目标信息。从数学的角度来讲，机器学习可以看作是数学映射fff，映射的变量就是输入信息xxx，且包含变分参数www，输出信息yyy为目标信息，形式上可写成y=f(x;w)y=f(x;w)y=f(x;w)。 举几个生活中常见的例子：在自动驾驶中，输入驾驶环境信息及交通规则等，输出驾驶操作动作；在图形识别中
张量网络编程学习笔记（4-1）：QRNN原理入门，QRNN_predic_time_series 的简介
最新发布
weixin_47134520的博客
07-23 570
（1）前文提到的ADQC ~ FCNN：一种量子意义上的前馈层（2）循环结构QRNN = ADQC + 循环迭代：一种量子意义上的时序预测组合。
张量网络与机器学习
abcxyz11111的博客
04-17 685
这一章我们主要讲讲如何使用张量网络来做机器学习，里面有些比较细节的东西后续会通过链接贴上来。 基本思想 以图像处理为例，我们是将每张图片映射成希尔伯特空间中的向量，图像像素的所有可能构型对应着子空间的基矢，纯态在基矢上的投影对于构型的概率幅。图像生成的过程就像是量子态坍缩的过程。 特征映射 这里是讲如何将经典的图片元素映射成qubit的直积。注意一下这里的第二步，子空间维度被设定为了2（降低计算复杂性），但是像素本身的维度D>2，所以我们单考虑一个子空间，不同像素之间的内积不等于0。考虑到整个图片对
张量网络系列（一 从张量到张量网络）
欢迎来到 豪哥 的博客
07-22 6710
历时半个多月，我们终于从刚开始的张量学习 ，到现在的张量网络，本人真的是一路艰辛，哎 ，打油诗一首表心意： 本是计科专业狗，年少无知四顾首。 无赖量子吸引我，前路茫茫无处走。 早知人生本就难，科研门前抖一抖。 陷入深渊尚未知，乐此不疲直挥手。 半路出家尝滋味，心理防线已失守。 老板教诲不敢忘，硬着头皮往前走。 其中滋味难传达，卿知否？卿知否？ 前路迢迢虽泥泞，组内都是好盆友。 光阴不可再虚度，忆往事痛心疾首！ 下定决心埋头干，吾定要大显身手！ 祖国崛起志士缺，天下英雄谁敌手？ 夜半三更睡不着，写首诗精神抖擞
3-1 张量网络入门 Tensor Network learning
ZhongYun的博客
05-30 386
张量网络定义 首先，从我们熟知的向量和矩阵来引入张量：从形式上看，它们都是数组。向量是一维数组，矩阵是二维数组，张量即为高维数组。
十二、张量网络机器学习（一）
上官永石的博客
08-30 1009
十二、张量网络机器学习 1. 机器学习基本思想        简单来说，机器学习可以看成是一个接受输入信息后，输出想要得到的目标信息的一种模型。我们进行机器学习的目的就是找到这种模型，让这种模型能够进行这种信息 的转换。        机器学习的几个常见的例子如下： 图形识别中，输入图片信息，输出图像分类 语言翻译中，输入源语言文字，输出翻译后语言文字 自动驾驶
张量网络论文学习1——张量网络的背景和意义
Peace__mind的博客
04-24 878
目录系列背景简介张量网络的背景量子多体系统的问题张量网络方法的意义 系列背景简介 我算是非常偶然接触到这个领域的，因为虽然作为物理系的学生，但却一直想着去搞计算机，对于物理专业来说，除了本科要学的四大力学，以及大略知道什么固体物理，原分光冷原子之类的一系列名词，就没有更多的了解了。很快就要分流了，才发现自己实际上对于物理的方向还很不了解，才发现物理的方向多种多样，内容也丰富多彩。张量网络恰好是我学...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值