MindSpore AI科学计算系列 | PDEformer——基于昇思MindSpore的偏微分方程基础模型研究与实践

本文链接：https://blog.csdn.net/Kenji_Shinji/article/details/139462940

近日，华为AI4Sci Lab联合北京大学董彬教授基于昇思MindSpore框架提出PDEformer-1[1]模型，并于昇思人工智能框架峰会2024上正式发布。这是一种可以直接输入任意PDE形式的神经算子模型，通过生成PDE计算图、编码图数据、解码求解的技术路线以达到快速、精准求解大多数一维PDE的目的。PDEformer-1经过在大规模一维PDE数据上进行的预训练，在训练数据分布内Zero-shot预测精度高于针对某一种方程专门进行训练的专家模型(如FNO[2]、DeepONet[3])。针对训练集以外的数据分布，PDEformer-1还表现出了出色的小样本学习(few-shot learning)能力，能通过少量的样本迅速泛化到新的下游任务。与此同时，PDEformer-1还可以作为正问题算子的代理模型直接运用到反问题中。下文将展开介绍该模型的具体信息及内容。

背景

偏微分方程(PDE)与众多物理现象及工程应用紧密相连，涵盖机翼设计、电磁场模拟、应力分析等广泛领域。在这些实际应用中，PDE的求解往往需要反复进行。尽管传统的PDE求解方法以其高精确度著称，但它们在计算资源和时间上的消耗较大，且难以适应各种PDE形式的统一求解。近年来，随着深度学习的发展，领域中提出了许多种基于深度学习方法的PDE求解器，其中的许多方法相比传统求解器有明显的速度优势，因而受到了很多关注。鉴于通用AI模型在计算机视觉与自然语言处理领域大放异彩，华为AI4Sci Lab携手北京大学董彬教授，开创性地构建了一个针对偏微分方程数值求解的通用模型。这一模型旨在实现用一个统一框架对不同PDE进行数值求解，从而大幅提升求解效率。任意给定的PDE均能通过该通用模型直接求解，无需针对不同方程进行定制化的模型设计。与只能在特定数据集上训练的专家模型(如FNO、DeepONet)相比，该通用模型得益于对不同PDE的大量训练，展现出更高的求解精度，并具备快速泛化到其他方程的能力。

PDE数值求解领域当前可分为传统的数值求解方法与AI求解方法两大类别。传统的求解PDE方法，如有限差分方法(FDM)和有限元方法(FEM)等，在处理问题时通常会将求解区域划分为网格，然后利用不同的函数空间去逼近解空间，从而将PDE的数值求解转化为线性方程组的求解。这一过程中，往往需要处理大型的线性系统，因此在求解阶段会消耗大量的计算资源和时间。近年来，随着神经网络和相关软硬件的飞速进步，AI求解器得到了显著的发展。这类求解方法以已知的数据或方程原理为基础，通过对神经网络的训练，得到PDE的数值解，其技术路径主要可以划分为三类。

第一类 AI 求解方法是单个PDE求解方法。它利用神经网络直接表示方程解，从而避开了求解区域的网格离散化过程。这类方法主要依赖于PDE的固有形式及其边界条件来进行求解，物理信息神经网络(PINN[4])便是其中的典型代表。该方法无需依赖传统求解器生成训练数据，因此展现出了极高的灵活性。然而，其求解过程需要消耗大量计算资源，且每遇到不同形式的PDE或参数变化时，都需要重新训练模型，这在一定程度上限制了其快速求解的能力。第二类方法是参数化PDE求解方法。它借助传统求解器生成特定方程的大规模数据集，并通过神经网络建立从PDE参数到解的映射关系，如FNO和DeepONet等便是这类方法的杰出代表。这类方法一旦完成训练，对于同类方程和相似参数的推理时间将大大缩短。然而，面对复杂多变的实际场景，每种不同的PDE都需要训练一个专门的专家模型，这使得通用性成为一大挑战。第三类方法则致力于构建一个能够求解多类PDE的通用模型。借助语言模型的发展，研究者们开始尝试将语言模型与传统模型相结合，以构建能够处理多类PDE的基础模型，如PITT[5]、PROSE[6]等研究工作便是这一方向上的积极探索。尽管这种方法在理论上具有广泛的适用性，但在实际操作中，如何将显式的PDE表达与数据有效融合仍然是一个亟待解决的问题。当前的编码方式显得不够自然，且当处理更多、更复杂的PDE时，可能会面临更大的挑战。因此，这类方法仍有待进一步的改进和优化，以实现更广泛、更高效的应用。

华为AI4Sci Lab与北京大学的董彬教授携手，基于昇思MindSpore框架共同提出了PDEformer-1模型，这是一种创新的数据驱动方法。PDEformer-1的核心在于将不同PDE的符号信息，即方程的形式，转换为多样化的计算图表示形式，其中图中的节点代表未知场分量、标量系数以及微分或代数运算等关键要素，而边则体现了这些要素间的逻辑关系。此外，模型为每个节点分配了高维特征输入，以捕捉相关的数值信息，包含初值条件、方程有关系数等。然后模型采用Graph Transformer(如 Graphormer[7])来整合图中的符号和数值信息，并针对每个待解的场分量产生一个表征其解的隐式编码。最后模型使用隐式神经表示(INR)方案来描述方程各分量的解，根据所得到的隐式编码来预测特定时空坐标上的解分量值。通过对广泛多样的一维PDE数据进行大规模的预训练，PDEformer-1在 Zero-shot预测任务中表现出卓越的性能，超越了那些仅针对单一方程类型训练的专家模型(如 FNO、DeepONet)的精度。对于训练集分布外的场景，PDEformer-1也证明了其出色的小样本学习能力，能够利用有限的新数据迅速适应新的下游任务。此外，PDEformer-1还能直接应用于反问题的求解，例如，它可以作为正问题算子的代理模型，用于常数系数反演、源项反演、波方程速度场反演。

1、技术路径

PDEformer-1考虑定义在(t, x)∈[0, 1]×[-1, 1]上的一维含时偏微分方程，其一般形式为：

其中，c_1, c_2, …∈R是实值系数，s_1(x), s_2(x)…是标量函数(在方程中可作为初始条件、系数场等)，u_1, u_2…为待求解的物理场的各个分量。在这里，微分或边界条件算子F具有符号表达式，其中可能涉及微分和代数运算。PDEformer-1的目标是构建一个方程解的代理模型，形式为：

它将PDE的符号形式F及其中涉及的数值信息c_1, c_2, …, s_1(x), s_2(x),…作为输入，输出相应方程的预测解u_1, u_2…。

图1周期边界条件对流方程(单分量)求解流程

图 1 以具有周期边界条件的对流方程(单分量)为例。在求解PDE的过程中，PDEformer-1先将方程形式表示为一个计算图，接下来应用Graph Transformer ，将PDE有关的数值信息进行编码，最后将编码结果输入一个INR ，从而得到PDE在特定时间-空间坐标下的解。

1.1 构建PDE计算图

PDEformer-1 的第一步是将F(关于待求解 PDE 形式的符号信息)表示为计算图。在这个计算图中，一个节点可以代表一个未知场分量(用 ‘UF’ 表示)、标量系数(‘SC’)、系数场(‘CF’)、初始条件(‘IC’)，以及微分或代数运算，一条有向边则用于指定参与运算的操作数。这构成了一个具有异构节点和同构边的有向无环图(DAG)。

然后，为了体现PDE中涉及的数值信息，图中的每个节点被赋予一个d_e维的输入特征。对于一个标量系数c，它的数值将被输入一个标量编码器(scalar encoder)，编码器给出的d_e维的输出将作为相应‘SC’节点的输入特征。考虑到标量函数 s(x) 包含信息的丰富性，我们引入了N个新的“分支”节点与每个这样的标量函数进行链接，类型为:b_1, b_2,…,b_N。用这N个节点的输入特征表示 s(x) 所包含的数值信息。具体地说，PDEformer-1 采用函数编码器(function encoder)，其输入为一系列散点{(x_i, s(x_i))}(散点的位置与分布可任意选取)，输出为d_e*N维向量。这个向量被用于给出N个分支节点的输入特征μ_j^l。图中的这些分支节点与s(x)所对应的‘IC’或‘CF’节点之间有相连的边。所有剩余节点的输入特征都被设为零(为简化编程实现，实际上是标量编码器接收零输入时的对应输出)。

此外，每个待求解的场分量连接了L个额外节点，类型为：m_1, m_2,…,m_L，并与相应的‘UF’节点连接起来。后续使用graph Transformer处理图数据时，PDEformer-1将关于这一场分量的预测解的信息汇总到这些新节点所对应的嵌入向量当中。

1.2 编码图数据

上一步获得的图数据包含了PDE涉及的符号与数值信息。在图数据处理阶段，Graph Transformer将融合这些信息，并为每个待求解的场分量u_j生成一个表征解的隐编码：

Graph Transformer，是一类功能强大的、基于Transformer的图神经网络，擅长捕捉和表达复杂的图结构信息。Graph Transformer输出层中类型为m_l(且与 u_j 对应)节点对应的嵌入向量记为μ_j^l∈R^{d_e}。它将在下一步中参与“调制”INR中的第l个隐藏层，以生成最终的预测解。

1.3 解码获得PDE预测解

PDEformer-1 采用 INR(隐式神经表示)方式来表示方程解的各个分量。这一网络以时空坐标 (t,x)作为输入，并根据隐编码μ_j来预测出相应的方程解分量在该坐标点的取值uhat_j(t, x)。通过这种方式给出的预测不依赖于特定的离散网格。在具体实现时，PDEformer-1选用了Poly-INR架构，并做了相应的适配(见下图)。Poly-INR的隐层数目为L，其中第l个隐层的激活值将被μ_j^l “调制”。注意PDE中的所有的分量共享同一套INR的参数，它们仅仅是对应的隐编码μ_j有所不同。

图2 INR结构示意图

2、实验结果

PDEformer-1通过精心构建一个包含丰富多样PDE形式的自定义数据集，为模型的预训练提供了坚实的基础。经过预训练后，PDEformer-1在PDEBench[8] 数据集上展现出了出色的Zero-shot推理能力，充分展示了其出色的泛化性能。为了进一步提升推理性能，我们对PDEformer-1进行了微调，并在PDEBench上取得了显著的精度提升。此外，在波方程数据集上的微调和推理过程中，PDEformer-1展现出了对未知算子的强大适应性，证明了其在实际应用中的灵活性和实用性。更令人振奋的是，PDEformer-1不仅适用于正问题的求解，还被成功扩展到了反问题的求解中，包含常数系数反演、源项反演、波方程速度场反演等复杂任务。

2.1 预训练

预训练数据集包含了如下形式的方程的解：

其中，f_i(u)=c_{i1}u+c_{i2}u^2+c_{i3}u^3, i=0, 1，每个系数c_{ik}以概率0.5被设为0，其他情况下从U([-3, 3])中随机抽取。系数场s(x), κ(x)以一定概率取为不依赖空间的常数或0，其中κ(x)取值范围为[10^{-3}, 1]。初始条件g(x)与非常数源项s(x)与PDEBench数据集的初始条件生成方式相同。对于非周期边界情形，边界条件种类从Dirichlet、Neumann和Robin中随机选取，齐次与否也随机选取，且左右两端点的边界条件独立生成。

我们使用开源Python包Dedalus V3生成训练数据集的数值解，若Dedalus不能生成PDE的最终解，或者生成的解L_∞>10，这样的数据会被丢弃，不记录在数据集中。

在预训练过程中，PDEformer-1在训练数据集上的相对误差为0.0084，而在测试数据集的相对误差为0.0133。下图展示了预训练后的PDEformer-1在测试数据集上的预测结果，该模型在不同PDE问题的求解上均展现出了高度的准确性。

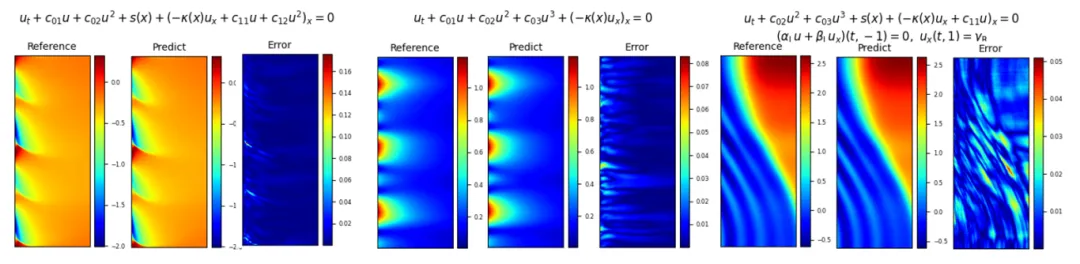
图3 PDEformer-1 在训练数据集中的部分样本上的推理效果(横轴为时间分量，纵轴为空间分量)

可以看出，在与预训练集设定相同的数据集上，PDEformer-1能够达到出色的求解效果。

2.2 正问题

1）PDEBench数据集相关正问题求解

PDEBench提供了一个基于偏微分方程(PDEs)的数据集，旨在评估机器学习模型的求解性能。这一数据集具有独特的特点：包括从常见案例到更具挑战性和现实问题的更广泛范围的PDEs，它比以往工作中的数据集大得多，包含Burgers、Advection和Reaction-Diffusion方程。 PDEformer-1团队对模型在该数据集上的表现进行了多样的评估，以证明PDEformer-1的通用性。

我们的测试包含Burgers 中υ=0.1，υ=0.01以及Advection方程β=0.1的情况(这些情况包含在训练集内)，以及Burgers中υ=0.001，Advection方程中β=1的情况，Reaction-Diffusion方程中υ=1，ρ=1的情况，这些情况并不包含在训练集内(Out-of-Distribution，OOD)。PDEformer-1在上述数据集上进行了Zero-shot推理，与此同时还进行了微调实验(其结果对应下表中的PDEformer-1 (Finetune) )，这些结果与U-Net，FNO和DeepONet等常见Baseline相比有明显的优势。在下图(左)中，PDEformer-1在Zero-shot预测任务中表现出卓越的性能，超越了专家模型的精度。下图(右)中展示了PDEformer-1直接推理(Zero-Shot)的结果以及微调(Finetune)的结果。对于训练集中没有的系数分布，PDEformer-1展现了出色的适应能力，微调的结果超过了专家模型。

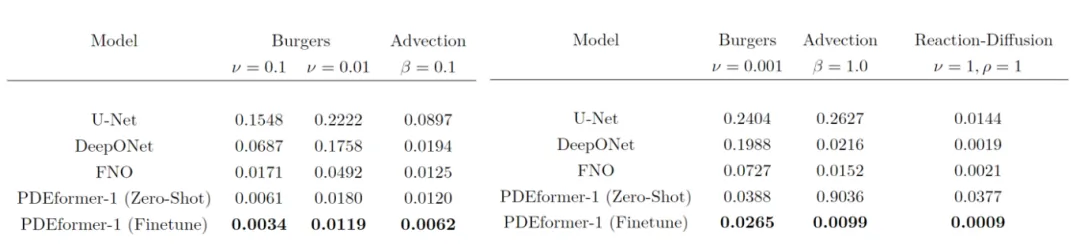
图4 系数In-Distribution(左)、系数 Out-of-Distribution(右)

为了比较微调PDEformer-1和训练传统神经算子的效率，我们对Advection 方程(β=1，训练集不包含这样的系数)在100个样本上微调，并进行了比较分析。如图3所示，PDEformer-1 在大约仅100次迭代中迅速达到较高的精度。相反，从零开始训练的FNO模型需要几千次迭代才能达到较高的精度，并且结果的测试误差更高。这种对比突显了 PDEformer-1的快速适应以及精确求解的能力，标志着相比于专家模型的显著进步。

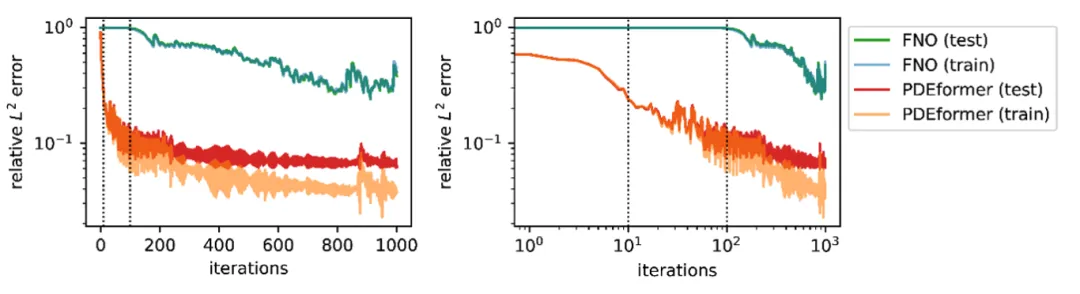
图 5 微调速度对比

我们还从推理速度的角度将PDEformer-1与专家模型及传统数值解法进行了比较，结果如下图所示。PDEformer-1与传统数值解法相比，具有量级上的优势，而与机器学习中的专家模型相比，并没有特别显著的差距。

图6 PDEformer-1 与其他求解器推理速度对比

2）波方程正问题求解

波方程包含时间二阶导算子，其计算图中会出现两个相互连接的dt节点(如下图所示)：

图 7 波方程计算图

这一元素在预训练数据集中并未出现。为检验模型对于新算子的适应能力，我们对PDEformer-1在波方程数据集上进行了微调。数据集对应的方程形式如下：

其中，Lu=-c(x)^2u_{xx}, -c(x)(c(x)u_x)_x, -(c_2(x)u_x)_x中随机选取，f(u)=c_au+c_2u^2+c_3u^3, c_k~U([-3, 3])，并以0.5的概率被设置为0。该数据集包含周期边界以及非周期边界各 200k 条，其中非周期边界在两端点分别独立地从Dirichlet、Neumann、Robin、Mur型边界条件中随机选取一个。在微调过后，PDEformer-1在波方程数据集上的nRMSE达到了：0.051(周期)，0.046(非周期)。

2.3 反问题

为了验证 PDEformer-1在下游任务中的应用潜力，我们将PDEformer-1作为正问题算子的代理模型应用到反问题中，并观察其结果。

1)反问题形式1：常数系数反演

该反问题是在已知方程形式和带噪声的初值条件下，根据在固定位置、时间的观测(带噪声)，来恢复方程中的未知系数。例如，已知方程形式为u_t+c_11u+c_12u^2+(-κu_x)_x=0，根据观测到的信息以及初始条件来恢复目标参数c_11, c_12, κ。对于每个PDE，我们假设能够获取8个不同的初始条件下的解，可观测到的样本点局限于8个固定的空间位置，并且各位置上能够产生观测的点也是随机的(平均每个空间位置能产生8个观测样本)。这些点的观测值上会添加相对幅度为10%的噪声，而作为PDEformer-1输入的初值上也会添加3%的噪声。由于恢复系数问题的损失函数高度非凸，我们使用粒子群优化(Particle Swarm Optimization，PSO)方法来求解相应的优化问题。

下图展示了 PDEformer-1 结合PSO算法达到的出色反演效果。其中，左侧三幅图分别为真实数据、噪声数据、观测到的数据，右侧为真实系数及恢复值的情况。我们用散点绘出求解结果，可以看出，恢复的系数与真实值非常接近，散点主要分布在y=x线上。一些异常值的存在可以归因于这个反问题本质上的病态性。

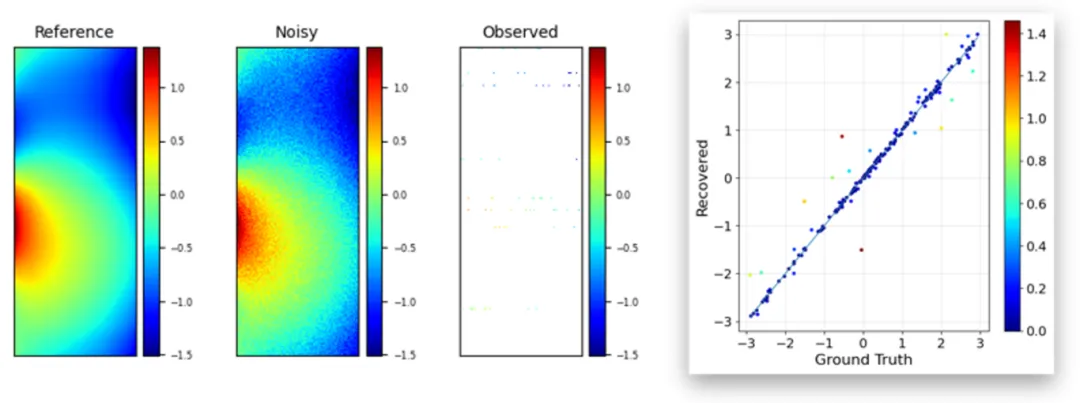
图8 Noise 为10%的系数恢复情况

如上图可知，在噪声较大的情况下，嵌入 PDEformer-1 的反问题求解仍能较好地恢复参数的值。

2)反问题形式2：源项反演

该反问题是在已知方程形式和带噪声的初值条件下，根据在固定位置、时间的观测(带噪声)，来恢复方程中的未知源项场。

在这个任务中，我们所采用的方程形式分布仍与预训练数据集相同，而需要恢复的对象是其中对应于方程源项的系数场s(x)。对于每个PDE，我们假设能够获取100个不同的初始条件下的解，可观测到的样本点局限于32个固定的空间位置，平均每个空间位置能获取32个观测样本。这些点的观测值上会添加相对幅度为1%的噪声，而作为PDEformer-1输入的初值上添加3%的噪声。相应的优化问题使用梯度下降算法求解。下图展示了 PDEformer-1 在反问题中的应用，我们用红色曲线代表恢复结果，蓝色曲线代表真实值，对于三个不同的测试样例，两个图像之间均未见明显偏差，反演的精度较高。

图9 源项(系数场)恢复结果

3）反问题形式3：波方程速度场反演

在波方程数据上对PDEformer-1进行了增量训练以后，为了进一步探究微调后的 PDEformer-1在反问题上的求解能力，我们用它来恢复波方程中的未知速度场c(x)。波方程的形式为Eq. 5。其中，Lu=-c(x)^2u_{xx}, -c(x)(c(x)u_x)_x, -(c_2(x)u_x)_x随机选取。对于每个方程，我们假设能够获取32个不同的初始条件下的解，可观测到的样本点局限于32个固定的空间位置，平均每个空间位置能获取32个观测样本。这些点的观测值以及作为PDEformer-1输入的初值均会添加一定幅度的噪声。下图展示了 PDEformer-1在不同噪声环境下反问题中的应用(我们用红色曲线代表恢复结果，蓝色曲线代表真实值)。

图10 不同噪声情况下的波速场恢复结果

在不同的噪声环境下，PDEformer-1得出的反演结果均与真实值没有太大偏差，达到了较高的精度。

3、总结及展望

目前版本的PDEformer-1通过将PDE表达为计算图的方式求解一维含时PDE，可以同时求解不同形式的方程，在多个测试集上表现出了高于专家模型的求解精度。对于系数OOD或方程形式OOD(波方程)的情况，也能够基于预训练模型进行快速的增量训练，无需从零开始。在处理下游任务如反问题求解时，PDEformer-1也表现出良好的适应性，能够在多种问题设置中提供准确的解决方案。然而，需要承认的是，现阶段的PDEformer-1模型只针对一维含时方程进行了训练，主要作为概念验证，它的实用价值仍比较有限。就科学研究、工程、医疗等领域的实际问题而言，其中所关注的PDE主要集中在二维、三维甚至更高维度的方程。为了未来能够将 PDEformer-1运用到这些真实场景当中，团队将探索如何高效地训练PDEformer-1 ，使其能够求解二维、三维的方程，以及不同维数的方程数据如何同时参与训练。所考察的方程类型范围也将进一步拓宽，其中可能涉及更复杂的函数、代数、微分与积分运算，并且也会针对二维与三维PDE可能涉及的复杂区域形状探索相应的处理方式。此外，团队也会考察更多种类的下游任务。除了已经做了初步探索的反问题以外，未来 PDEformer-1 还会被应用到优化设计、控制、不确定性量化等更广泛的任务类型当中。

参考文献

[1] Z. Ye, X. Huang, L. Chen, H. Liu, Z. Wang, and B. Dong, “PDEformer: Towards a Foundation Model for One-Dimensional Partial Differential Equations.” arXiv, Feb. 19, 2024. doi: 10.48550/arXiv.2402.12652.

[2] Z. Li et al., “Fourier Neural Operator for Parametric Partial Differential Equations.” arXiv, May 16, 2021. doi: 10.48550/arXiv.2010.08895.

[3] L. Lu, P. Jin, and G. E. Karniadakis, “DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators,” Nat Mach Intell, vol. 3, no. 3, pp. 218–229, Mar. 2021, doi: 10.1038/s42256-021-00302-5.

[4] M. Raissi, P. Perdikaris, and G. E. Karniadakis, “Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations,” Journal of Computational Physics, vol. 378, pp. 686–707, Feb. 2019, doi: 10.1016/j.jcp.2018.10.045.

[5] C. Lorsung, Z. Li, and A. B. Farimani, “Physics informed token transformer for solving partial differential equations,” Mach. Learn.: Sci. Technol., vol. 5, no. 1, p. 015032, Feb. 2024, doi: 10.1088/2632-2153/ad27e3.

[6] Y. Liu, Z. Zhang, and H. Schaeffer, “PROSE: Predicting Operators and Symbolic Expressions using Multimodal Transformers.” arXiv, Sep. 28, 2023. doi: 10.48550/arXiv.2309.16816.

[7] C. Ying et al., “Do Transformers Really Perform Bad for Graph Representation?” arXiv, Nov. 23, 2021. doi: 10.48550/arXiv.2106.05234.

[8] M. Takamoto et al., “PDEBENCH: An Extensive Benchmark for Scientific Machine Learning.” arXiv, Mar. 13, 2023. doi: 10.48550/arXiv.2210.07182.

[9] J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proceedings of ICNN’95 - International Conference on Neural Networks, Nov. 1995, pp. 1942–1948 vol.4. doi: 10.1109/ICNN.1995.488968.

往期回顾

MindSpore AI科学计算系列 | 三维形状表征

MindSpore AI科学计算系列 | 生成扩散模型DiffDock显著提升分子对接准确率

MindSpore AI科学计算系列 | MeshGPT显著提升三维几何表示的质量

MindSpore AI科学计算系列 | MetNet3融合稀疏站点数据，实现提前24h天气预报