1.1 玻璃窗散热问题(复习题)
题目来源:《数学模型》(第五版)–姜启源、谢金星、叶俊
1.1.1 题目描述
北方旧宅改造时,为了增强保暖效果常用保温材料在外墙外面再加一层墙,假定只考虑热传导,试通过建模对改造后减少的热量损失给出定量分析,并获取有关数据进行计算。
1.1.2 题目分析
题目示意图如下图所示

我们已知
- 热量总是从温度高的一方传递向温度低的一方
- 热量的传递 Q Q Q与温度差 Δ \Delta Δ T T T成正比,与接触面积 S S S成正比,与墙体厚度 d d d成反比,于是有以下公式 Q = k S Δ T d Q = kS\frac{\Delta T}{d} Q=kSdΔT
1.1.3 模型假设
- 热量的传播过程只有传导,没有对流。假定墙体的密封性很好,两层墙体之间的空气是不流动的。
- 室内温度 T 1 T_1 T1和室外温度 T 2 T_2 T2保持不变,热传导过程已经处于稳定状态,即沿热传导方向,单位时间通过单位面积的热量是常数。
- 墙体材料均匀,热传导系数是常数。
1.1.4 模型
以单位面积通过的热量分析
双层墙
Q
1
=
k
1
∗
T
a
−
T
1
d
=
k
2
∗
T
b
−
T
a
l
=
k
1
∗
T
b
−
T
2
d
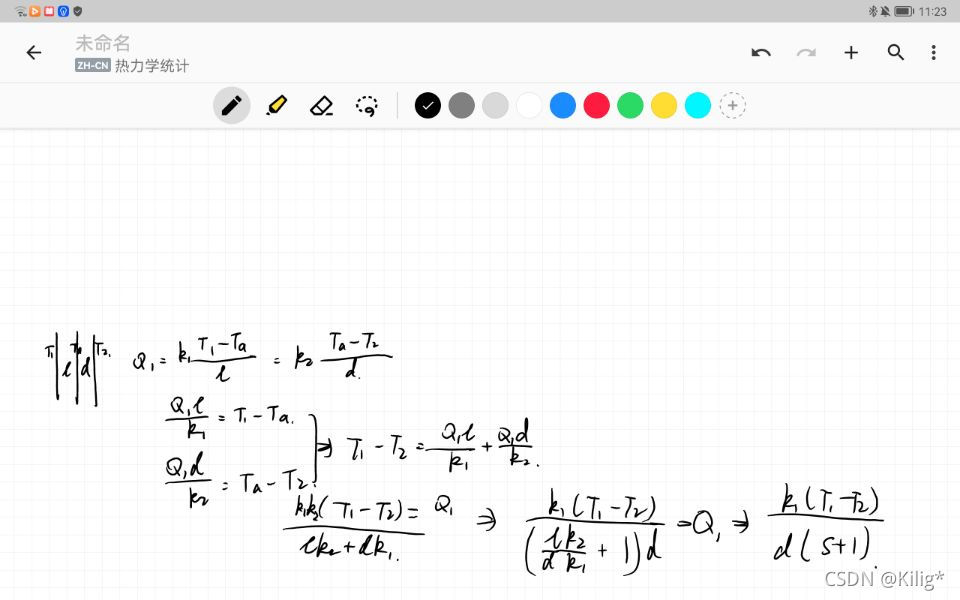
Q_1 =k_1*\frac{T_a-T_1}{d} = k_2 * \frac{T_b-T_a}{l} = k_1 * \frac{T_b-T_2}{d}
Q1=k1∗dTa−T1=k2∗lTb−Ta=k1∗dTb−T2
其中
k
1
k_1
k1为砖的热传导系数,
k
2
k_2
k2为墙体间空气的热传导系数,
d
d
d为墙体厚度,
l
l
l为墙体间距离。
式中消去
T
a
,
T
b
T_a,T_b
Ta,Tb可得
Q
1
=
k
1
∗
(
T
1
−
T
2
)
d
∗
(
s
+
2
)
,
s
=
h
∗
k
1
k
2
,
h
=
l
d
Q_1 =\frac{ k_1*(T_1-T_2)}{d*(s+2)}, s = h*\frac{k_1}{k_2},h = \frac{l}{d}
Q1=d∗(s+2)k1∗(T1−T2),s=h∗k2k1,h=dl
若使用同样多的材料建造单层墙,则墙体厚度为
2
d
2d
2d
Q
2
=
k
1
∗
T
1
−
T
2
2
d
Q_2 = k_1*\frac{T_1-T_2}{2d}
Q2=k1∗2dT1−T2
可得出二者之比为
Q
1
Q
2
=
2
s
+
2
\frac{Q_1}{Q_2} = \frac{2}{s+2}
Q2Q1=s+22
很显然
Q
2
>
Q
1
Q_2>Q_1
Q2>Q1,但是具体大多少,这取决于
s
s
s的大小,经查阅资料墙和不流通干燥空气的导热系数分别为
k
1
=
4.07
∗
1
0
−
4
K
J
/
(
m
⋅
s
⋅
K
)
k_1 = 4.07*10^{-4} KJ/(m \cdot s \cdot K)
k1=4.07∗10−4KJ/(m⋅s⋅K)
k
2
=
2.5
∗
1
0
−
5
K
J
/
(
m
⋅
s
⋅
K
)
k_2 = 2.5*10^{-5} KJ/(m \cdot s \cdot K)
k2=2.5∗10−5KJ/(m⋅s⋅K)
则有
s
=
16.28
∗
l
d
s = 16.28*\frac{l}{d}
s=16.28∗dl
1.1.5 灵敏度分析
则可绘制
Q
1
Q
2
\frac{Q_1}{Q_2}
Q2Q1 与
l
d
\frac{l}{d}
dl关系如下图

import numpy as np
import matplotlib.pylab as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 步骤一(替换sans-serif字体)
plt.rcParams['axes.unicode_minus'] = False # 步骤二(解决坐标轴负数的负号显示问题)
h = 40.7/2.5
#设 l/d = K
K = np.array([i/10 for i in range(1,70)])
s = 16.28*K
#设Q_1/Q_2 = Q_k
Q_k = 2/(s+2)
plt.figure(figsize=(10,5));
plt.title("$Q_1/Q_2$与$l/d$的关系")
plt.xlabel("$l/d$")
plt.ylabel("$Q_1/Q_2$")
plt.plot(K,Q_k,'-',label="$Q_1/Q_2$")
plt.legend()
plt.show()
可以看出在
l
d
<
2
\frac{l}{d} < 2
dl<2时,随着
l
d
\frac{l}{d}
dl变大
Q
1
/
Q
2
Q_1/Q_2
Q1/Q2迅速减少,但在
l
d
>
2
\frac{l}{d} > 2
dl>2时,
Q
1
/
Q
2
Q_1/Q_2
Q1/Q2下降的速度开始变的缓慢,因此选择
l
/
d
l/d
l/d在
1
∼
2
1\sim2
1∼2时较为合适,此时双层墙将比同样材料的单层墙降低热量散失10倍以上(类似于灵敏度分析)
博客题目考虑和教材答案有部分不一致教材未考虑墙间隙,而博客考虑了墙间隙,推导在↓

























 885
885

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










