二叉树经典面试题

最新推荐文章于 2024-09-23 21:07:30 发布

午饭要阳光

最新推荐文章于 2024-09-23 21:07:30 发布

阅读量2.2k

点赞数 16

分类专栏：刷题数据结构 c/c++基础文章标签：二叉树经典面试题

本文链接：https://blog.csdn.net/LF_2016/article/details/53221878

版权

c/c++基础同时被 3 个专栏收录

210 篇文章 152 订阅

订阅专栏

数据结构

59 篇文章 8 订阅

订阅专栏

刷题

42 篇文章 0 订阅

订阅专栏

以下二叉树的结点类型如下：

template<typename T>
struct BinaryTreeNode
{
	T _data;
	BinaryTreeNode<T> *_left;
	BinaryTreeNode<T> *_right;
	BinaryTreeNode(const T& data = T())
		:_data(data)
		, _left(NULL)
		, _right(NULL){}
};

1. 给你一颗普通的二叉树，求二叉树中最远的两个节点的距离

分析：

1、如果具有最远距离的两个结点之间的路径经过根结点，则最远距离就是这个根节点左边的深度加上根节点的右边的深度。

2、如果具有最远距离的两个结点之间的路径不经过根节点，则最远距离的结点就在根节点的某一棵子树上的两个叶子结点。

使用distance记录这个最远的距离。后序遍历二叉树中每一个结点，对于每一个结点先算出左边和右边的深度和然后与distance里面的数据进行比较，如果结果大于distance则更新distance的值。这种方法的时间复杂度是O(N)。

int _GetFarthestDistance(BinaryTreeNode<int>* root, int& distance)
{
	if (root == NULL)
		return 0;
	int left = _GetFarthestDistance(root->_left, distance);
	int right = _GetFarthestDistance(root->_right, distance);
	if ((right + left)> distance)
		distance = right + left;
	return left > right ? left + 1 : right + 1;
}

int GetFarthestDistance(BinaryTreeNode<int>* root)  //得到二叉树中距离最远的两个结点之间的距离
{
	assert(root);
	int distance = 0;
	_GetFarthestDistance(root, distance);
	return distance;
}

2. 由前序遍历和中序遍历重建二叉树（前序序列：1 2 3 4 5 6 - 中序序列:3 2 4 1 6 5）

分析：

先序遍历：访问当前结点，访问左子树，访问右子树.

中序遍历：访问左子树，访问当前结点，访问右子树.

可以发现，前序遍历的每一结点，都是当前子树的根节点，我们可以根据前序遍历的序列对中序遍历的序列进行划分。

如图：

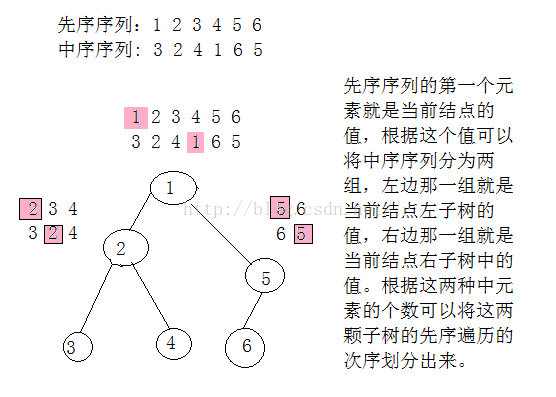
上面的分析只是针对于当树中没有重复出现的元素的情况，当有重复出现的元素的时候，要考虑到树的结构可能不唯一。

void CreatSubTree(BinaryTreeNode<int>* &root,
	int* InOrder,
	int *PrevOrder,
	int len)
{
	if (len<=0)
		return;

	root= new BinaryTreeNode<int>(PrevOrder[0]);
	int index = 0;           //父节点在数组中的下标
	for (; index < len; ++index)
	{
		if (PrevOrder[0] == InOrder[index])
			break;
	}
	int subTreeL =index;                     //左子树结点个数
	int subTreeR = len - index - 1;               //右子树结点个数
	CreatSubTree(root->_left, InOrder, PrevOrder + 1, subTreeL);
	CreatSubTree(root->_right,InOrder + index + 1, PrevOrder + index + 1, subTreeR);
}


BinaryTreeNode<int>* RebuildBinaryTree(int *InOrder, int *PrevOrder, int len)
{
	assert(InOrder);
	assert(PrevOrder);
	BinaryTreeNode<int>* root;
	CreatSubTree(root, InOrder, PrevOrder,len);
	return root;
}

3. 判断一棵树是否是完全二叉树

分析：

什么是完全二叉树呢？？？

如果一颗二叉树的只有最后两层结点的度能小于2，其余结点的度都等于2。且最后一层的结点从最左边依次排列。

如果一颗二叉树中的每一个结点都与编号从1到n的满二叉树中的结点一一对应，则称这棵二叉树为完全二叉树。

我们可以根据完全二叉树的定义，按照层序遍历一颗树，当遇到空结点时如果这棵树已经遍历完毕，则这棵树就是完全二叉树，如果遇到空结点的后面还有元素则这棵树就不是完全二叉树。

如图：

我们可以用一个flag来标记，当遇到第一个空结点是标记为1，如果后面要是再遇到非空结点时就表示不是完全二叉树。

bool IsCompleteBinaryTree(BinaryTreeNode<int>* root)  //判断一颗二叉树是否是完全二叉树
{
	if (root == NULL)
		return false;
	queue<BinaryTreeNode<int>*> q;
	int flag = 0;
	q.push(root);
	while (!q.empty())
	{
		BinaryTreeNode<int>* cur = q.front();
		q.pop();
		if (cur->_left)
		{
			if (flag)
				return false;
			q.push(cur->_left);
		}
		else
		{
			if (flag == 0)
				flag = 1;
		}
		if (cur->_right)
		{
			if (flag)
				return false;
			q.push(cur->_right);
		}
		else
		{
			if (flag == 0)
				flag = 1;
		}
	}
	return true;
}

4. 求两个节点的最近公共祖先

分析：

求两个结点的最近公共祖先有两种情况。

1、如果这两个结点不在一条线上，则它们就分别在最近的公共祖父的左右子树上。

2、如果这两个结点在一条线上，则它们之中深度最前的就是他们的最近的公共祖先。

方法1：

分别将两个结点的路径保存到两个数组中，然后比较这两个数组中的元素，第一个不相等的元素的前一个元素就是最近的公共结点。

例：

1、求2和3的最近的公共祖先

2的路径是：1 2

3的路径是：1 2 3

第三个元素不相同,所以最近的公共祖先是第二个元素，也就是2。

2、求3和5的最近公共结点

3的路径：1 2 3

5的路径：1 4 5

第2个元素不同，所以最近的公共结点是第一个元素，也就是1。

void _GetAncestor(BinaryTreeNode<int>* root,
	BinaryTreeNode<int>* node, 
	vector<BinaryTreeNode<int>* >& v,int &flag)
{
	if (root == NULL||flag==1)
		return;
	_GetAncestor(root->_left,node,v,flag);
	_GetAncestor(root->_right,node,v,flag);
	if (root == node || flag == 1)
	{
		v.push_back(root);
		flag = 1;
	}
}

BinaryTreeNode<int>* GetAncestor(BinaryTreeNode<int>* root,
	BinaryTreeNode<int>* node1,
	BinaryTreeNode<int>* node2)
{
	if (root == NULL || node1 == NULL || node2 == NULL)
		return NULL;
	vector<BinaryTreeNode<int>*> v1;     //保存从node1到root的路径
	vector<BinaryTreeNode<int>*> v2;     //保存node2到root的路径
	int flag = 0;
	_GetAncestor(root,node1,v1,flag);
	flag = 0;
    _GetAncestor(root, node2, v2, flag);
	vector<BinaryTreeNode<int>*>::reverse_iterator rv1 = v1.rbegin();
	vector<BinaryTreeNode<int>*>::reverse_iterator rv2 = v2.rbegin();
	while ((rv1!=v1.rend())&&(rv2!=v2.rend()))
	{
		if (*rv1 == *rv2)
		{
			rv1++;
			rv2++;
		}
		else
		{
			if (rv1!=v1.rbegin())
			--rv1;
			return *rv1;
		}
	}
	if (rv1 == v1.rend() && rv2 != v2.rend())
		return node1;
	if (rv1 != v1.rend() && rv2 == v2.rend())
		return node2;
	return NULL;
}

方法2：

给定一棵二叉树的头节点root,以及这棵二叉树的两个节点node1和node2,请返回node1和node2的最近公共祖先节点。我们可以后序遍历这棵树，用left记录左子树返回的结果，用right记录右子树返回的结果。

1、left和right都不为空时，返回当前结点cur。

2、当left和right有一个不为空时，返回不为空的那个结点。

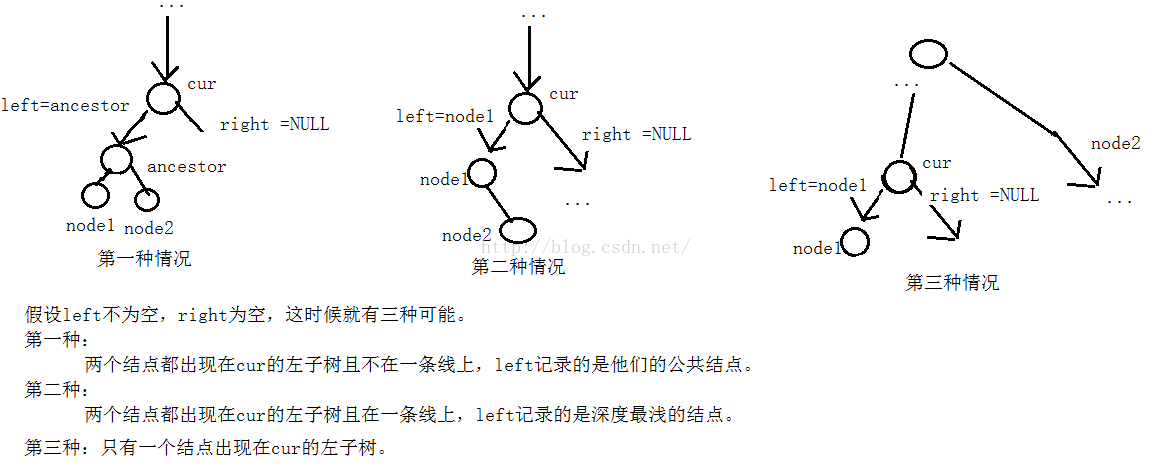
虽然是三种情况，但是不论是哪一种，只要返回left和right中不为空的就可以了。

3、当left和right都为空的时候，返回NULL。

BinaryTreeNode<int>* _GetAncestor(BinaryTreeNode<int>* root,
	BinaryTreeNode<int>* node1, 
	BinaryTreeNode<int>* node2)
{
	if (root == NULL)
		return NULL;
	BinaryTreeNode<int>* left=_GetAncestor(root->_left, node1, node2);
	BinaryTreeNode<int>* right=_GetAncestor(root->_right, node1, node2);
	if (left&&right)
		return root;
	if (root == node1)
		return node1;
	if (root == node2)
		return node2;
	if (left == NULL&&right)
		return right;
	if (right == NULL&&left)
		return left;
	return NULL;
}

BinaryTreeNode<int>* GetAncestor(BinaryTreeNode<int>* root,
	                             BinaryTreeNode<int>* node1,
	                             BinaryTreeNode<int>* node2)
{
	assert(root);
	assert(node1);
	assert(node2);
	BinaryTreeNode<int>* parent = NULL;
	BinaryTreeNode<int>* left =NULL;
	BinaryTreeNode<int>* right =NULL;
	parent=_GetAncestor(root,node1,node2);
	return parent;
}

5. 将二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向

分析：

二叉搜索树在中序遍历的时候是有序的，而且每一个结点都有左指针和右指针。我们可以让左指针left充当双向链表中的prev,右指针充当双向链表中的next。

方法1：

我们可以中序遍历这棵树，将中序得到的序列都保存到队列里面，然后再把队列里面的结点链接成一条链表，这样的话这条链表就是有序的了。

void _InOrder(Node<int>* root,queue<Node<int> *>& q)
{
	if (root == NULL)
		return;
	_InOrder(root->_left,q);
	q.push(root);
	_InOrder(root->_right,q);
}

void TreeToList(Node<int>* root)
{
	if (root == NULL)
		return;
	queue<Node<int> *> q;
	_InOrder(root,q);
	root = q.front();
	q.pop();

	root->_left = NULL;
	Node<int> * prev= root;
	while (!q.empty())
	{
		Node<int>* cur = q.front();
		q.pop();
		prev->_right = cur;
		cur->_left = prev;
		cur->_right = NULL;
		prev = cur;
	}
}

方法2：

中序遍历这棵树，利用一个prev指针，来记录前一个结点的值。将当前结点cur与prev进行链接。

void _Transfrom(Node<int>* root,Node<int>* &parent)
{
	if (root == NULL)
		return;
	_Transfrom(root->_left,parent);
	root->_left = parent;
	if (parent)
		parent->_right = root;
	parent = root;
	_Transfrom(root->_right,parent);
}

void TreeToList(Node<int>* root)
{
	//Node<int>* cur = root;
	Node<int>* parent = NULL;
	_Transfrom(root,parent);
	while (root->_left)
		root = root->_left;
}