吴恩达深度学习笔记之卷积神经网络(卷积网络)

1.1 计算机视觉（computer vision）

应用计算机视觉存在一个挑战：就是数据的输入可能会非常大，例如，过去一般的操作是64*64的小图片，实际上它的数据量是64*64*3，因为每张图片还有3个颜色通道，如果计算一下，可以得知数据量是12288，所以我们的特征向量X维度是12288，这其实不算大，但是如果操作更大的图片，比如一张1000*1000的图片，则其特征向量维度X为1000*1000*3，所以数字将会是300万，此时，假设隐藏层神经元个数也为1000，此时 矩阵是（1000，3m）为3billion，这是一个非常庞大的数字，会导致神经网络很容易发生过拟合，而且神经网络巨大的内存需求也让人不可接受。但是对于计算机视觉来说，我们肯定不希望它只能处理小图片，我们希望它能处理大图，为此，我们需要进行卷积运算，她是卷积神经网络中非常重要的一块。
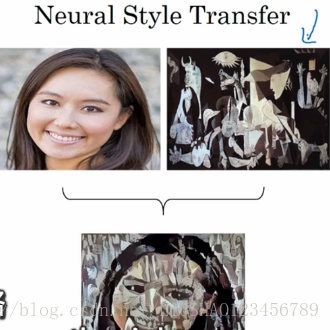
计算机视觉有如下几个应用：图片分类，目标检测，以及最近新出来的一种艺术形式，图片风格转换。

图片分类

风格转换

目标检测

1.2 边缘检测示例(Edge detection example)

卷积运算是卷积圣经网络中最最基本的组成部分，接下来我们使用边缘检测作为入门样例。

下图是具体细节：

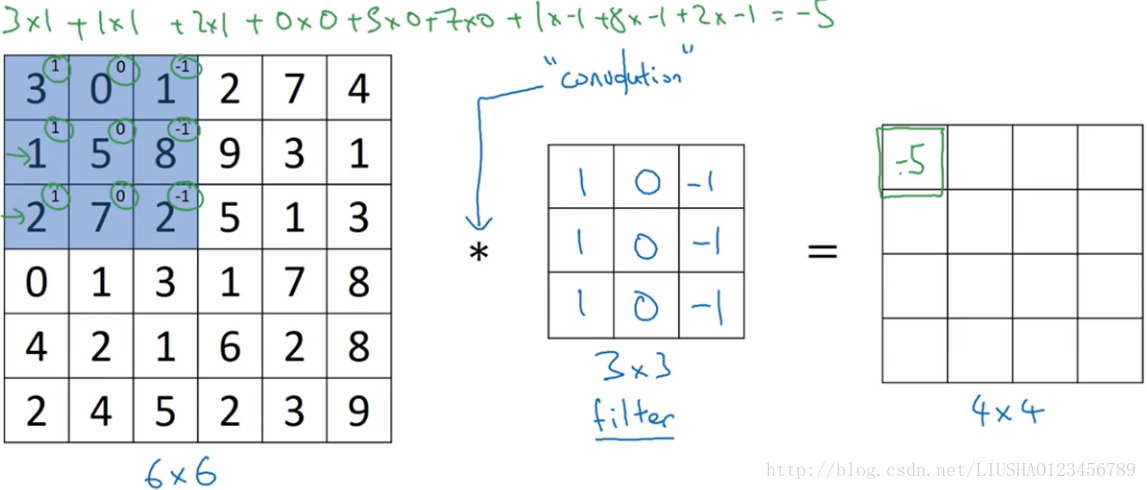
上图左边为一个二值图，故其为单通道，“*”表示一个卷积运算，它也是卷积运算的标准标志，中间的为一个过滤器，在论文中有时也称为核，右边是卷积得到的结果。以上就是一个垂直边缘检测器。为什么可以做垂直边缘检测呢，来看如下例子。

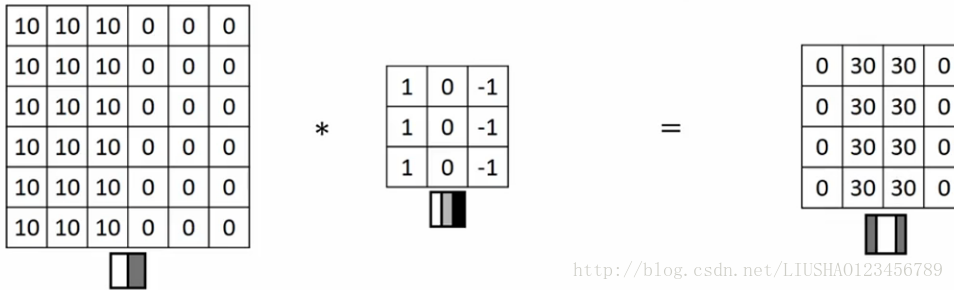
如果把右边看成一副图片，则右图下边的小图，像素值10是比较亮的一部分，左图右边像素值比较暗，在此使用灰色，这个图像里有特别明显的垂直边缘，这条垂直线是从黑到白的过度线。中间是一个过滤器，右图是结果，结果中我们可以看到垂直边缘检测出来了，但是检测到的边缘太粗，这是因为图片太小，如果我们用1000*1000的图片，我们会发现其会很好的检测出图像中的垂直边缘。

1.3 更多边缘检测例子(more edge detection)

上一节中已经见识到用卷积运算实现垂直边缘检测，在这节中，我们将学习如何区别正边到负边，这实际上就是由亮到暗于由暗到亮的区别，也就是边缘的过度。

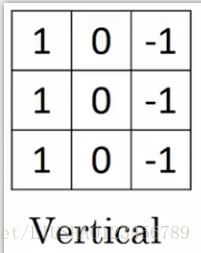
上图左边为一个垂直边缘过滤器，右边是水平边缘过滤器。通过使用不同的滤波器，可以找出垂直的或是水平的边缘。但实际上，对于这样一个3*3的滤波器来说，我们只使用了一种数字组合。但在历史当中，曾经争论过怎么样的数字组合才是最好的滤波器。我们还可以使用下面两种滤波器。

左图称为sobel filter，它的优点在于增加了中间一行元素的权值，会使得结果鲁棒性更高。右图则叫做scharr filter,他有着和之前完全不同的特性，实际上他也是一种垂直边缘检测。
随着深度学习的发展，就是当我们真正去检测复杂图像的边缘，我们不需要去使用研究者们所选择的这9个数字，我们可以把这9个数字当成9个参数，然后使用反向传播算法，让其去理解这9个参数，这样的话，可以得到一个出色的边缘检测。这种滤波器相比于单纯的垂直边缘和水平边缘，他可以检测出45°，70°，甚至是任何角度的边缘，可以将矩阵的所有数字都设置成参数，通过数据反馈，让神经网络自动去学习，学习到一些比较低级的特征。
如图所示：

1.4 padding

为了构建深度神经网络，我们需要学会的一个基本操作就padding。

在上一节中，我们知道边缘像素点只被一次输出所触碰或者所使用，但是中间的像素点会被使用多次。
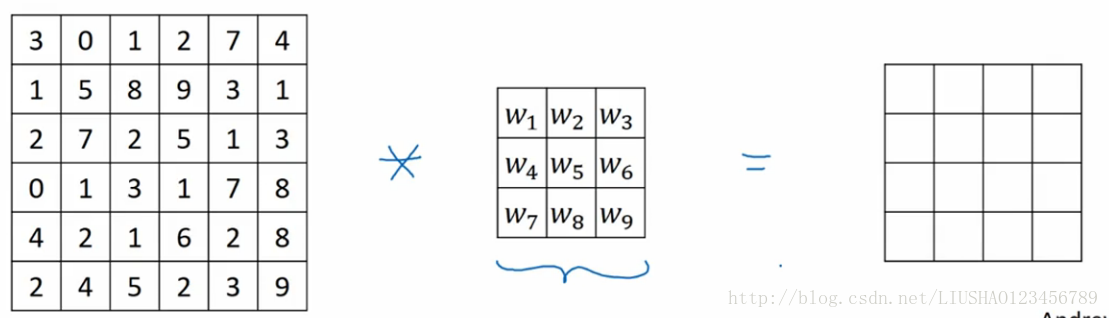
上一节中，如果我们用3*3的过滤器，卷积一个6*6的图像，最后会得到一个4*4的输出，这背后的数学解释是如果我们用n*n的图像，用一个f*f的过滤器做卷积，那么输出结果的维度是(n-f+1)*(n-f+1)。这样做如下两个缺点。

缺点一：

每次做卷积操作，图像就会缩小，从6*6缩小到4*4，经过几次卷积之后，图像会更小。直到可能变成1*1

缺点二：

如果我们注意角落边缘的像素，这个像素只被一个输出所触碰或者所使用，但是如果是中间的像素点就会有许多3*3的区域与之重叠，所以那些在角落或者边缘的区域的像素点，在输出中采用较少，意味着丢掉了图像边缘位置的许多信息。
为了解决以上两个缺点，我们可以在卷积操作之前，填充这副图像，在上述6*6矩阵中，再填充一层像素，此时就变成了8*8的图像，此时经过卷积之后，得到的输出不再是4*4，而依然是6*6的图像，习惯上我们用0去填充。至于填充多少像素，通常有两个选择。分别叫做valid卷积和same卷积。

valid卷积:

valid卷积意味着不填充，此时如果输入图像为n*n,过滤器为f f，则输出为(n-f+1)(n-f+1)

same卷积:

意味着填充之后，输入和输出之后大小是一样的。
根据上述公式，当我们填充p个像素点，此时输出大小为(n+2p-f+1)*(n+2p-f+1),为了让输入与输出相等即n+2p-f+1=n,可知

$${\rm{p}} = \left( {f - 1} \right)/2$$

所以当f是奇数时，只要选择相应的填充尺寸，就能确保得到和输入相同尺寸的输出。

1.5 卷积步长(strided convolutions)

我们首先看一个卷积步长的样例

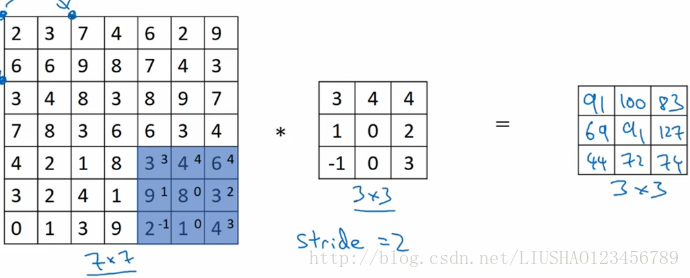
卷积中的步幅是另一个构建卷积神经网络的基本操作，输入和输出的维度由以下公式决定：
$$\left( {\frac{{n + 2p - f}}{s} + 1} \right) \times \left( {\frac{{n + 2p - f}}{s} + 1} \right)$$

s表示步长，如果商不是整数我们选择向下取整。

1.6 卷积中“卷”的体现指出(Convolutions over volumes)

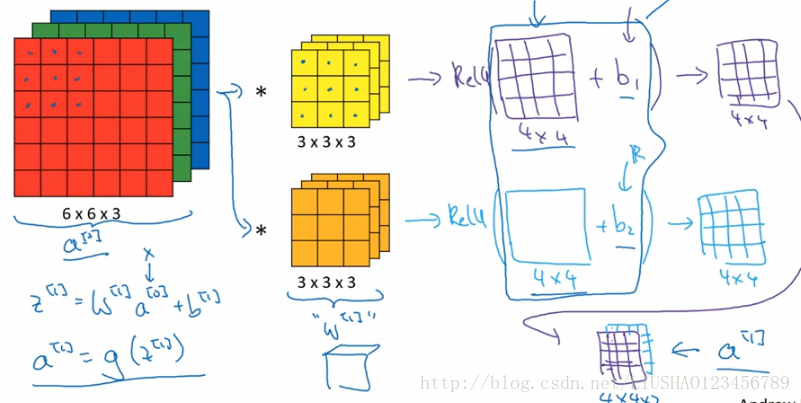
上节中讲到如何在灰度图上做卷积，这节中讲如何在彩色图中做卷积。为了检测图像的边缘，或者一些其他的特征，不是把他跟原来的3*3的过滤器做卷积，而是跟一个三维的过滤器做卷积，它的维度是3*3*3，对应红绿蓝三个通道。如图所示：

注意：图像的通道数和过滤器的通道数必须一致。

那么这个能干什么呢？

举个例子，这个过滤器是3*3*3，如果我们检测图像红色通道的边缘，那么我们可以将第一个过滤器设置为如下

而绿色通道全为0，蓝色通道也全为0，这样，如果我们把这三个堆叠在一起，形成一个3*3*3的过滤器，那么这就是一个检测边界，但只对红色通道有用。
按照计算机视觉的惯例，如果输入有不同的高，宽，过滤器也可以有不同的高，宽，但是通道数必须一样。
还有一个概念，对建立卷积神经网络至关重要，就是我们如果想同时检测垂直和水平边缘，还有45度或者70度边缘该怎么做。此时我们需要为过滤器设置深度。如图所示：

1.7 单层卷积网络（one layer of a convolutional network）

上节，我们知道了如何通过连个过滤器卷积处理一个三维图像，并输出两个4*4的矩阵，假设使用第一个过滤器进行卷积，得到一个4*4的矩阵，使用第二个过滤器得到另外一个4*4的矩阵，最终各自形成一个卷积神经网络层，然后增加偏差bias，它是一个实数，通过python广播机制，给这16个元素加上同一偏差，然后应用非线性函数Relu。同理，对第二个也进行同样的操作，并将两个4*4堆叠在一起，得到4*4*2的矩阵。具体流程如图所示：

Summary of notation

在这里就不具体写了，直接用图片来做总结

1.8 池化层(pooling layers)

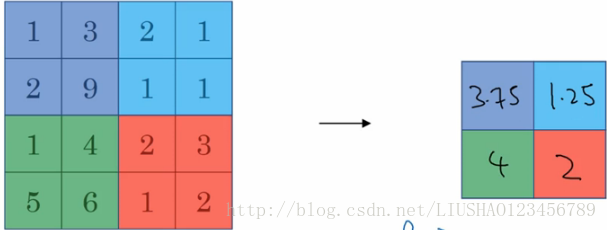
池化层可以缩减模型的大小，提高计算速度，同事提高所提取特征的鲁棒性。一般分为两种分别为max pooling 和 average pooling。我们首先来看最大池化。
最大池化作用实际就是，如果在过滤器中提取到某个特征，那么保留其最大值，绝大多数用的是最大池化，因为其实验效果比平均池化要好。如图为最大池化：

另一种为平均池化如图所示：

此外需要说明的是，池化层中包含两个超参数，如下：
f:filter size
s:stride
常用的参数值为f=2,s=2

1.9 why convolutions?

   和只用全连接层相比，卷积神经网络有两个优势分别为参数共享和稀疏连接。以下为一简单的卷积神经网络的架构。

由于不依赖于框架的卷积神经网络的代码叫长，这里就只粘贴一下基于tensorflow框架的简单卷积神经网络对mnist数据集的分类代码。如下：

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import input_data
mnist = input_data.read_data_sets('data/', one_hot=True)
trainimg   = mnist.train.images
trainlabel = mnist.train.labels
testimg    = mnist.test.images
testlabel  = mnist.test.labels
print ("MNIST ready")
n_input  = 784
n_output = 10
weights  = {
        'wc1': tf.Variable(tf.random_normal([3, 3, 1, 64], stddev=0.1)),
        'wc2': tf.Variable(tf.random_normal([3, 3, 64, 128], stddev=0.1)),
        'wd1': tf.Variable(tf.random_normal([7*7*128, 1024], stddev=0.1)),
        'wd2': tf.Variable(tf.random_normal([1024, n_output], stddev=0.1))
    }
biases   = {
        'bc1': tf.Variable(tf.random_normal([64], stddev=0.1)),
        'bc2': tf.Variable(tf.random_normal([128], stddev=0.1)),
        'bd1': tf.Variable(tf.random_normal([1024], stddev=0.1)),
        'bd2': tf.Variable(tf.random_normal([n_output], stddev=0.1))
    }
def conv_basic(_input, _w, _b, _keepratio):
        # INPUT
        _input_r = tf.reshape(_input, shape=[-1, 28, 28, 1])
        # CONV LAYER 1
        _conv1 = tf.nn.conv2d(_input_r, _w['wc1'], strides=[1, 1, 1, 1], padding='SAME')
        #_mean, _var = tf.nn.moments(_conv1, [0, 1, 2])
        #_conv1 = tf.nn.batch_normalization(_conv1, _mean, _var, 0, 1, 0.0001)
        _conv1 = tf.nn.relu(tf.nn.bias_add(_conv1, _b['bc1']))
        _pool1 = tf.nn.max_pool(_conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
        _pool_dr1 = tf.nn.dropout(_pool1, _keepratio)
        # CONV LAYER 2
        _conv2 = tf.nn.conv2d(_pool_dr1, _w['wc2'], strides=[1, 1, 1, 1], padding='SAME')
        #_mean, _var = tf.nn.moments(_conv2, [0, 1, 2])
        #_conv2 = tf.nn.batch_normalization(_conv2, _mean, _var, 0, 1, 0.0001)
        _conv2 = tf.nn.relu(tf.nn.bias_add(_conv2, _b['bc2']))
        _pool2 = tf.nn.max_pool(_conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
        _pool_dr2 = tf.nn.dropout(_pool2, _keepratio)
        # VECTORIZE
        _dense1 = tf.reshape(_pool_dr2, [-1, _w['wd1'].get_shape().as_list()[0]])
        # FULLY CONNECTED LAYER 1
        _fc1 = tf.nn.relu(tf.add(tf.matmul(_dense1, _w['wd1']), _b['bd1']))
        _fc_dr1 = tf.nn.dropout(_fc1, _keepratio)
        # FULLY CONNECTED LAYER 2
        _out = tf.add(tf.matmul(_fc_dr1, _w['wd2']), _b['bd2'])
        # RETURN
        out = { 'input_r': _input_r, 'conv1': _conv1, 'pool1': _pool1, 'pool1_dr1': _pool_dr1,
            'conv2': _conv2, 'pool2': _pool2, 'pool_dr2': _pool_dr2, 'dense1': _dense1,
            'fc1': _fc1, 'fc_dr1': _fc_dr1, 'out': _out
        }
        return out
print ("CNN READY")
a = tf.Variable(tf.random_normal([3, 3, 1, 64], stddev=0.1))
print (a)
a = tf.Print(a, [a], "a: ")
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
#sess.run(a)
x = tf.placeholder(tf.float32, [None, n_input])
y = tf.placeholder(tf.float32, [None, n_output])
keepratio = tf.placeholder(tf.float32)

# FUNCTIONS

_pred = conv_basic(x, weights, biases, keepratio)['out']
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(_pred, y))
optm = tf.train.AdamOptimizer(learning_rate=0.001).minimize(cost)
_corr = tf.equal(tf.argmax(_pred,1), tf.argmax(y,1)) 
accr = tf.reduce_mean(tf.cast(_corr, tf.float32)) 
init = tf.global_variables_initializer()

# SAVER
print ("GRAPH READY")
sess = tf.Session()
sess.run(init)

training_epochs = 15
batch_size      = 16
display_step    = 1
for epoch in range(training_epochs):
    avg_cost = 0.
    #total_batch = int(mnist.train.num_examples/batch_size)
    total_batch = 10
    # Loop over all batches
    for i in range(total_batch):
        batch_xs, batch_ys = mnist.train.next_batch(batch_size)
        # Fit training using batch data
        sess.run(optm, feed_dict={x: batch_xs, y: batch_ys, keepratio:0.7})
        # Compute average loss
        avg_cost += sess.run(cost, feed_dict={x: batch_xs, y: batch_ys, keepratio:1.})/total_batch

    # Display logs per epoch step
    if epoch % display_step == 0: 
        print ("Epoch: %03d/%03d cost: %.9f" % (epoch, training_epochs, avg_cost))
        train_acc = sess.run(accr, feed_dict={x: batch_xs, y: batch_ys, keepratio:1.})
        print (" Training accuracy: %.3f" % (train_acc))
        #test_acc = sess.run(accr, feed_dict={x: testimg, y: testlabel, keepratio:1.})
        #print (" Test accuracy: %.3f" % (test_acc))

print ("OPTIMIZATION FINISHED")