近世代数：阶，子群

阶的定义：a为G中的一个元素，a^n=e则N就叫a的阶。（最小的的正整数n，如果没有就叫无限阶）

a的阶用|a|.

定理一：有限群中的每个元素都有有限阶。

证明很简单：

 周期群，无扭群，混合群：

 m必是n的倍数。用反证法。

可以这样想：把n和k分成一块一块“砖”，一块砖就是最大公因数，n/这个最大公因数就是计算n是由几块砖组成的，简称砖数。再想想：把k往上重复n的砖数遍，再把n往上重复k的砖数遍，结果二者是不是一样高？这就意味着把a^k重复乘n的砖数遍后，结果相当于是a^n的几次幂，也就整出来了。

等等，k*n/(k,n)不就是k和n的最小公倍数吗，我傻了。

这个可以直接看出来，感觉不用证。

这里是把1当成砖了，所以n的砖数就是n自己。

老道理，(m,n)=1,最小公倍数就是mn,所以只能这样。

就是在交换群里，每个元素都可以乘m次变e，阶数都是m的因数。记得任意a,b一定有x使bx=a结论吗？往里带就行。

子群：

从这个定义可以看出来，只要|G|(G的元素个数的意思，不是阶数，群哪来阶数)>1,至少有两个子群。首先是{e}，完美符合群的定义。还有G自己也是子群。（注意子群的代数运算是一样的 ）

这两个子群称为群G的平凡子群。别的子群，如果存在的话，叫做G的非平凡子群或真子群。

大家用的是同一个运算嘛。

保证不出家门（a-1在H里可以保证e也在家里）

中心元素：

可换就是“aob=boa”的意思。

解释一下：GL(F)是一般线性群，一般线性群是指基域K上n×n 可逆矩阵全体组成的矩阵乘法群。

特殊线性群就是对应行列式等于1的。

纯量矩阵就是kE,单位矩阵的倍数。

中心：

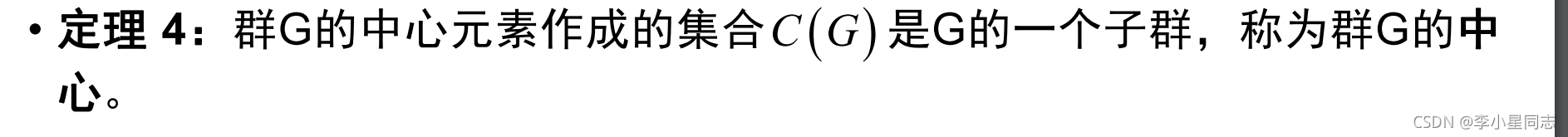
 下面这个结论也很好看出来。

自己乘自己跳不出那个圈子，还是自己。自己逆自己也一样 

反过来推，ab属于h,a-1还属于h,那可不就成了子群了吗。

 有没有一点像证明子群？ab-1属于h的套路又来了。