一、实验目的
1、 熟练理解树和二叉树的相关概念,掌握的存储结构和相关操作实现;
2、 掌握树的顺序结构的实现;
3、 学会运用树的知识解决实际问题
二、 实验内容
自己确定一个二叉树(树结点类型、数目和结构自定)利用顺序结构方法存储。实现树的构造,并完成:
1)层序输出结点数据;
2)以合理的格式,输出各个结点和双亲、孩子结点信息;
3)输出所有的叶子结点信息;
4)分析你的算法对于给定的二叉树的存储效率。
三、算法分析
1、定义tree类,长度为100的字符型数组,利用数组存放二叉树的结点信息。
2、print()层序输出不为空的结点,leaf()输出所有叶子结点信息,cp()查询结点双亲和孩子信息。
四、代码
#include<iostream>
using namespace std;
const int MaxSize=100;
class tree
{
private:
char data[MaxSize];
int length;
public:
~tree(){}
tree(char a[],int n);
void print();
void leaf();
void cp(int i);
};
tree::tree(char a[],int n)
{
int last=0;
if(n>=MaxSize) throw"full";
for(int i=0;i<n;i++)
{ data[i]=a[i];
length=n;
}
}
void tree::print()
{
for(int i=0;i<length;i++)
{if(data[i]!='1')
cout<<data[i]<<" ";}
cout<<endl;
}
void tree::cp(int i)
{
if(data[2*i-1]!='1'&&2*i-1<length&&data[i-1]!='1') cout<<"左孩子:"<<data[2*i-1]<<endl;
else cout<<"没有左孩子!"<<endl;
if(data[2*i]!='1'&&2*i<length&&data[i-1]!='1') cout<<"右孩子:"<<data[2*i]<<endl;
else cout<<"没有右孩子!"<<endl;
cout<<"双亲为:"<<data[i/2-1]<<endl;
}
void tree::leaf()
{
for(int i=1;i<=length;i++)
if(data[i-1]!='1'&&data[2*i-1]=='1'&&data[2*i]=='1') cout<<data[i-1]<<" ";
}
void main()
{
char t[13]={'A','B','C','1','D','E','1','1','1','F','1','1','G'};
tree T(t,13);
T.print();
T.leaf();
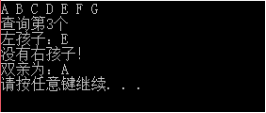
cout<<"查询第3个"<<endl;
T.cp(3);
}
六、总结
用顺序存储结构方法存储二叉树和顺序表差不多。
当二叉树为完全二叉树或满二叉树时,存储效率较高;当其为右斜树时,存储效率最低。






















 1613
1613

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








