问题
河蟹先生将要给与他们一篇从互联网上收集来的文章,和一本厚厚的河蟹词典,而他们要做的是判断这篇文章中是否存在那些属于河蟹词典中的词语
朴素方法:枚举每一个单词,然后枚举文章中可能的起始位置,然后进行匹配,看能否成功。如果说词典的词语数量为N,每个词语长度为L,文章的长度为M,时间复杂度O(M*N*L)
利用trie树的优化方法:对字典建立trie树,判断是否从某个起始位置开始的一段字符(也就是从这个起始位置开始的字符串的一个前缀字符串),它存在于“河蟹”词典里面 ?时间复杂度O(M*L)
Trie树的优化思路——后缀结点
我们在算法过程中,先枚举第一个字符作为起始位置,并最多匹配到第k个字符,因为str[1..k]这一段在tree中对应的结点A结点没有str[k+1]这一条边。这时候我们便要枚举第二个字符作为起始位置,并最多匹配到第k2个字符,这同样是因为str[2..k2]这一段在tree中对应的结点B结点没有str[k2+1]这一条边。也就是说我们在最开始的计算中,要先从tree的0号结点走到A结点,然后回到0号结点,再走到B结点。
如果我们从str的当前起点开始,匹配了l个长度走到了A结点,如果我们把A结点对应的字符串(即从tree的0号走到A结点的路径)去掉第一个字符,形成一个新的字符串,那么这个字符串肯定是和从str的下一个起点开始,长度为l-1的子串是一样的,而如果我们能够预先找到这个字符串在tree中对应的结点B’,我们就不用像之前所说的那样从0号节点走到A结点然后回到0号结点再走到B结点,而是可以直接从0号结点走到A结点然后直接跳转到B’结点然后再根据从str[i+l..k1]这一段走到B结点。
我们的问题变成了:如何对于一棵给定的Trie树,找到其中每一个结点对应的后缀结点——这个结点在Trie中对应路径去掉第一个字符之后在Trie中对应的结点。
如何求解Trie树中每个结点的后缀结点
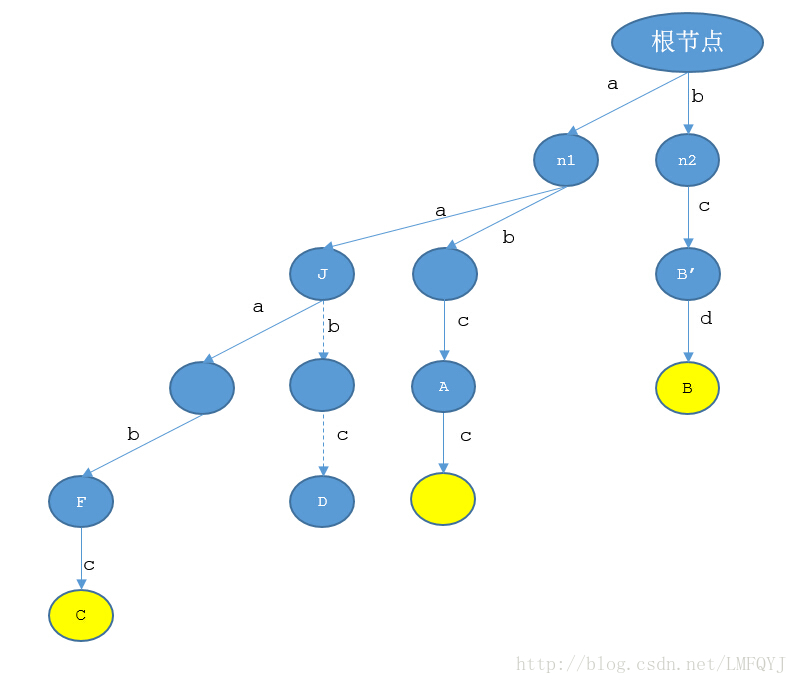
如图所示,现在求C的后缀结点,如果tree中存在一个结点D,其对应的路径是aabc,那么这个结点的后缀结点应该是结点A,既然结点D是不存在的,那么就意味着这个开始结点的枚举,是肯定在中途就要找不到的,所以直接从C结点跳转到A结点就可以了。这时又有一个问题,如果从tree的根节点到D结点的路径中有标记结点怎么办?如果有标记结点,相当于被忽略掉了,这就要引进一个新的概念,后缀结点为标记结点的结点也需要被标记。
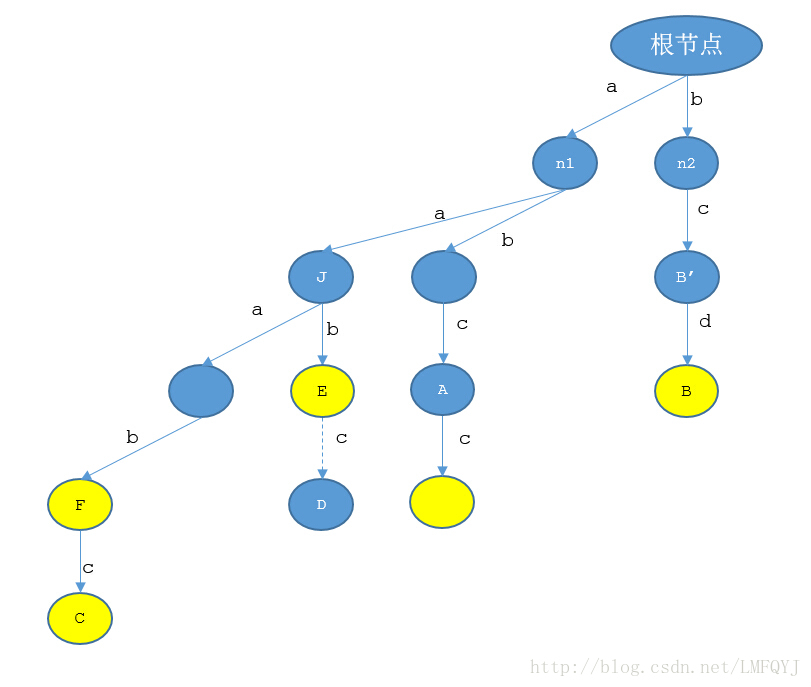
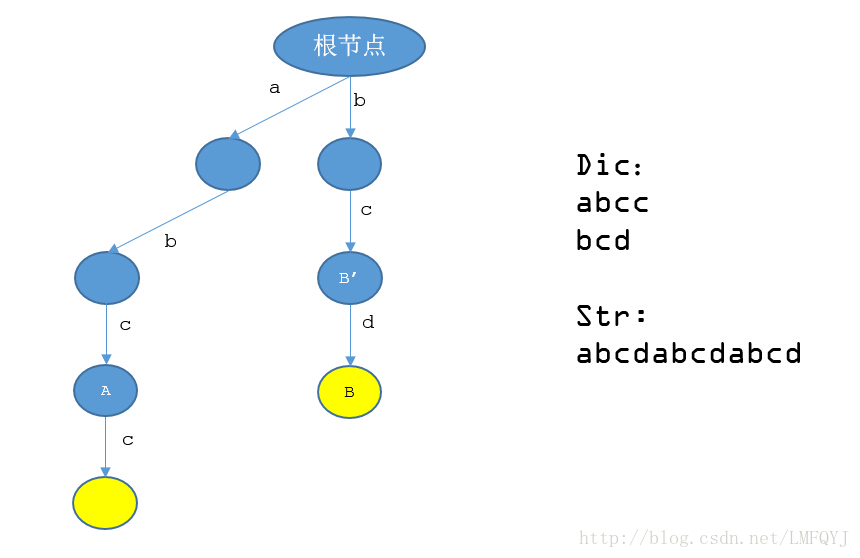
下面我们来计算后缀结点
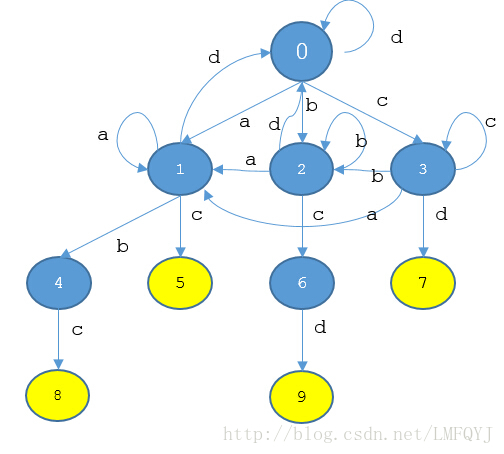
“如果用trie(X)表示X的根节点,next(X)(‘a’)表示从X出发标号为’a’的边指向的结点,我们可以知道trie(0)=0, next(0)(‘a’)=1, next(0)(‘b’)=2, next(0)(‘c’)=3, next(0)(‘d’)=0。”
“由于trie(1)=0, 我们可以补上从1出发的’a’,’d’这两条边:next(1)(‘a’)=next(0)(‘a’)=1, next(1)(‘d’)=next(0)(‘d’)=0”
“由于trie(2)=0, 我们可以补上从2出发的’a’,’b’,’d’这三条边:next(2)(‘a’)=next(0)(‘a’)=1, next(2)(‘b’)=next(0)(‘b’)=2, next(2)(‘d’)=next(0)(‘d’)=0”
“由于trie(3)=0, 我们可以补上从3出发的’a’,’b’,’c’这三条边:next(3)(‘a’)=next(0)(‘a’)=1, next(3)(‘b’)=next(0)(‘b’)=2, next(2)(‘c’)=next(0)(‘c’)=3”
“由于trie(4)=next(trie(1))(‘b’)=2, 我们可以补上从4出发的’a’,’b’,’d’这三条边:next(4)(‘a’)=next(2)(‘a’)=1, next(4)(‘b’)=next(2)(‘b’)=2, next(4)(‘d’)=next(2)(‘d’)=0”
例题
输入
每个输入文件有且仅有一组测试数据。
每个测试数据的第一行为一个整数N,表示河蟹词典的大小。
接下来的N行,每一行为一个由小写英文字母组成的河蟹词语。
接下来的一行,为一篇长度不超过M,由小写英文字母组成的文章。
输出
对于每组测试数据,输出一行”YES”或者”NO”,表示文章中是否含有河蟹词语。
样例输入
6
aaabc
aaac
abcc
ac
bcd
cd
aaaaaaaaaaabaaadaaac
样例输出
YES
#include<iostream>
#include<cstring>
#include<string>
#include<queue>
using namespace std;
struct Trie{
int flag;
struct Trie *next[26];
struct Trie *suffix;
Trie(){
flag=0;
memset(next,NULL,sizeof(next));
suffix=NULL;
}
};
void build(Trie *root, string &s){
Trie *cur=root;
int len=s.length();
for(int i=0;i<len;++i){
int id=s[i]-'a';
if(!cur->next[id]){
Trie *nn=new Trie();
cur->next[id]=nn;
}
cur=cur->next[id];
}
cur->flag=1;
}
int main(){
int n;
cin>>n;
string s;
Trie *root=new Trie();
while(n--){
cin>>s;
build(root,s);
}
root->suffix=root;
queue<Trie*> qt;
for(int i=0;i<26;++i){
if(!root->next[i])
root->next[i]=root;
else{
root->next[i]->suffix=root;
qt.push(root->next[i]);
}
}
Trie *cur, *suf;
while(!qt.empty()){
cur=qt.front();
suf=cur->suffix;
qt.pop();
for(int i=0;i<26;++i){
if(!cur->next[i]){
cur->next[i]=suf->next[i];
}else{
cur->next[i]->suffix=suf->next[i];
qt.push(cur->next[i]);
}
}
}
cin>>s;
int len=s.length(),flag=0;
cur=root;
for(int i=0;i<len;++i){
int id=s[i]-'a';
cur=cur->next[id];
if(cur->flag) {
cout<<"YES"<<endl;
flag=1;break;
}
}
if(!flag) cout<<"NO"<<endl;
return 0;
}





















 928
928

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








