并查集应用及Kruskar算法

一、定义：

并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查找问题。在一些有N个元素的集合应用中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。

应用很多，比如求无向图的连通分量个数，最完美的当属实现Kruskar算法求最小生成树

二、并查集基础（三种基本操作）：

     在一些应用中，要将n个不同的元素分成一组不相交的集合。

    并查集的两个重要操作：找出给定元素所属的集合、合并两个集合，即查询和合并功能。并查集经常在使用中以森林来表示。

(1)、MAKE_SET(x)：建立一个新的集合，其唯一成员为x。每个元素的父节点是它本身，秩为0

     MAKE_SET(x)

       p[x] = x

       rank[x] = 0;

(2)、UNION(x,y)：将包含x和y的两个集合合并为一个新的集合。

    如果连个节点的秩不同，则秩大者为父节点。

    如果两个相同，任选之一使其秩加1，并作为父节点。

    注：按秩合并的目的是使得合并后的树高度相对较小。

 

(3)、FIND_SET(x)：返回一个指针，指向包含x的集合的代表。

    查找元素的集合即是查找这个元素所在集合的祖先，这是并查集判断和合并的最终依据。

    判断两个元素是否属于同一个集合，只要看他们的祖先是否相同即可。

    FIND_SET(x)

    1）、method 1：只是找到x的祖先节点

    if x != p[x]

         then x <-- FIND_SET(p[x])

    retrun x

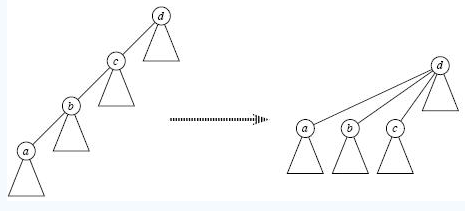
    2）、method 2: 找到祖先节点的同时，把每个子孙都直接指向祖先节点，下次再查找时减少查找时间到O(1)。如下图所示：

    if x != p[x]

       then p[x] <-- FIND_SET(p[x])

    retrun p[x]

三：应用

3.1、问题：HDU 1232 畅通工程

某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？ 

Input：

测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。 
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时，输入结束，该用例不被处理。

Output：

对每个测试用例，在1行里输出最少还需要建设的道路数目

分析：目前各个城市之间的道路可以视为有n个不同的集合，每个集合里的城市通过路连接，我们只需要把不同的集合连起来即可，同时也就是求有多少个集合存在。

#include<iostream>
#include<cstdio>
using namespace std;
 
int parent[1002];   //parent[x]表示x的父节点
int rank[1002];     //rank[x]表示x的秩
 
//查找集合 
int Find(int x){
    while (parent[x] != x) {
        x = parent[x];
    }
    return x;
}

//查找方法2，查找的同时进行路径压缩，递归版
int Find2(int x){
    while(parent[x] != x){
        parent[x] = Find2(parent[x];
    }
    return parent[x];
}
 
/非递归版路径压缩
int Find3(int n) {//r->root
    int r = n;
    while (r != root[r]) {//寻找根结点
        r = root[r];
    }
    int x = n, y;
    while (x != r) {//压缩路径，全部赋值为根结点的值  
        y = root[x];
        root[x] = r;
        x = y;
    }
    return r;
}

//合并操作 
//简化操作，因为只是为了求一共有多少个集合，合并操作就是最简单的操作，没有保存秩数组
void Union(int x, int y) {
    x = Find(x);
    y = Find(y);
    if(x == y)
        return;
    if(x != y) {
        parent[x] = y; 
    }
}

//合并操作，更新秩
void Union2(int x, int y){
    x = Find(x);
    y = Find(y);
    if(x == y)
    return;
    if(rank[x] > rank[y])
        parent[y] = x;
    else{
        parent[x] = y;
        if(rank[x] == rank[y])
            rank[y]++;
    }
}
 
int main() {
    int n, m;
    while(~scanf("%d", &n), n) {
        //建立集合 
        for(int i = 1; i <= n; i++) {
            parent[i] = i;
        }
         
        scanf("%d", &m);
        while (m--) {
            int x, y;
            scanf("%d %d", &x, &y);
            Union(x, y);
        }
         
        //计算不相交集合数 
        //只需要查找有多少个节点的父节点是自己即可
        int cnt = 0;
        for(int i = 1; i <= n; i++) {
            if(parent[i] == i) {
                cnt ++;
            }
        }
        printf("%d\n", cnt - 1); //总路径为集合数-1
    }
}

3.2：实现Kruskar算法

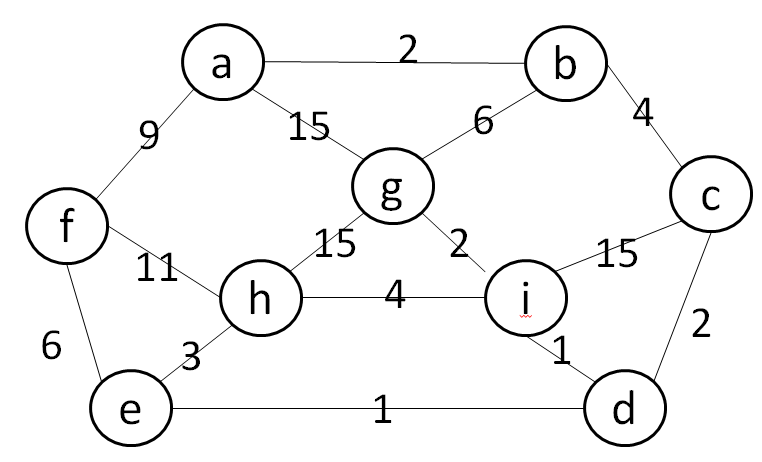
Kruskar算法是找出森林中连接任意两棵树的所有边中，具有最小权值的边（u,v)作为安全边，并把它添加到正在生长的森林中，它是一种贪心算法，因为在算法中的每一步中，添加到森林中的边的权值都是尽可能最小的。

思路：

1、设连通图为N=(V,{E})，令最小生成树初始状态为只有n个顶点而无边的非连通图T=(V,{F})，每个顶点即可用一个并查集表示

2、在边集合E中选取代价最小的边，加入到T中，即合并边两端顶点所属的并查集

3、以此类推，直到T中有n-1条边即可

#include <iostream>
#include <vector>
#include <algorithm>
#include <functional>
#include <conio.h>
using namespace std;

#define	MAX_NUM 1000 //MAX_NUM表示点,边的最大个数
#define WQ 9999 //wq表示两点的距离为无穷
int mix[MAX_NUM][MAX_NUM]; //邻接矩阵存储相应的边的权重

//9*9,图的路径，邻接矩阵表示图
int Graph[MAX_NUM][MAX_NUM]={
	{WQ, 2,WQ,WQ,WQ, 9,15,WQ,WQ},
	{ 2,WQ, 4,WQ,WQ,WQ, 6,WQ,WQ},
	{WQ, 4,WQ, 2,WQ,WQ,WQ,WQ,15},
	{WQ,WQ, 2,WQ, 1,WQ,WQ,WQ, 1},
	{WQ,WQ,WQ, 1,WQ, 6,WQ, 3,WQ},
	{ 9,WQ,WQ,WQ, 6,WQ,WQ,11,WQ},
	{15, 6,WQ,WQ,WQ,WQ,WQ,15, 2},
	{WQ,WQ,WQ,WQ, 3,11,15,WQ, 4},
	{WQ,WQ,15, 1,WQ,WQ, 2, 4,WQ}
};

//定义边结构体
typedef struct edge{
	int w;  //权值
	int v1; //顶点1
	int v2; //顶点2
	bool operator < (const edge& e) const //重载大小判断函数，方便使用sort函数进行向量的排序
	{
		return w < e.w;
	}
	bool operator > (const edge& e) const
	{
		return w > e.w;
	}
}Edge;

//并查集
int setParent[MAX_NUM]; //存储节点的父节点，用于判断不同节点是否属于同一集合  
int setRank[MAX_NUM];   //存放节点的秩

void make_set(int x)
{
	setParent[x] = x;
	setRank[x] = 0;
}

int find_set(int x)
{
	if( x != setParent[x])
		setParent[x] = find_set(setParent[x]);
	return setParent[x];
}

void union_set(int x,int y)
{
	x = find_set(x);
	y = find_set(y);
	if(x == y) return;
	if(setRank[x] > setRank[y])
	{	
		setParent[y] = x;
	}
	else
	{
		setParent[x] = y;
		if(setRank[x] = setRank[y])
		{
			setRank[y]++;
		}
	}
}

void Kruskal(int n)
{
	int i,j;
	int k = 0;
	//构造并查集，每个顶点为一个集合
	for(i=0; i<n; i++)
	{
		make_set(i);
	}
	//初始化图的各个边，所有边用vector存放
	vector<Edge> vEdge;
	for(i=0; i<n-1; i++)
	{
		for(j=i+1; j<n; j++)
		{
			if(Graph[i][j] != WQ)
			{
				Edge tmpEdge = {Graph[i][j],i,j};
				vEdge.push_back(tmpEdge);
				k++;
			}
		}
	}
	//根据权值对所有边进行排序
	sort(vEdge.begin(),vEdge.end(),less<Edge>());

	i = j = 0;

	while(j<k && i<n-1)
	{
		Edge tmpEdge = vEdge[j];
		//如果一条边的两个顶点不属于同一集合，则合并两个集合，即添加该边为最小生成树的一条路径
		if(find_set(tmpEdge.v1) != find_set(tmpEdge.v2))
		{
			union_set(tmpEdge.v1,tmpEdge.v2);
			i++;
			cout << char(tmpEdge.v1 + 'a') << "\t" << char(tmpEdge.v2 + 'a') << "\t" << tmpEdge.w << endl;
		}
		j++;
	}
}

int main()
{
	Kruskal(9);

	system("pause");
 	return 0;
}

本文主要参考  http://mindlee.net/2011/10/21/disjoint-sets/#jtss-qzone 以及 http://blog.csdn.net/kyle_once/article/details/6171839?reload 

然后自己归纳总结而出