比如说,我们要在一个无重复数据的数组中寻找一个指定的元素,那么最简单的方法就是直接for循环一遍暴力查找即可
时间复杂度为O(n),花费时间为线性时间,而现在如果我们把这个常规问题抽象化,即
在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
这样的问题看起来似乎很简单,每次直接暴力查找即可,但是我们需要注意的问题是,在数据量非常大的情况下,那么时间复杂度将达到O(N*n)(n为查询次数),那么这类问题在实际应用中,如果采取上述方法去做的话,耗费的时间将是巨大的。而如果用常规的数据结构去解决该类问题的话(顺序结构,普通树结构等),那么计算机在空间上也无法承受。所以,并查集这种数据结构便应运而生了。
1.并查集的基本概念:
首先我们要给并查集下一个比较确切的概念:
下面是百度百科给并查集下的概念:
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。集就是让每个元素构成一个单元素的集合,也就是按一定顺序将属于同一组的元素所在的集合合并。
2.并查集的一些基本操作:
了解了并查集的一些基本概念之后,那么必然涉及到并查集的一些基本操作(就像我们一开始学习链表这种数据结构时,在了解了基本概念之后,都会涉及到该种数据结构的一些基本操作),下面是并查集的几种基本操作:
1.MAKE-SET(x):即初始化操作,建立一个只包含元素 x 的集合。
通常并查集初始化操作是对每个元素都建立一个只包含该元素的集合。这意味着每个成员都是自身所在集合的代表,所以我们只需要将所有成员的父结点设为它自己就好了。
2.UNION(x, y):即合并操作,将包含 x 和 y 的集合合并为一个新的集合。
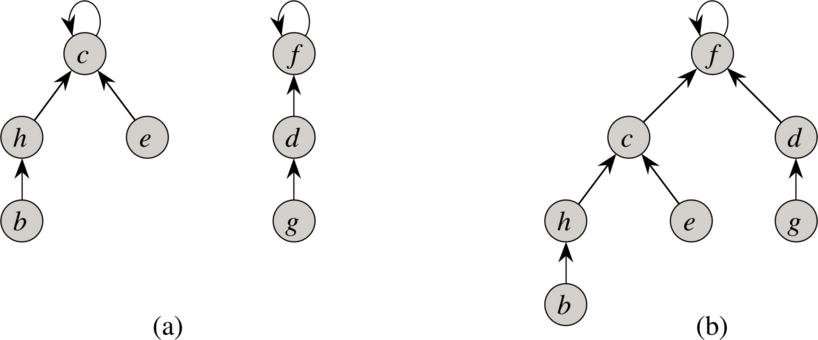
并查集的合并操作需要用到查询操作的结果。合并两个元素所在的集合,需要首先求出两个元素所在集合的代表元素,也就是结点所在有根树的根结点。接下来将其中一个根结点的父亲设置为另一个根结点。这样我们就把两棵有根树合并成一棵了。
如上图所示,图(a)为两个合并前的集合对应的不相交森林,两个集合对应的有根树的根分别是 c 和 f。我们将两个集合进行合并,就会得到图(b)所示的新集合,集合对应的有根树的根为 f。
3.FIND-SET(x):即查询操作,计算 x 所在的集合。
在不相交森林中,并查集的查询操作,指的是查找出指定元素所在有根树的根结点是谁。我们可以通过每个指向父结点的边回溯到结点所在有根树的根,也就是对应集合的代表元素。
并查集的查询操作最坏情况下的时间复杂度为O(n),其中 n 为总元素个数。最坏情况发生时,每次合并对应到森林上都是一个点连到一条链的一端。此时如果每次都查询链的最底端,也就是最远离根的位置的元素时,复杂度便是O(n)了。
为了改善时间效率,可以通过启发式合并方法,将包含较少结点的树接到包含较多结点的树根上,可以防止树退化成一条链。另外,我们也可以通过路径压缩的方法来进一步减少均摊复杂度。同时使用这两种优化方法,可以将每次操作的时间复杂度优化至接近常数级。
3.并查集森林:
通常我们会用有根树来表示集合,树中的每一个结点都对应集合的一个成员,每棵树表示一个集合。
每个成员都有一条指向父结点的边,整个有根树通过这些指向父结点的边来维护。每棵树的根就是这个集合的代表,并且这个代表的父结点是它自己。
通过这样的表示方法,我们将不相交的集合转化为一个森林,也叫不相交森林。
根据上面对并查集的描述,那么我们能够得到一些并查集的性质:
1.通常我们用森林来表示并查集,一棵有根树表示一个集合
2.如果 a 和 b 属于一个集合,b 和 c 属于一个集合,(a和b 以及 b和c同属的集合属于不相交集合,即这两个集合要么是同一个集合,要么这两个集合相交部分为空),则 a 和 c 也属于一个集合
3.不加优化的并查集,最坏情况下查询的时间复杂度为O(n)
那么在有了以上的叙述之后,我们就要着手实现代码了:
首先我们先要声明两个数组,分别用于记录当前操作节点的父亲节点和作为根节点时整棵树的大小(也叫树的秩):
#define size 101
int father[size],rank[size];在存储结构确定了之后,那么我们则要对每个节点的父亲节点初始化并且赋予秩的值:
//并查集初始化操作
void Init(int N){
int i;
for(i = 1;i < N;++i){
father[i] = i;
rank[i] = 1; //father[i]用于记录节点i的父亲节点,而rank[i]则用于记录
//节点i作为根节点时整棵树的大小(也称权重,用于记录树的节点个数)
}
}那么当初始化操作确定之后,我们要做的就是查询和合并操作了,如果待查询的两个数据中集合的代表数据(即树的根)不是同一个的话,那么我们则需要将这两个集合合并成一个(即将两棵有根树合并成一棵有根树,这样的话方便后续数据的查询),而合并操作则要涉及到怎么样将两棵树合并才能使得后序的查询操作遍历树节点的次数尽量少?那么这里就涉及到了这两个集合中代表元素的权重问题了。
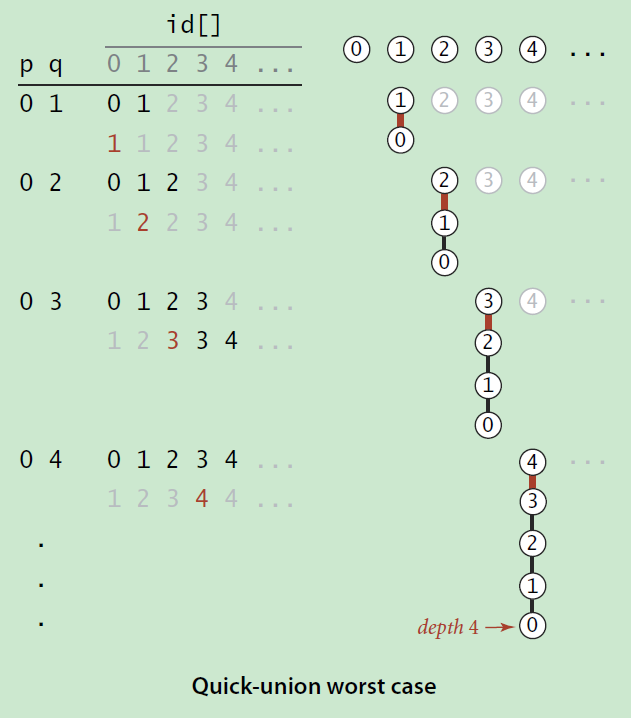
首先我们分析,如果不对两棵有根树的权重加以判断,而是随意连接两棵树的根,将其合并成一棵有根树,那么在最坏的情况下,最后n个元素合并之后,树结构可能会退化成了链结构:
图片来自《算法》(第四版)
如上图所示,这样的话在后续查询操作中,查询操作的最坏时间复杂度则依然还是线性复杂度O(n)
那么为了防止这样的问题出现,我们则需要在每次合并操作时,判断两棵树根节点的权重,然后再将权重小的根节点指向权重大的根节点(即将小树指向大树)
原因其实很简单:当把小树接至大树上时,那么大树上的节点寻找根节点的操作次数不变,而小树上的节点寻找根节点的操作次数各加1即可。那么总的增加的次数即为小树的节点数。
而如果反过来,把大树接至小树上时,那么小树上的节点寻找根节点的操作次数不变,而大树上的节点寻找根节点的操作次数各加1,那么总的增加的次数即为大树的节点数。
根据以上分析,为了尽量增加寻找根节点时的查询效率,那么显然是将权重小的根节点指向权重大的根节点(即将小树指向大树)
有了这样的分析之后,那么我们就可以将查询和合并操作封装成两个完整的函数:
//并查集的查询操作,查询当前操作到的节点的根节点
//在查询操作中,我们需要将查询的过程压缩,即减少向上遍历询问次数
//那么一般情况下会采取路径压缩的做法
//路径压缩:就是在每次查找时,令查找路径上的每个节点都直接指向根节点
int find_set(int node){
while(father[node] != node){
node = father[node];
}
return node;
}
//并查集的合并操作,将两个不相交的集合合并成一个,即将两棵不同的有根树
//通过小树的根节点指向大树的根节点,使得两棵有根树合并成合一课有根树
int _union(int p,int q){
int root1 = find_set(p);
int root2 = find_set(q);
if(root1==root2){
return 0; //如果当前操作到的两个节点同属于一个连通分量(即是同一棵树中的节点)
//则不执行合并操作直接返回0,表示合并失败
}
if(rank[root1] > rank[root2]){
father[root2] = root1; //小树连接到大树上,并且权值加至合并后
//整棵完整的树的树根上
rank[root1] += rank[root2];
}
else{
father[root1] = root2;
rank[root2] += rank[root1];
}
return 1;
}但是我们仔细想想,既然前面已经做了按秩合并的优化,那么是否这就是算法的最佳优化效果呢?
我们试着看一下这张图:
首先我们考虑,如果我们操作到的元素为a和b,那么a找到根节点需要的操作次数为(n-1)次,b找到根节点需要的操作次数为(n-2)次,
那么当节点数比较多的时候,寻找根节点的过程是可以再压缩的,我们可以这样想,a,b,c,d...乃至后面所有的节点(包括根节点),在执行查询的过程中,都是为了找到自己所属的这个集合中的代表元素(也就是根节点),那么除了根节点以外的节点,在这个时候是没有主次之分,也没有像二叉树那样严格区分左右子树的行为,所以呢,我们为了提高查找根节点的效率,我们可以简化查询操作,将根节点以外的所有节点都直接接在根节点的后面,这样的话能将查找的时间均摊,并且使得算法的效率接近常数级。
这种操作我们叫做路径压缩操作,具体实现我们可以在查找的过程中,便查找边压缩,如果待操作节点不是根节点,那么就将其接至根节点的后面。我们可以用递归操作(注意栈溢出的问题)和非递归操作实现:
递归操作:
int find_set(int node) {
if (father[node] != node) {
father[node] = find_set(father[node]); //在 find_set 函数中,当前结点不是根结点的情况下,
//将递归的结果赋值为当前结点的父节点,而递归结束的条件是
} //找到根节点,即if循环不成立的时候,递归结束,返回根节点至上一层调用该
return father[node]; //函数的地方,然后将上一层函数节点的父亲节点赋值为根节点
//随后重复上述操作,将"父亲节点(根节点)"带回上一层函数并赋值,直到最外层调用递归的函数
//该函数将"父亲节点(根节点)"返回至_union函数
}非递归操作(我们要先找到根节点,并将途经的节点一一保存起来,然后再重新遍历一次将途经节点的父节点均赋值为根节点):
/* 非递归方法,使用迭代的方式寻找根节点
* 需遍历两次节点(重复操作较多)
*/
int find_set(int node)
{
//如果是直接孩子或树根,则直接返回树根
if (father[node] == node)
return father[node];
int rec[size], root, k = 0;
//退出循环时即找到了树根i,因为此时father[i] == i;
//查找路径上的结点已经保存到rec数组,树根保存为root
for (; father[node] != node; node = father[node])
rec[k++] = node;
root = node; //根节点
//数组中的元素其父亲全部设置为root
int i = 0;
for (; i != k; i++)
father[rec[i]] = root;
return root;
}因此经过以上 按秩合并操作和路径压缩优化后,则实现的完整代码如下(C语言实现):
#include<stdio.h>
#define size 101
int father[size],rank[size];
//并查集初始化操作
void Init(int N){
int i;
for(i = 1;i < N;++i){
father[i] = i;
rank[i] = 1; //father[i]用于记录节点i的父亲节点,而rank[i]则用于记录
//节点i作为根节点时整棵树的大小(也称权重,用于记录树的节点个数)
}
}
//并查集的查询操作,查询当前操作到的节点的根节点
//在查询操作中,我们需要将查询的过程压缩,即减少向上遍历询问次数
//那么一般情况下会采取路径压缩的做法
//路径压缩:就是在每次查找时,令查找路径上的每个节点都直接指向根节点
int find_set(int node) {
if (father[node] != node) {
father[node] = find_set(father[node]); //在 find_set 函数中,当前结点不是根结点的情况下,
//将递归的结果赋值为当前结点的父节点,而递归结束的条件是
} //找到根节点,即if循环不成立的时候,递归结束,返回根节点至上一层调用该
return father[node]; //函数的地方,然后将上一层函数节点的父亲节点赋值为根节点
//随后重复上述操作,将"父亲节点(根节点)"带回上一层函数并赋值,直到最外层调用递归的函数
//该函数将"父亲节点(根节点)"返回至_union函数
}
//并查集的合并操作,将两个不相交的集合合并成一个,即将两棵不同的有根树
//通过小树的根节点指向大树的根节点,使得两棵有根树合并成合一课有根树
int _union(int p,int q){
int root1 = find_set(p);
int root2 = find_set(q);
if(root1==root2){
return 0; //如果当前操作到的两个节点同属于一个连通分量(即是同一棵树中的节点)
//则不执行合并操作直接返回0,表示合并失败
}
if(rank[root1] > rank[root2]){
father[root2] = root1; //小树连接到大树上,并且权值加至合并后
//整棵完整的树的树根上
rank[root1] += rank[root2];
}
else{
father[root1] = root2;
rank[root2] += rank[root1];
}
return 1;
}
int main(){
int i, m, x, y;
Init(size); //初始化操作
scanf("%d",&m); //m表示操作次数
for (i = 0; i < m; ++i) {
scanf("%d %d",&x,&y);
int ans = _union(x, y);
if (ans) {
printf("success\n");
}
else {
printf("failed\n");
}
}
return 0;
}
#include <iostream>
#include<algorithm>
using namespace std;
class DisjointSet {
private:
int *father, *rank;
public:
DisjointSet(int size) {
father = new int[size];
rank = new int[size];
for (int i = 0; i < size; ++i) {
father[i] = i;
rank[i] = 0;
}
}
~DisjointSet() {
delete[] father;
delete[] rank;
}
int find_set(int node) {
if (father[node] != node) {
father[node] = find_set(father[node]);
}
return father[node];
}
bool merge(int node1, int node2) {
int ancestor1 = find_set(node1);
int ancestor2 = find_set(node2);
if (ancestor1 != ancestor2) {
if (rank[ancestor1] > rank[ancestor2]) {
swap(ancestor1, ancestor2);
}
father[ancestor1] = ancestor2;
rank[ancestor2] = max(rank[ancestor1] + 1, rank[ancestor2]);
return true;
}
return false;
}
};
int main() {
DisjointSet dsu(100);
int m, x, y;
cin >> m;
for (int i = 0; i < m; ++i) {
cin >> x >> y;
bool ans = dsu.merge(x, y);
if (ans) {
cout << "success" << endl;
} else {
cout << "failed" << endl;
}
}
return 0;
}
总结:并查集算法涉及到很多算法优化的思想,需要多练习熟悉,并且要深入理解并查集算法。
除了学校oj外,另外还有一些并查集的题目可以试着做一做:
poj 2542 poj1182(较难,可仔细琢磨)
POJ 1308 1456 1611 1703 1733 1984 1986(LCA Tarjan算法 + 并查集) 1988 2236 2492 2524。
HDU 3038
如有错误,还请指正,O(∩_∩)O谢谢


























 846
846











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








