【迷之模拟赛】魔法水晶

最新推荐文章于 2020-08-20 16:06:09 发布

LOI_xczhw

最新推荐文章于 2020-08-20 16:06:09 发布

阅读量1.1k

点赞数 1

分类专栏： lca =====小算法===== 倍增

本文链接：https://blog.csdn.net/LOI_xczhw/article/details/49454831

版权

=====小算法===== 同时被 3 个专栏收录

27 篇文章 0 订阅

订阅专栏

lca

1 篇文章 0 订阅

订阅专栏

倍增

1 篇文章 0 订阅

订阅专栏

这套神秘的题目来自神秘的人，神秘的一套题让我被神秘的虐了半天……

题目描述

魔法水晶承载着魔法师的法力，是魔法师法力的结晶。
Elsa 拥有 n 个魔法水晶。为了让这 n 个魔法水晶处于相互联系的状态中，
并且不出现流动混乱，Elsa 用 n-1 条法力流动通道将魔法水晶联系起来。每条
通道直接连接两个魔法水晶，并且每对魔法水晶都直接或间接相连。
每条法力流动通道有一个延迟量，一对魔法水晶之间的延迟量是连接它们
的路径上所有通道的延迟量之和。n 个魔法水晶这一整体的总延迟是每对魔法
水晶之间的延迟量的和。
Elsa 会进行 m 次施法操作，每次施法会将连接魔法水晶 u 和 v 的路径上所
有的法力流动通道的延迟量增加 w。
她需要你帮助她动态地计算 n 个魔法水晶这一整体的总延迟。

输入格式

第一行一个数 n，接下来 n-1 行，每行三个数 a、b、c，表示有一条连接
a、b 的延迟量为 c 的法力流动通道。
接下来一个数 m，表示施法次数。接下来 m 行，每行三个数 u、v、w，表示
连接 u 和 v 的路径上的每一条法力流动通道的延迟量都增加 w。

输出格式

输出 m+1 行，第 i 行输出一个整数表示完成前(i-1)次施法操作后的总延
迟。
答案对 1,000,000,007 取模。

样例输入

3
1 2 2
1 3 1
2
1 2 -2
2 3 1

样例输出

6
2
6

数据范围

20%的数据，n,m≤50
40%的数据，n,m≤300
60%的数据，n,m≤3000
另 20%的数据，m=0
100%的数据，n,m≤100000，-10^9≤c,w≤10^9

作为压轴题目……感觉质量 += INF……
总结下题意的话，就是给你一棵树，然后求这个东西
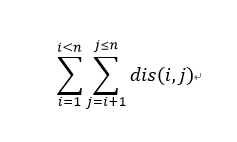
这里写图片描述
//定义dis(i,j)为i到j上路径的权值和
并且支持修改，使(u,v)上的所有的边权值 += v;
暴力比较好想……显而易见的有模拟+lca
修改暴力修改
n^2暴力求和
这样的话是n^3的……
显然这样是不行的，于是我们就想着怎么去优化
比较容易想到的是对边下手，能不能快速的求出一条边对于答案的贡献呢？
我们先考虑一条链上的情况
这里写图片描述
比如这张图，我们考虑每一条边上的情况，对于边(1,2)，在计算dis(1,2),dis(1,3),dis(1,4),dis(1,5)的时候各被计算了一次，那么对于边(2,3),计算的时候分别是在dis(1,3),dis(1,4),dis(1,5)和dis(2,3),dis(2,4),dis(2,5)，换句话说，一条边对答案的贡献就是(左边的点数*右边的点数)……
那么，在树上也是相同的，乘起来就行了嗯……~~这不就是乘法原理么~~
所以，我们需要快速的调取一条边两边的点的个数，可以在dfs的时候记录子树的size
那么我们来看一棵树，圈里的是点编号，括号里的是size
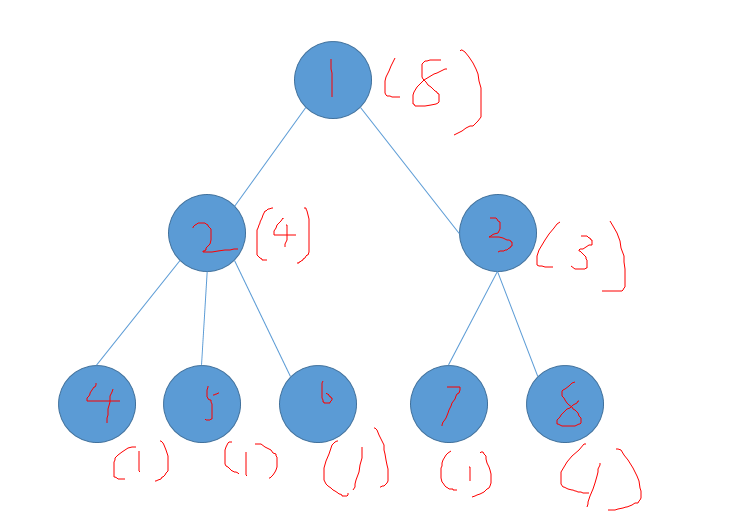
这里写图片描述
如果想看边(1,2)被计算的次数，显然不是简单地sz[1] * sz[2]
2的sz是真实的，1的不是……
也就是说，deep大的那个节点的sz是真实的，另一个可以用n - sz[]来求得
也就是

ll ci(ll x,ll y)
{
    if(deep[x] < deep[y])
        swap(x,y);
    return sz[x] * (n - sz[x]);
}

显然，一条边连接的两点deep不会相等……
那么就可以分析答案了
答案一共m + 1行，对于第一行的输出，我们可以通过枚举m条边，然后用上面的ci来算，第一次的ans解决！
然后，修改
怎么办呢
容易发现，其实没必要真的修改边权，我只需要在之前的ans上操作就好
可以想到在dis(u,v)上操作，在这条路径上的边，我们如果可以知道一条边被计算几次的话，不就可以直接知道答案了么
恩恩
怎么搞呢
还记得小机房的树么？没错，我们同样可以记录
两种方法，一个是因为他满足区间加法，另一个是因为他满足区间减法，我比较推荐后面那一种，好写，好理解

先说第一种方法，在倍增lca的时候，我们可以顺带记录一个sum[i][j]表示i往上蹦1 << j步的这个过程上的边一共需要计算多少次，然后无脑加就好

另一种，我们可以简单的记录root[i]表示从i到根的路径上的边共被记录多少次，在修改(u,v)时候，ans就+= (root[u] + root[v] - (root[lca(u,v)] << 1)) * v即可

嗯，就是这样
那么就解决了，顺带一提，这题因为乘法，数据会比较大，别忘了longlong，别忘了取模！！！！

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define KILL puts("haha");
using namespace std;
typedef long long ll;
const ll MAXN = 100000 + 5;
const ll MAXM = 100000 + 5;
const ll P = 1e9 + 7;
struct edge
{
    ll f,t,v;
}l[MAXM << 1];
ll first[MAXN],next[MAXM << 1],tot;
ll n;
void init()
{
    memset(first,0xfff,sizeof(first));
    tot = 0;
    return;
}
void build(ll f,ll t,ll v)
{
    l[++tot] = (edge){f,t,v};
    next[tot] = first[f];
    first[f] = tot;
    return;
}
ll fa[MAXN][35],deep[MAXN];
void get_fa()
{
    for(int j = 1;j <= 30;j ++)
        for(int i = 1;i <= n;i ++)
            fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
ll lca(ll x,ll y)
{
    if(deep[x] < deep[y])
        swap(x,y);
    for(int j = 30;j >= 0;j --)
        if(deep[fa[x][j]] >= deep[y])
            x = fa[x][j];
    if(x == y)
        return x;
    for(int j = 30;j >= 0;j --)
        if(fa[x][j] != fa[y][j])
            x = fa[x][j],y = fa[y][j];
    return fa[x][0];
}
ll sz[MAXN];
void dfs(ll x,ll f)
{
    fa[x][0] = f;
    sz[x] = 1;
    deep[x] = deep[f] + 1;
    for(int i = first[x];~i;i = next[i])
        if(l[i].t != f)
        {
            dfs(l[i].t,x);
            sz[x] += sz[l[i].t];
        }
    return;
}
ll root[MAXN];
ll ci(ll x,ll y)
{
    if(deep[x] < deep[y])
        swap(x,y);
    return sz[x] * (n - sz[x]);
}
void dfs(ll x)
{
    root[x] = root[fa[x][0]] + ci(fa[x][0],x);
    for(int i = first[x];~i;i = next[i])
        if(l[i].t != fa[x][0])
            dfs(l[i].t);
    return;
}
ll ans = 0;
void solve()
{
    for(int i = 1;i <= tot;i += 2)
        ans += (ci(l[i].f,l[i].t) % P * l[i].v % P) % P,ans %= P;
    ans %= P;
    return;
}
ll m;
ll f,t,v;
int main()
{
    freopen("sum.in","r",stdin);
    freopen("sum.out","w",stdout);
    init();
    scanf("%lld",&n);
    for(int i = 1;i < n;i ++)
    {
        scanf("%lld %lld %lld",&f,&t,&v);
        while(v < 0)
            v += P;
        v %= P;
        build(f,t,v);
        build(t,f,v);
    }
    dfs(1,0);
    get_fa();
    dfs(1);
    solve();
    printf("%lld\n",ans);
    scanf("%lld",&m);
    for(int i = 1;i <= m;i ++)
    {
        scanf("%lld %lld %lld",&f,&t,&v);
        while(v < 0)
            v += P;
        v %= P;
        ans = ((ans % P + (root[f] % P + root[t] % P - ((root[lca(f,t)] % P) << 1) % P) % P * (v % P)) % P) % P;
        while(ans < 0)
            ans += P;
        printf("%lld\n",ans % P);
        ans %= P;
    }
    return 0;
}