[胡策题] 魔法水晶树上问题~(四星)

最新推荐文章于 2020-03-26 18:21:47 发布

ZJM__

最新推荐文章于 2020-03-26 18:21:47 发布

阅读量854

点赞数 1

分类专栏： ------不务正业系列------ ------NOIP------ 文章标签： lca 倍增树树上问题

本文链接：https://blog.csdn.net/Loi_Seavot/article/details/49446859

版权

------不务正业系列------ 同时被 2 个专栏收录

21 篇文章 0 订阅

订阅专栏

------NOIP------

8 篇文章 0 订阅

订阅专栏

由于题目是从外校弄来的……于是只有数据和题面~这里我会放上题面，如果有想要数据的可以留言~

                                                    魔法水晶

【题目描述】

魔法水晶承载着魔法师的法力，是魔法师法力的结晶。
Elsa 拥有 n 个魔法水晶。为了让这 n 个魔法水晶处于相互联系的状态中，
并且不出现流动混乱，Elsa 用 n-1 条法力流动通道将魔法水晶联系起来。每条
通道直接连接两个魔法水晶，并且每对魔法水晶都直接或间接相连。
每条法力流动通道有一个延迟量，一对魔法水晶之间的延迟量是连接它们
的路径上所有通道的延迟量之和。n 个魔法水晶这一整体的总延迟是每对魔法
水晶之间的延迟量的和。
Elsa 会进行 m 次施法操作，每次施法会将连接魔法水晶 u 和 v 的路径上所
有的法力流动通道的延迟量增加 w。
她需要你帮助她动态地计算 n 个魔法水晶这一整体的总延迟。

【输入格式】

第一行一个数 n，接下来 n-1 行，每行三个数 a、b、c，表示有一条连接
a、b 的延迟量为 c 的法力流动通道。
接下来一个数 m，表示施法次数。接下来 m 行，每行三个数 u、v、w，表示
连接 u 和 v 的路径上的每一条法力流动通道的延迟量都增加 w。

【输出格式】

输出 m+1 行，第 i 行输出一个整数表示完成前(i-1)次施法操作后的总延
迟。
答案对 1,000,000,007 取模。

【样例输入】

3
1 2 2
1 3 1
2
1 2 -2
2 3 1

【样例输出】

6
2
6

【数据规模与约定】

20%的数据，n,m≤50
40%的数据，n,m≤300
60%的数据，n,m≤3000
另 20%的数据，m=0
100%的数据，n,m≤100000，-10^9≤c,w≤10^9

题解：

看到这个题的时候，如果不看数据范围那就是暴力lca，每次修改该边的边权。然后暴力求和，这样乱搞一下应该可以拿到80分……（因为60的算法是n^2,有20% m == 0）

然后我们来想一下，树上问题一般可以转成树链剖分，这个题有区间修改，是不是也能转化成树链剖分呢？
我们继续想，把树链剖出来，区间修改是解决了，每次修改区间，但是每次修改后要查询全部和，这样树链剖分的复杂度还是比较高的，全局来说就是（n^2 * logn）的复杂度，对于100%的复杂度还是不行，那么我们需要转化一下思路了，NOIP级别的思路（这是NOIP模拟题）：

每次求取全部的边这个复杂度很高，我们着手从这个地方优化。一个边对答案的贡献就是每次用到这个边的时候加一次，那么是不是可以与处理一下一个边在一次询问时应该加几次呢？答案是显然的！
我们用一个dfs统计一下每个点的深度，那么一条边对答案的影响就是深度较大的点的子树大小*(n-深度较大的子树大小)，这里很容易想，我还是放一张图来帮助理解：
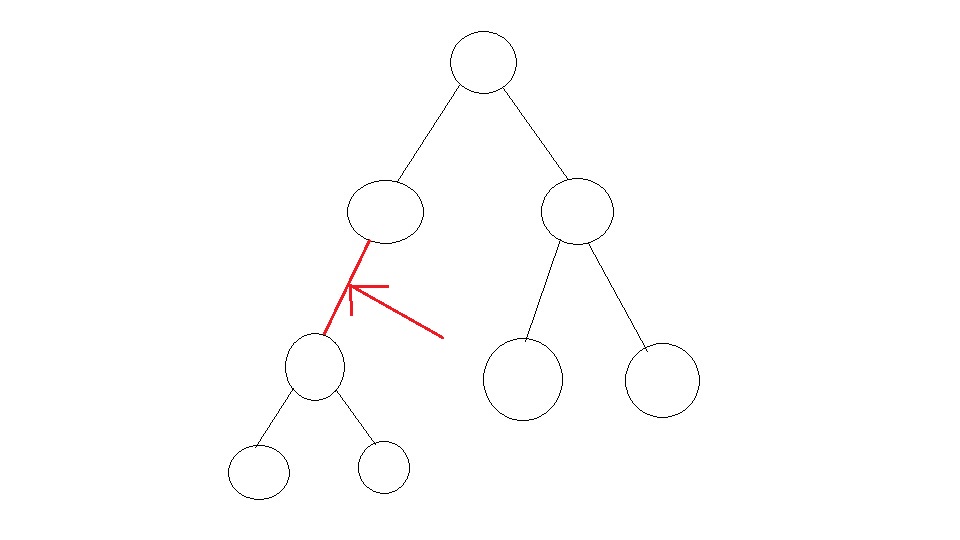
这里写图片描述
对于图中的边，他对答案的影响就是（dist*3（子树大小）*5(n-子树大小~)）；
因为左边的点往右边跑无论如何都得跑这条边，根据乘法原理，就能得出这个结论~

那这一步我们就优化到了o(n)的复杂度，但是，对于每次询问都用ON最终复杂度就是n*m，类似n^2，还是不行，我们再优化：

这个题目仔细想一下有个性质：如果第一次求得了初始答案，之后每次操作时都是将路径上的边权加一个固定的值，如果稍微转化一下就是将上一次的答案加上路径上边需要加的总次数乘上当前的要加的值。这个转化很微妙，经过转化后，每次操作只需要快速求的路径上边要加的总次数即可，而快速求总次数就可以用倍增LCA来处理，s[i][j]表示i点往上跳j次的边的总次数，这样就把查询优化到了log级别，配合100%的数据范围也能过了~

做这个题需要注意的就是取模了，在 + - * 的运算中取模多了不会出事少了说不定就爆了，另外也不要作死开int因为数据很大很大很大……中间过程就爆了………………，在对答案有影响的所有地方都加取模，保证每一步都在mod范围以内，另外还有负数的情况，这种情况需要(ans + mod )%mod就能把答案变成正数了~
付代码一份：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<stack>
#include<map>
#include<cmath>
using namespace std;
typedef long long ll;
const ll mod = 1000000007;
const int size = 500010;
map <int,map<int,int> > maps;
struct Edge{int from,to,dist;ll cnt;}edges[size];
int head[size],next[size],tot;
void build(int f,int t,int d)
{
    edges[++tot].to = t;
    edges[tot].from = f;
    edges[tot].dist = d;
    next[tot] = head[f];
    maps[f][t] = tot;
    head[f] = tot;
}
int n,deep[size],f[size][32];
ll s[size][32],siz[size];
void dfs(int u,int d)
{
    deep[u] = d,siz[u] = 1;
    for(int i = head[u];i;i = next[i])
    {
        int v = edges[i].to;
        if(!deep[v])
        {
            f[v][0] = u;
            dfs(v,d+1);
            siz[u] += siz[v];
        }
    }
}
void init()
{
    int k = (int)(log2(n))+1;
    for(int j = 1;j <= k;j ++)
    {
        for(int i = 1;i <= n;i ++)
        {
            f[i][j] = f[f[i][j-1]][j-1];
            s[i][j] = (s[f[i][j-1]][j-1]%mod+s[i][j-1]%mod)%mod;
        }
    }
}
ll ans;
int find(int a,int b)
{
    int k = (int)(log2(n)) + 1;
    ll cntt = 0;
    if(deep[a] > deep[b])   swap(a,b);
    for(int i = k;i >= 0;i --)
    {
        if(deep[f[b][i]] < deep[a]) continue;
        cntt =(cntt%mod + s[b][i]%mod)%mod;
        b = f[b][i];
    }
    for(int i = k;i >= 0;i --)
    {
        if(f[a][i] == f[b][i])  continue;
        cntt = (cntt%mod + s[a][i]%mod)%mod;
        cntt = (cntt%mod + s[b][i]%mod)%mod;
        a = f[a][i];
        b = f[b][i];
    }
    if(a != b)
    {
        cntt = (cntt%mod + s[a][0]%mod)%mod;
        cntt = (cntt%mod + s[b][0]%mod)%mod;
    }
    return cntt;
}
int main()
{
    scanf("%d",&n);
    for(int i = 1;i < n;i ++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        build(a,b,c);
        build(b,a,c);
    }
    dfs(1,1);
    for(int i = 1;i <= tot;i ++)
    {
        bool flag = 0;
        int f = edges[i].from;
        int t = edges[i].to;
        if(deep[f] > deep[t])   swap(f,t);
        ll cishu = ((ll)(siz[t])%mod)*((ll)(n-siz[t])%mod)%mod;
//        cout<<cishu<<endl;
        edges[maps[f][t]].cnt = cishu;
        s[t][0] = cishu;
    }
    init();
    for(int i = 1;i <= tot;i ++)  ans = (ans%mod + (((ll)(edges[i].dist)%mod)*(edges[i].cnt%mod))%mod)%mod;
    if(ans < 0) ans = (ans + mod)%mod;
    printf("%lld\n",ans);
    int q;
    scanf("%d",&q);
    while(q--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        ll tmp = find(a,b);
        ans = (ans%mod + (tmp*((ll)(c)%mod))%mod)%mod;
        if(ans < 0) ans = (ans + mod)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}