C++线段树初步（上）

先给大家举个栗子

//本例题摘自
https://wenku.baidu.com/view/b9e84029a66e58fafab069dc5022aaea998f4116.html
描述
　　老管家是一个聪明能干的人。他为财主工作了整整10年，财主为了让自已账目更加清楚。要求管家每天记k次账，由于管家聪明能干，因而管家总是让财主十分满意。但是由于一些人的挑拨，财主还是对管家产生了怀疑。于是他决定用一种特别的方法来判断管家的忠诚，他把每次的账目按1，2，3…编号，然后不定时的问管家问题，问题是这样的：在a到b号账中最少的一笔是多少？为了让管家没时间作假他总是一次问多个问题。
　　在询问过程中账本的内容可能会被修改。
　　
　　输入格式:
　　输入中第一行有两个数m,n表示有m(m<=100000)笔账,n表示有n个问题，n<=100000。
　　接下来每行为3个数字，第一个p为数字1或数字2，第二个数为x，第三个数为y。
　当p=1 则查询x,y区间。
　当p=2 则改变第x个数为y。
——————————————————————————————
　　相信很多初学者看到这道题第一反应都是用数组模拟。但是请注意数据规模为100000。若直接存入一维数组中再依次计算x-y的区间和无疑会TLE。若一开始使用前缀和相加的形式，中途一旦改变某个数据的值，剩下所有保留的前缀和都需要更改。因此我们需要找到一种更加高效的查找、修改方法来快速找到该值。
　　
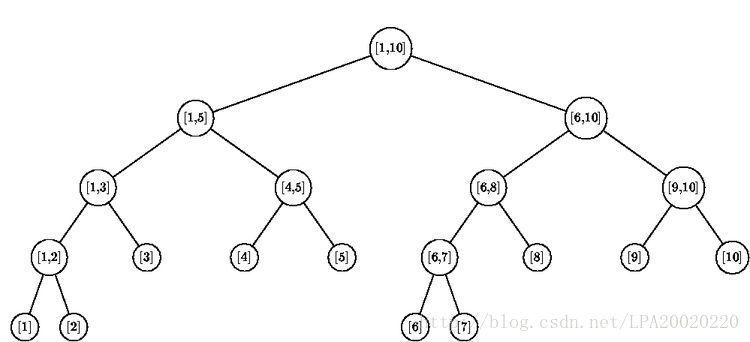
　　如上图，线段树是一种集索引和数据本身为一体的数据结构。其采用了二分思想，修改和计算的步骤都继承了其时间复杂度为O（logN）的优点，显然可以满足该题要求。
　　那么，我们该如何构建一棵线段树呢？
　　显然，线段树为一颗二叉树，则设其父节点为tree[n]，子节点为tree[2*n]与tree[2*n+1]。因此我们可以用数组进行构造操作，其下标可以连通子节点与父节点。

注：下列代码片以寻找区间最大值与和为目的（博主很懒懒得改源程序(｀・ω・´)），并非为例题标准源程序。

struct sd
{
    int left;//当前集合左结点
    int right;//右结点
    int sum;//当前和
    int maxx;//当前最大值
    sd()
    {
        memset(this,0,sizeof(this));//初始化值
    }
};
sd tree[500000];

又：网上各种大犇有介绍其他构造方法的，博主（蒟蒻）不予介绍(TAT)。
不过可以不开结构体，另开几个数组存储…
注：数组一定要开的够大（4*N）以防超界RE！

　　接下来开始构造线段树，博主用递归构造，但好像也可以用递推。
　　

void updata(int n)//更新父节点的初值
{
    tree[n].maxx=max(tree[n*2].maxx,tree[n*2+1].maxx);
    tree[n].sum=tree[n*2].sum+tree[n*2+1].sum;
}
void build_tree(int t,int lef,int rig)
//分别代表对应tree数组中下标，区间左结点，右结点
//默认应由1开始，1为左结点，数据范围为右结点
{
    tree[t].left=lef;//保存当前区间
    tree[t].right=rig;
    if(lef==rig)//若为最底层节点则从数组中读入数据，博主事先保存在了pre中
    {
        tree[t].sum=pre[lef];
        tree[t].maxx=pre[lef];
        return;
    }
    int mid=(lef+rig)/2 ;//二分递归构造
    build_tree(t*2,lef,mid);
    build_tree(t*2+1,mid+1,rig);
    updata(t);
}

　　若题目没有输入初值，则此步骤不需要updata。
　　可使用移位运算符加速*2与*2+1，具体请参考百度百科“移位运算符”词条。
　　此步骤完成后线段树上都拥有了初值，接下来就开始进行求和和求最大值的步骤。
　　

int inquiry_sum(int t,int lef,int rig)
{
    if(lef==tree[t].left&&rig==tree[t].right)//正好为查找的区间
    {
        return tree[t].sum;
    }
    int mid=(tree[t].left+tree[t].right)/2;//二分
    if(mid>=rig)  return inquiry_sum(t*2,lef,rig);
    //说明查找区间只在当前区间的左半区间范围内
    //注意此处不能改变lef和rig的值，博主找了半天bug才发现...
    else if(mid<lef)  return inquiry_sum(t*2+1,lef,rig);
    ///说明查找区间只在当前区间的右半区间范围内
    else 
return inquiry_sum(t*2,lef,mid)+inquiry_sum(t*2+1,mid+1,rig); 
//否则为跨区间，在两边搜索
} 

此处应该注意的是*2与*2+1的对应关系，与前面构造的时候应保证一致。
最大值查找方式也差不多，贴上函数：

int inquiry_max(int t,int lef,int rig)
{
    if(lef==tree[t].left&&rig==tree[t].right)
    {
        return tree[t].maxx;
    }
    int mid=(tree[t].left+tree[t].right)/2;
    if(mid>=rig)return inquiry_max(t*2,lef,rig);
    else if(mid<lef)return inquiry_max(t*2+1,lef,rig);
    else return max(inquiry_max(t*2,lef,mid),inquiry_max(t*2+1,mid+1,rig));
}

（博主有变量和函数都定成英文的习惯，所以代码格外长..(｡･ω･｡)）
接下来就是改数据的操作了，同样递归完成。

void change(int now,int tar,int delta)
//对应当前查找的数组下标，目标的位置，以及改变后的数据
{
    if(tree[now].left ==tar&&tree[now].right==tar)//找到改点则修改
    {
        tree[now].sum=delta;
        tree[now].maxx=delta;
        return;
    }
    int mid=(tree[now].left+tree[now].right)/2;//否则二分查找
    if(tar<=mid)change(2*now,tar,delta);//左半区
    else change(2*now+1,tar,delta);//右半区
    updata(now);//完成后修改父节点
}

修改数据的方式可以自己写，依题目而定。
最后贴上博主的（辣鸡）代码

#include<bits/stdc++.h>
using namespace std;
struct sd
{
    int left;int right;int sum;int maxx;
    sd()
    {
        memset(this,0,sizeof(this));
    }
};
sd tree[100005];
int pre[10005];
void updata(int n)
{
    tree[n].maxx=max(tree[n*2].maxx,tree[n*2+1].maxx);
    tree[n].sum=tree[n*2].sum+tree[n*2+1].sum;
}
void build_tree(int t,int lef,int rig)
{
    tree[t].left=lef;
    tree[t].right=rig;
    if(lef==rig)
    {
        tree[t].sum=pre[lef];
        tree[t].maxx=pre[lef];
        return;
    }
    int mid=(lef+rig)/2 ;
    build_tree(t*2,lef,mid);
    build_tree(t*2+1,mid+1,rig);
    updata(t);
}
int inquiry_sum(int t,int lef,int rig)
{
    if(lef==tree[t].left&&rig==tree[t].right)
    {
        return tree[t].sum;
    }
    int mid=(tree[t].left+tree[t].right)/2;
    if(mid>=rig)return inquiry_sum(t*2,lef,rig);
    else if(mid<lef)return inquiry_sum(t*2+1,lef,rig);
    else return inquiry_sum(t*2,lef,mid)+inquiry_sum(t*2+1,mid+1,rig); 
} 
int inquiry_max(int t,int lef,int rig)
{
    if(lef==tree[t].left&&rig==tree[t].right)
    {
        return tree[t].maxx;
    }
    int mid=(tree[t].left+tree[t].right)/2;
    if(mid>=rig)return inquiry_max(t*2,lef,rig);
    else if(mid<lef)return inquiry_max(t*2+1,lef,rig);
    else return max(inquiry_max(t*2,lef,mid),inquiry_max(t*2+1,mid+1,rig));
}
void change(int now,int tar,int delta)
{
    if(tree[now].left ==tar&&tree[now].right==tar)
    {
        tree[now].sum=delta;
        tree[now].maxx=delta;
        return;
    }
    int mid=(tree[now].left+tree[now].right)/2;
    if(tar<=mid)change(2*now,tar,delta);
    else change(2*now+1,tar,delta);
    updata(now);
}
void add(int now,int tar,int delta)
{
    if(tree[now].left ==tar&&tree[now].right==tar)
    {
        tree[now].sum+=delta;
        tree[now].maxx+=delta;
        return;
    }
    int mid=(tree[now].left+tree[now].right)/2;
    if(tar<=mid)add(2*now,tar,delta);
    else add(2*now+1,tar,delta);
    updata(now);
}
int main()
{
    printf("请输入数据个数\n");
    int num;
    scanf("%d",&num);
    printf("请依次输入数据\n");
    for(int i=1;i<=num;i++)
    {
        scanf("%d",&pre[i]);
    } 
    build_tree(1,1,num);
    int a,b,c;
    printf("操作开始\n");
    printf("Tips:输入格式\n");
    printf("1,x,y-->输出第x个至第y个数据的和\n");
    printf("2,x,y-->输出第x个至第y个数据的最大值\n");
    printf("3,x,y-->将第x个数据改为y\n");
    printf("4,x,y-->将第x个数据加上y\n");
    printf("若要退出程序，输入3个0\n");
    while (true)
    {
    scanf("%d%d%d",&a,&b,&c);
    if(a==0)break;
    if(a==1)printf("操作结果：%d\n",inquiry_sum(1,b,c));
    if(a==2)printf("操作结果：%d\n",inquiry_max(1,b,c));
    if(a==3)
    {
        change(1,b,c);
        printf("操作完成！\n");
    }
    if(a==4)
    {
         add(1,b,c);
         printf("操作完成！\n");
    }
    }
    printf("感谢使用！\n");
    return 0;
}

本次分享就到这里了。不过显然在实际操作中还有不少问题，例如想要使一个区间中所有数据都改变，若一个一个地查找就非常慢了，达到了N(logN)的时间复杂度，优化方法将会在下期揭晓。我们下期再见。