【2010集训队】书堆

Description

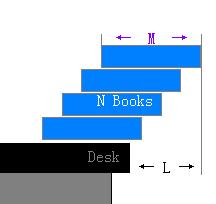
蚂蚁是勤劳的动物，他们喜欢挑战极限。现在他们迎来了一个难题！蚂蚁居住在图书馆里，图书馆里有大量的书籍。书是形状大小质量都一样的矩形。蚂蚁要把这些书摆在水平桌子的边缘。蚂蚁喜欢整洁的布置，所以蚂蚁规定书本必须水平摆放，宽必须平行于桌缘（如图），而且不允许同一高度摆多本书。

蚂蚁想要让书本伸出桌子边缘尽量远，同时不让书因为重力垮下来。它们已经用不知道什么方法测出了书的长度M（如图）。如果总共有N本书，请你帮忙计算如何摆放使得最多水平伸出桌缘多远。你不用考虑蚂蚁用什么方法搭建这堆书。

如果某本书以上的所有书的重心的竖直射影不在这本书上，或者正好落在在这本书的边界上，那么这堆书是不稳定的，会因为重力而垮下来。

• 不考虑地球自转，重力系数也不因高度改变；

• 书是质量均匀，质地坚硬的理想二维物体；

• 在不会垮的前提下，每本书的位置坐标可以是任意实数。

Solution

先假定书的重心可以到达书本的边界。

思考一下，对于 $i$ 以上的书本来说，最优情况就是重心落在 $i$ 的最右端。

不妨设桌面最右边为 0，书本自下而上编号 $1\sim n$，重心的 $x$ 坐标为 $g_i$。

那么根据重心位置公式可得

$\{\begin{array}{l}0=\frac{\sum _{i=1}^n{g}_i}{n}\\ g_1+\frac{1}{2}=\frac{\sum _{i=2}^n{g}_i}{n-1}\\ \dots \end{array}$

解得

$\{\begin{array}{l}{g}_1=\frac{1}{2n}-\frac{1}{2}\\ g_2=\frac{1}{2(n-1)}+g_1\\ \dots \\ g_n=\frac{1}{2}+g_{n-1}\end{array}$

那么 $ans=m\times (g_n+\frac{1}{2})=m\times (\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\dots )=m\times \sum _{i=1}^n\frac{1}{2i}$。

这个式子在 $n\le 10^{18}$ 的情况下肯定是没有办法线性求出的。所以回想一下数学上的一些知识。

$\sum _{i=1}^n\frac{1}{i}$ 这个式子称为调和级数，而调和级数有公式：$\gamma ={\lim }_{n\to \infty }\left({\sum }_{k=1}^{\infty }\frac{1}{k}-\ln n\right)$。$\gamma$ 是欧拉常数，$\gamma \approx 0.577215664901532$。当 $n\ge 10^7$ 的时候，误差已经减小到不会影响整数位了，所以可以直接 $\mathcal{O}(1)$ 得到结果。

此时为了满足题意：不能落在边界上，可以将答案先减去一个较小的数（例如 $10^{-7}$）后再取整。但注意这个数不能太小，也不能太大。

Code

#include<cmath>
#include<cstdio>
#define gama 0.577215664901
#define eps 1e-7
using namespace std;
long long n,m,ans;
double sum;
int main()
{
    scanf("%lld%lld",&n,&m);
    if (n>=10000000) sum=(log(n)+gama)/2.0;
    else
    {
        for (int i=2;i<=2*n;i+=2)
            sum+=(1.0/i);
    }
    ans=m*sum-eps;
    printf("%lld\n",ans);
    return 0;
}