降维算法（PCA）

最新推荐文章于 2024-04-26 11:34:55 发布
最新推荐文章于 2024-04-26 11:34:55 发布
阅读量1.4w 收藏 25
点赞数 3
分类专栏： 机器学习 算法 文章标签： 算法 数据清洗
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/LanboCSDN/article/details/78391375
版权

降维方法

1、主成分分析（PCA）
在PCA中，数据从原来的坐标系转换到新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复，重复次数为原始数据中特征的数目。我们会发现，大部分方差都包含在最前面的几个新坐标轴中。因此，我们可以忽略余下的坐标轴，即对数据进行降维处理。

2、因子分析（Factor Analysis）。在因子分析中，我们假设在观察数据的生成中有一些观察不到的隐变量（latent variable）。假设观察数据是这些隐变量和某些噪声数据的线性组合。那么隐变量的数据可能比观察数据的数目少，也就是说通过找到隐变量就可以实现数据降维。

3、独立成分分析（ICA）
ICA假设数据从N个数据源生成的，和因子分析有些类似。假设数据为多个数据源的混合观察结果，这些数据源之间在统计上是相互独立的，而在PCA中只假设数据是不相关的。同因子分析一样，如果数据源的数目少于观察数据的数目，则可实现降维。

注：PCA应用最广泛，所以只介绍PCA。
线性判别分析（LDA）是一种经典的监督降维算法。主成分分析（PCA）是一种经典的无监督降维算法。

PCA降维的两个准则：
最近重构性：样本集中所有点，重构后的点距离原来的点的误差之和最小。
最大可分性：样本在低维空间的投影尽可能分开。

1、PCA
**scikit-learn中提供一个PCA类来实现PCA模型
decomposition.PCA( )**
注：decomposition.PCA不能应用于稀疏矩阵且无法适用于超大规模数据（因它要求所有的数据一次加载进内存）
参数
n_components：一个整数，指定降维后的维数
属性
explained_variance_ratio_：一个数组，元素是每个主成分explained variance的比例

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets,decomposition,manifold

def load_data():
    iris=datasets.load_iris()
    return iris.data,iris.target

def test_PCA(*data):
    X,y=data
    pca=decomposition.PCA(n_components=None)
    pca.fit(X)
    print('explained variance ratio : %s'%str(pca.explained_variance_ratio_))

X,y=load_data()
test_PCA(X,y)

def plot_PCA(*data):
    X,y=data
    pca=decomposition.PCA(n_components=2)
    pca.fit(X)
    X_r=pca.transform(X)

    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),(0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2))
    for label,color in zip(np.unique(y),colors):
        position=y==label
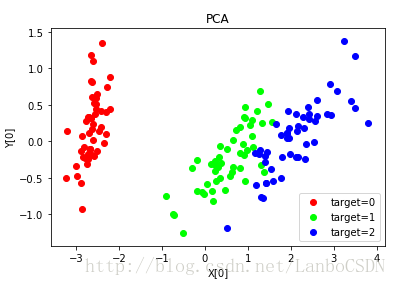
        ax.scatter(X_r[position,0],X_r[position,1],label="target=%d"%label,color=color)
    ax.set_xlabel("X[0]")
    ax.set_ylabel("Y[0]")
    ax.legend(loc="best")
    ax.set_title("PCA")
    plt.show()
plot_PCA(X,y)

这里写图片描述

2、超大规模数据降维IncrementalPCA
可以将数据分批加载进内存。

3、KernelPCA
decomposition.KernelPCA( )
参数
n_components：一个整数，指定降维后的维数，如果为None，则维数不变。
kernel：一个字符串，指定核函数
–linear：线性核
–poly：多项式核
–rbf：高斯核函数
–sigmoid
alpha：一个整数，岭回归的超参数，用于计算逆转矩阵（当fit_inverse_transform=True时）。inverse：逆，transform：转。先逆后转。
属性
lambdas_：核化矩阵的特征值
alphas_：核化矩阵的特征向量
dual_coef_：逆转换矩阵
方法
fit（X[ , y]）:训练模型
transform(X)：执行降维
fit_transform（X[ , y]）:训练模型并且降维
inverse_transform(X):执行升维，将数据从低维空间逆向转换到原始空间

import numpy as np
import matplotlib.pyplot as plt
from sklearn import   datasets,decomposition

def load_data():
    '''
    加载用于降维的数据
    :return: 一个元组，依次为训练样本集和样本集的标记
    '''
    iris=datasets.load_iris()# 使用 scikit-learn 自带的 iris 数据集
    return  iris.data,iris.target

def test_KPCA(*data):
    '''
    测试 KernelPCA 的用法
    :param data: 可变参数。它是一个元组，这里要求其元素依次为：训练样本集、训练样本的标记
    :return: None
    '''
    X,y=data
    kernels=['linear','poly','rbf','sigmoid']
    for kernel in kernels:
        kpca=decomposition.KernelPCA(n_components=None,kernel=kernel) # 依次测试四种核函数
        kpca.fit(X)
        print('kernel=%s --> lambdas: %s'% (kernel,kpca.lambdas_))
def plot_KPCA(*data):
    '''
    绘制经过 KernelPCA 降维到二维之后的样本点
    :param data: 可变参数。它是一个元组，这里要求其元素依次为：训练样本集、训练样本的标记
    :return: None
    '''
    X,y=data
    kernels=['linear','poly','rbf','sigmoid']
    fig=plt.figure()
    colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),
        (0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)# 颜色集合，不同标记的样本染不同的颜色

    for i,kernel in enumerate(kernels):
        kpca=decomposition.KernelPCA(n_components=2,kernel=kernel)
        kpca.fit(X)
        X_r=kpca.transform(X)# 原始数据集转换到二维
        ax=fig.add_subplot(2,2,i+1) ## 两行两列，每个单元显示一种核函数的 KernelPCA 的效果图
        for label ,color in zip( np.unique(y),colors):
            position=y==label
            ax.scatter(X_r[position,0],X_r[position,1],label="target= %d"%label,
            color=color)
        ax.set_xlabel("X[0]")
        ax.set_ylabel("X[1]")
        ax.legend(loc="best")
        ax.set_title("kernel=%s"%kernel)
    plt.suptitle("KPCA")
    plt.show()
def plot_KPCA_poly(*data):
    '''
    绘制经过 使用 poly 核的KernelPCA 降维到二维之后的样本点
    :param data: 可变参数。它是一个元组，这里要求其元素依次为：训练样本集、训练样本的标记
    :return: None
    '''
    X,y=data
    fig=plt.figure()
    colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),
        (0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)# 颜色集合，不同标记的样本染不同的颜色
    Params=[(3,1,1),(3,10,1),(3,1,10),(3,10,10),(10,1,1),(10,10,1),(10,1,10),(10,10,10)] # poly 核的参数组成的列表。
            # 每个元素是个元组，代表一组参数（依次为：p 值， gamma 值， r 值）
            # p 取值为：3，10
            # gamma 取值为 ：1，10
            # r 取值为：1，10
            # 排列组合一共 8 种组合
    for i,(p,gamma,r) in enumerate(Params):
        kpca=decomposition.KernelPCA(n_components=2,kernel='poly'
        ,gamma=gamma,degree=p,coef0=r)  # poly 核，目标为2维
        kpca.fit(X)
        X_r=kpca.transform(X)# 原始数据集转换到二维
        ax=fig.add_subplot(2,4,i+1)## 两行四列，每个单元显示核函数为 poly 的 KernelPCA 一组参数的效果图
        for label ,color in zip( np.unique(y),colors):
            position=y==label
            ax.scatter(X_r[position,0],X_r[position,1],label="target= %d"%label,
            color=color)
        ax.set_xlabel("X[0]")
        ax.set_xticks([]) # 隐藏 x 轴刻度
        ax.set_yticks([]) # 隐藏 y 轴刻度
        ax.set_ylabel("X[1]")
        ax.legend(loc="best")
        ax.set_title(r"$ (%s (x \cdot z+1)+%s)^{%s}$"%(gamma,r,p))
    plt.suptitle("KPCA-Poly")
    plt.show()
def plot_KPCA_rbf(*data):
    '''
    绘制经过 使用 rbf 核的KernelPCA 降维到二维之后的样本点
    :param data: 可变参数。它是一个元组，这里要求其元素依次为：训练样本集、训练样本的标记
    :return: None
    '''
    X,y=data
    fig=plt.figure()
    colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),
        (0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)# 颜色集合，不同标记的样本染不同的颜色
    Gammas=[0.5,1,4,10]# rbf 核的参数组成的列表。每个参数就是 gamma值
    for i,gamma in enumerate(Gammas):
        kpca=decomposition.KernelPCA(n_components=2,kernel='rbf',gamma=gamma)
        kpca.fit(X)
        X_r=kpca.transform(X)# 原始数据集转换到二维
        ax=fig.add_subplot(2,2,i+1)## 两行两列，每个单元显示核函数为 rbf 的 KernelPCA 一组参数的效果图
        for label ,color in zip( np.unique(y),colors):
            position=y==label
            ax.scatter(X_r[position,0],X_r[position,1],label="target= %d"%label,
            color=color)
        ax.set_xlabel("X[0]")
        ax.set_xticks([]) # 隐藏 x 轴刻度
        ax.set_yticks([]) # 隐藏 y 轴刻度
        ax.set_ylabel("X[1]")
        ax.legend(loc="best")
        ax.set_title(r"$\exp(-%s||x-z||^2)$"%gamma)
    plt.suptitle("KPCA-rbf")
    plt.show()
def plot_KPCA_sigmoid(*data):
    '''
    绘制经过 使用 sigmoid 核的KernelPCA 降维到二维之后的样本点
    :param data: 可变参数。它是一个元组，这里要求其元素依次为：训练样本集、训练样本的标记
    :return: None
    '''
    X,y=data
    fig=plt.figure()
    colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),
        (0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)# 颜色集合，不同标记的样本染不同的颜色
    Params=[(0.01,0.1),(0.01,0.2),(0.1,0.1),(0.1,0.2),(0.2,0.1),(0.2,0.2)]# sigmoid 核的参数组成的列表。
        # 每个元素就是一种参数组合（依次为 gamma,coef0）
        # gamma 取值为： 0.01，0.1，0.2
        # coef0 取值为： 0.1,0.2
        # 排列组合一共有 6 种组合
    for i,(gamma,r) in enumerate(Params):
        kpca=decomposition.KernelPCA(n_components=2,kernel='sigmoid',gamma=gamma,coef0=r)
        kpca.fit(X)
        X_r=kpca.transform(X)# 原始数据集转换到二维
        ax=fig.add_subplot(3,2,i+1)## 三行两列，每个单元显示核函数为 sigmoid 的 KernelPCA 一组参数的效果图
        for label ,color in zip( np.unique(y),colors):
            position=y==label
            ax.scatter(X_r[position,0],X_r[position,1],label="target= %d"%label,
            color=color)
        ax.set_xlabel("X[0]")
        ax.set_xticks([]) # 隐藏 x 轴刻度
        ax.set_yticks([]) # 隐藏 y 轴刻度
        ax.set_ylabel("X[1]")
        ax.legend(loc="best")
        ax.set_title(r"$\tanh(%s(x\cdot z)+%s)$"%(gamma,r))
    plt.suptitle("KPCA-sigmoid")
    plt.show()
if __name__=='__main__':
    X,y=load_data() # 产生用于降维的数据集
    test_KPCA(X,y)   # 调用 test_KPCA
    #plot_KPCA(X,y)   # 调用 plot_KPCA
    #plot_KPCA_poly(X,y)   # 调用 plot_KPCA_poly
    #plot_KPCA_rbf(X,y)   # 调用 plot_KPCA_rbf
    #plot_KPCA_sigmoid(X,y)   # 调用 plot_KPCA_sigmoid

总结一下：实例就是把鸢尾花这个4维数据降维降到2维的。从plot_KPCA_poly函数可以看到，采用同样的多项式函数，如果参数不同，其降维后的数据分布是不同的。其他函数亦是如此。

将数据转换成前N个主成分的伪代码大致如下：

  • 去除平均值
  • 计算协方差矩阵
  • 计算协方差矩阵的特征值和特征向量
  • 将特征值从大到小排序
  • 保留最上面的N个特征向量

  • 将数据转换到上述N个特征向量构建的新空间中

    PCA可以从数据中识别其主要特征，它是通过沿着数据最大方差方向旋转坐标轴来实现的。选择方差最大的方向作为第一条坐标轴，后续坐标轴与前面的坐标轴正交。协方差矩阵上的特征值分析可以用一系列的正交坐标轴来获取。

Lanbocsdn
关注
  • 3
    点赞
  • 踩
  • 25
    收藏
    觉得还不错? 一键收藏
  • 2
    评论
专栏目录
降维算法之PCA及其实战
huahuaxiaoshao的博客
01-07 1382
      主成分分析（Principal components analysis，以下简称PCA）是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。为什么说PCA应用广泛呢？PCA是一种无监督算法，也就是我们不需要标签也能对数据做降维，这就使得其应用范围更加广泛了。一般我们提到降维最容易想到的算法就是PCA，...
一种新的降维算法PCA_LLE在图像识别中的应用.pdf
05-17
一种新的降维算法PCA_LLE在图像识别中的应用 降维算法是机器学习和数据挖掘中的一种重要技术，旨在将高维度的数据转换为低维度的数据，减少数据维度从而提高数据处理效率。常见的降维算法有Principal Component ...
PCA降维算法
qq_53086801的博客
09-18 2873
PCA降维算法
机器学习：升维（Polynomial Regression）
最新发布
ma_no_lo的博客
04-26 741
升维的概念，目的，以及多项式回归。附有可视化的拟合曲线以及他们之间的区别
秒懂数据降维——主成分分析PCA
gjinc的博客
06-20 4505
主成分分析（Principal Component Analysis，简称 PCA）是一种常用的数据降维方法，旨在通过将高维数据投影到低维空间中的主要方向来捕获数据的本质结构。主成分分析可用于降低数据的维度，压缩图像、音频和视频数据，去除冗余信息等。
通俗理解PCA降维作用
热门推荐
HLBoy_happy的博客
08-13 8万+
本文主要介绍一种降维方法，PCA（Principal Component Analysis，主成分分析）。降维致力于解决三类问题。 1. 降维可以缓解维度灾难问题； 2. 降维可以在压缩数据的同时让信息损失最小化； 3. 理解几百个维度的数据结构很困难，两三个维度的数据通过可视化更容易理解。。
机器学习降维算法一：PCA(主成分分析算法)
weixin_30577801的博客
09-22 431
引言： 机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。 y是数据点映射后的低维向量表达，通常y的维度小于x的维度（当然提高维度也是可以的）。f可能是显式的或隐式的、线性的或非线性的。 目前大部分降维算法处理向量表达的数据，也有一些降维算法处理高...
python-特征降维算法PCA的python实现.zip
02-18
python python_特征降维算法PCA的python实现
NM_PCA.zip_PCA数据降维_pca_pca降维_降维_降维算法PCA
07-14
PCA降维算法，本程序已经调好，可以直接跑数据
pca降维算法.rar_PCA 降维_pca_pca 降维_pca算法_pca降维
07-14
pca降维算法，试验已经成功，将39维数据降到12维
PCA主成分分析（PCA降维）
褪色的博客
05-25 3931
PCA（Principal Components Analysis，主成分分析），作为一种降维技术，使数据更易用于分析数据集建立数据模型。PCA是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k（k
降维算法实现原理
weixin_41857483的博客
11-10 2063
0. 前言 上篇博客对于维度以及降维相关概念进行了说明，下面将学习什么是PCA，什么是SVD？ 1. PCA & SVD 前面也提到了，降维就是要减少特征的数目，也就是说会删除一部分数据，而在训练模型的时候，数据减少可能会影响模型的最终表现。除此之外，高维数据中，有一些特征是无效的，还有些特征可能是线性相关的。如果能有一种算法可以衡量特征上的信息，使得在降维的过程中，在减少特征数量的同时又能保留更多的有效的信息(想兼得鱼和熊掌)。也就是说，将那些重复的信息（线性相关的）合并一下，把无效的特征删除掉，
知识：PCA降维
weixin_44340277的博客
02-18 2733
参考了两篇关于PCA的帖子： CodingLabs - PCA的数学原理 【机器学习】降维——PCA（非常详细） - 知乎 里面讲的比较详细，我只做个小简化 PCA（Principal Component Analysis）：用于高维数据的降维，可用于提取数据的主要特征分量 这里需要一些数学的基础知识： 1. 内积和投影 设 A=(x1,y1)，B=(x2,y2)，那么A·B = x1*x2 + y1*y2 =|A|*|B|*cos(α)（α...
PCA的数学原理
wxing2008666的专栏
06-28 6303
PCA（Principal Component Analysis）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。网上关于PCA的文章有很多，但是大多数只描述了PCA的分析过程，而没有讲述其中的原理。这篇文章的目的是介绍PCA的基本数学原理，帮助读者了解PCA的工作机制是什么。 当然我并不打算把文章写成纯数
PCA降维深入理解
u012033832的博客
07-31 4107
网上资料非常多，大部分都是讲先求协方差，协方差怎么求的，但是没有讲为什么要求协方差，为什么要选特征值最大的特征，特征值最大到底代表了什么含义。 简单回忆：         计算协方差到底是选行还是选列呢，记住协方差矩阵是计算不同维度间的协方差，不是两个样本间的，所以我们求协方差的目的就是计算不同纬度之间的相关性，并选出特征值最大的前多少个纬度，把特征值小的纬度去掉，起到一个降维的作用 PCA...
降维算法--PCA理论、公式推导
huobumingbai1234的博客
12-08 2048
一、降维算法的主要的目的 1、降维可以减少数据共线性，减少冗余特征，提高算法运行效率 2、可视化需要 二、主要的降维算法 三、降维算法的主要思想 在高维数据中，有一部分特征是不带有有效信息的，还有一部分特征之间存在共线性(特征间有线性关系)，我们需要过滤掉这一部分特征。 PCA算法中，我们用方差表示特征是不是包含更多的信息...
常见的降维算法
在服务器上挂载OSS_bucket
01-11 1248
常见的降维算法： 线性方法 主成分分析（Principal Component Analysis,PCA）、 对应分析（Correspondence Ahalysis,CA)、 多重对应分析（Multiple Corresspondence Analysis,MCA）、 经典多维尺度分析（classical multidimensional scaling,cMDS）、 主坐标分析（Principal Coordinate Analysis,PCoA）。
干货｜机器学习-稀疏矩阵的处理
喜欢打酱油的老鸟
01-20 1万+
https://www.toutiao.com/a6647043426384609805/   2019-01-16 18:43:19   什么是稀疏矩阵？ 我们知道矩阵是一个由m行和n列组成的二维数据对象，因此一共有m x n个数值。当这个矩阵的绝大部分数值为零，且非零元素呈不规律分布时，则称该矩阵为稀疏矩阵（Sparse Matrix）。下图所示的是一个8 x 8的稀疏矩阵。 ...
请提供一种原理区别于Sklearn - PCA数据降维算法的PCA降维算法
05-24
一种原理区别于Sklearn-PCA数据降维算法的PCA降维算法是Kernel PCA（Kernel Principal Component Analysis），它通过将原始数据映射到高维特征空间中，然后在特征空间中进行PCA降维。具体来说，Kernel PCA使用核函数来计算原始数据点之间的相似性，将其转换为高维空间中的点，然后在该空间中执行PCA，以提取最大方差的成分。因此，Kernel PCA可以处理非线性数据，并且可以捕捉到数据中的非线性结构。相比之下，Sklearn-PCA数据降维算法是一种线性方法，只能处理线性数据，并且无法处理非线性结构的数据。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值