数据结构与算法系列----Sparse Table算法（RMQ问题）

一：背景

Sparse Table算法（简称ST算法）是针对RMQ问题的，什么是RMQ？

RMQ（Range Minimum/Maximum Query），即区间最值查询，是指这样一个问题：对于长度为n的数组arry[]，回答若干询问RMQ（A , i , j ）( 0<=i , j<=n-1 )，返回数列arry中下标在i，j之间的最小/大值。

这两个问题是在实际应用中经常遇到的问题，下面介绍一下解决这两种问题的比较高效的算法。当然，该问题也可以用线段树（也叫区间树）解决，算法复杂度为O(N)~O(logN)，这里我们暂不介绍。

其实想想，找一个区间最值，最简单的直接比较，复杂度也是O(n)，所以如果查找次数很少，用ST没有意义。ST的应用场景就是要对一个数串查询多次的情况。基本思想是对串中所有可能的区间组合的最值用二维数组保存，也就是所谓的预处理，查询时直接数组下标获取，O(1)的时间。下面采用动态规划来对数串进行预处理，也就是填充二维数组。

二：算法分析

设arry[]是要求区间最值的数组，maxArry[i][j]是DP所需的二维数组。其中maxArry[i][j]表示从下标为i开始连续2^j个数中的最大值，也就是arry[i]到arry[i+2^j-1]里的最大值（DP的状态）。

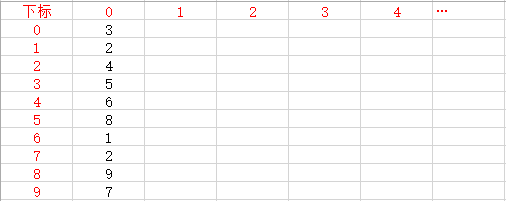
对于arry[ ] = { 3,2,4,5,6,8,1,2,9,7 }，

maxArry[ 0 ][ 0 ]=max( 3 )=3，

maxArry[ 0 ][ 1 ]=max( 3 , 2 )=3，

maxArry[ 1 ][ 2 ]=max( 2 , 4 , 5 , 6 )=6。

并且很容易发现maxArry[ i ][ 0 ]=arry[ i ]（DP的初值）。

也就是下图：

好，现在DP的状态和初值都有了。那状态转移方程呢？

我们把maxArry[ i ][ j ]分成两段,也就是arry[ i ]到arry[ i+2^j-1 ]这些个数(一定是偶数个）分为两段：

arry[ i ]......arry[ i+2^( j-1 )-1 ]和arry[ i+2^( j-1 ) ]......arry[ i+2^j-1 ]

于是得到状态转移方程：maxArry[ i ][ j ]=max( maxArry[ i ][ j-1 ],maxArry[ i+2^( j-1 ) ][ j-1 ] )

代码如下：

void RMQ(int arry[], int arryLen)
{
	for (int i = 0; i < arryLen; i++)
	{
		maxArry[i][0] = arry[i];
		minArry[i][0] = arry[i];
	}

	int k = log(arryLen) / log(2.0);

	for (int j = 1; j <= k; j++)
	{
		for (int i = 0; i < arryLen; i++)
		{
			if (i + (1 << j) - 1 < arryLen)
			{
				maxArry[i][j] = max(maxArry[i][j - 1], maxArry[i + (1 << (j - 1))][j - 1]);
				minArry[i][j] = min(minArry[i][j - 1], minArry[i + (1 << (j - 1))][j - 1]);
			}
		}
	}
}

这里我们需要注意的是循环的顺序，我们发现外层是j，内层是i，这是为什么呢？可以是i在外，j在内吗？
答案是不可以。因为我们需要理解这个状态转移方程的意义。
状态转移方程的含义是：先更新所有长度为maxArry[i,0]即1个元素，然后通过2个1个元素的最值，获得所有长度为maxArry[i,1]即2个元素的最值，然后再通过2个2个元素的最值，获得所有长度为maxArry[i,2]即4个元素的最值，以此类推更新所有长度的最值。
而如果是i在外，j在内的话，我们更新的顺序就是maxArry[1,0],maxArry[1,1],maxArry[1,2],maxArry[1,3],表示更新从0开始1个元素，2个元素，4个元素，8个元素的最值。

最后开始查询，假如我们需要查询的区间为(i,j)，那么我们需要找到覆盖这个闭区间(左边界取i，右边界取j)的最小幂（可以重复，比如查询5，6，7，8，9，我们可以查询5678和6789）。

因为这个区间的长度为j - i + 1,所以我们可以取k=log2( j - i + 1)，则有：RMQ(arry, i, j)=max{maxArry[i , k], maxArry[ j - 2 ^ k + 1, k]}。
举例说明，要求区间[2，8]的最大值，k = log2（8 - 2 + 1）= 2，即求max(maxArry[2, 2]，maxArry[8 - 2 ^ 2 + 1, 2]) = max(maxArry[2, 2]，maxArry[5, 2])；

三：完整代码

#include<iostream>
#include<algorithm>
#include<cmath>

using namespace std;

//假设数组元素不超过1000个，则DP所用的数组大小为：
const int ROW = 1000 + 10;
const int COLUMN = 10 + 5;//log(1000)/log(2.0)~9.96

int maxArry[ROW][COLUMN];
int minArry[ROW][COLUMN];

void RMQ(int arry[], int arryLen)
{
	for (int i = 0; i < arryLen; i++)
	{
		maxArry[i][0] = arry[i];
		minArry[i][0] = arry[i];
	}

	int k = log(arryLen) / log(2.0);

	for (int j = 1; j <= k; j++)
	{
		for (int i = 0; i < arryLen; i++)
		{
			if (i + (1 << j) - 1 < arryLen)
			{
				maxArry[i][j] = max(maxArry[i][j - 1], maxArry[i + (1 << (j - 1))][j - 1]);
				minArry[i][j] = min(minArry[i][j - 1], minArry[i + (1 << (j - 1))][j - 1]);
			}
		}
	}
}


int main()
{
	int arry[] = { 3,2,4,5,6,8,1,2,9,7 };
	int len = sizeof(arry) / sizeof(int);

	RMQ(arry, len);

	cout << "数组的下标范围为：0 -- " << len - 1 << endl;
	cout << "请输入需要查询的下标范围（0 <= src <= des <= 9）: \n";
	int src, des;
	while (cin >> src >> des)
	{
		int k = log(des - src + 1.0) / log(2.0);

		int maxAns = max(maxArry[src][k], maxArry[des - (1 << k) + 1][k]);
		int minAns = min(minArry[src][k], minArry[des - (1 << k) + 1][k]);

		cout << "最大值是： " << maxAns << ", 最小值是： " << minAns << endl;
	}

	return 0;
}

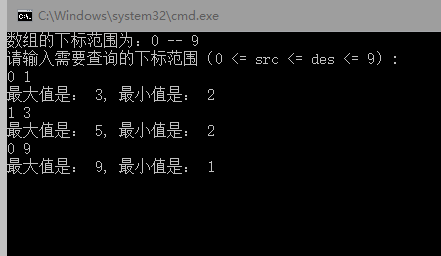
四：数据测试

返回目录---->数据结构与算法目录

参考： http://blog.csdn.net/liang5630/article/details/7917702   ，   http://blog.csdn.net/zhangjun03402/article/details/50440136