数据结构与算法系列----平衡二叉树（AVL树）

最新推荐文章于 2024-01-28 17:35:49 发布
最新推荐文章于 2024-01-28 17:35:49 发布
阅读量2.2k 收藏 3
点赞数 2
分类专栏： ACM 与数据结构 文章标签： 平衡二叉树 AVL 数据结构 C++ 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/LaoJiu_/article/details/51898992
版权 
一：背景

平衡二叉树（又称AVL树）是二叉查找树的一个进化体，由于二叉查找树不是严格的O(logN)，所以引入一个具有平衡概念的二叉树，它的查找速度是O(logN)。所以在学习平衡二叉树之前，读者必须需要了解下二叉查找树，具体链接：二叉查找树


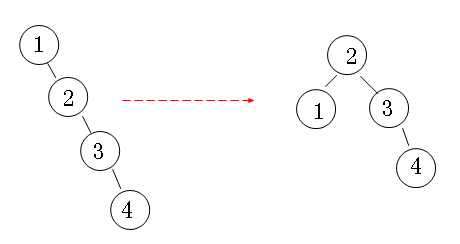
那么平衡是什么意思？我们要求对于一棵二叉查找树 ，它的每一个节点的左右子树高度之差不超过1。（对于树的高度的约定：空节点高度是0；叶子节点高度是1。）例如下图：


在进行下面的分析之前，我们先对AVL树作个概述，让读者先了解其运作机制，而后读者接下来的阅读才会容易许多。


我们为何说普通的二叉查找树不是严格的O(logN)复杂度呢？可以试想，如果我们插入的是一组有序上升或下降的数据，必然造成二叉查找树退化成一个单链表，其深度就是链表长度，查找效率为O（n），与我们想要的O(logN)比起相形见绌，因此我们想到“平衡”这个概念，继而引入二叉查找树，这就是我们接下来要讲的“平衡二叉树”，上图已经完美诠释了“平衡”的概念，读者可以再看一遍。


讲到平衡，那又如何去平衡呢？如何判断失衡呢？判断失衡很简单，我们只需在节点里加个变量，不妨设为m_height，其意义是该节点下的树的高度，在插入数据或者删除数据时我们要判断这个节点的左右儿子节点的高度之差是否大于1即可。


当我们发现该节点不平衡，我们自然需要对其做些处理，使其满足平衡。经过分析，在插入数据或者删除数据时只会有四种失衡的情况，所以我们需要对这四种情况分别写出应对的代码。这也就是我们第二部分即将要讲的四种应对之策----旋转。旋转学完，接下来的内容就不是很难了，无非就是插入，删除，查找，打印了，和二叉查找树差不多，唯一的区别就是判断失衡和失衡后的旋转，代码都有注释，一看就懂。


好，接下来先看下我们给AVL树定义的节点结构，代码如下：

typedef struct Node
{
	int m_key;
	int m_height;
	Node* m_lChild;
	Node* m_rChild;
	Node(int key)
	{
		m_key = key;
		m_height = 1;
		m_rChild = m_lChild = nullptr;
	}
}* PNode;


二：旋转算法

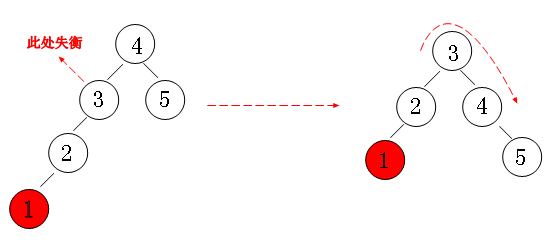
1.左左情况


节点3的左子树比右子树高2，左节点2的左子树比右子树高，这称为左左情况。

/* 左左情况，p指向失衡点，即图例中3 */
PNode LL_Rotate(PNode & p)
{
	cout << "LL\n";

	PNode top = p->m_lChild;
	p->m_lChild = top->m_rChild;
	top->m_rChild = p;

	p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;
	top->m_height = max(Height(top->m_lChild), Height(top->m_rChild)) + 1;

	return top;
}

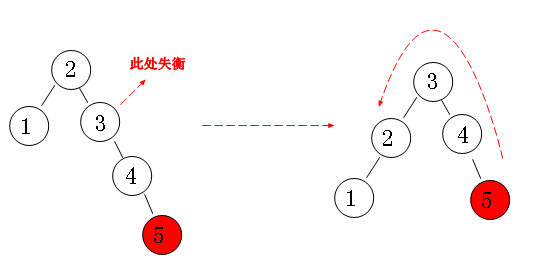
2.右右情况

节点3的右子树比左子树高2，右节点4的右子树比左子树高，这称为右右情况。

/* 右右情况，p指向失衡点，即图例中3 */
PNode RR_Rotate(PNode & p)
{
	cout << "RR\n";

	PNode top = p->m_rChild;
	p->m_rChild = top->m_lChild;
	top->m_lChild = p;

	p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;
	top->m_height = max(Height(top->m_lChild), Height(top->m_rChild)) + 1;

	return top;
}

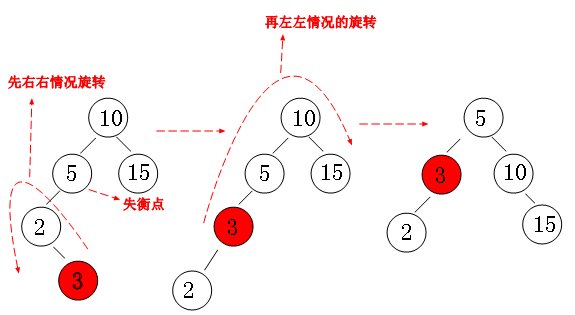
3.左右情况

节点5的左子树比右子树高2，左节点2的右子树比左子树高，这称为左右情况。

/* 左右情况，p指向失衡点，即图例中5 */
PNode LR_Rotate(PNode & p)
{
	cout << "LR\n";

	p->m_lChild = RR_Rotate(p->m_lChild);
	return LL_Rotate(p);
}

4.右左情况

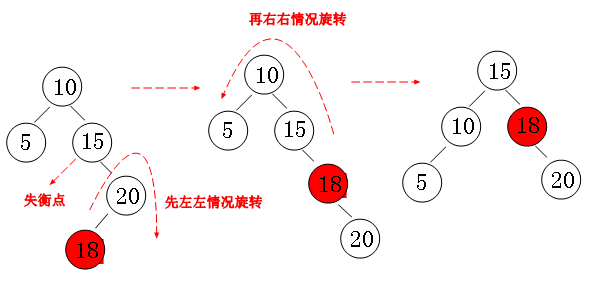
节点15的右子树比左子树高2，右节点20的左子树比右子树高，这称为右左情况。

/* 右左情况，p指向失衡点，即图例中15 */
PNode RL_Rotate(PNode & p)
{
	cout << "RL\n";

	p->m_rChild = LL_Rotate(p->m_rChild);
	return RR_Rotate(p);
}

三：其它算法实现

在写之前，先看两个辅助函数：

/* 计算当前节点的高度 */
int Height(PNode & p)
{
	return (p == nullptr) ? 0 : p->m_height;
}

/* 找到该节点下的最小值节点，返回该最小值，注意参数不是引用传递 */
int FindMin(PNode  p)
{
	while (p->m_lChild)
		p = p->m_lChild;
	return p->m_key;
}

1.插入

利用递归，我们先将节点插入，插入成功即递归结束，在一层一层的结束时，然后判断经过的每个节点的左右子树高度差，进行调整。

/* 添加操作 */
bool Add(int key, PNode & p)
{
	if (p == nullptr)
	{
		p = new Node(key);
		return true;
	}
	else
	{
		if (key == p->m_key)//已存在，直接退出
			return false;

		if (key < p->m_key)//左子树
		{
			if (Add(key, p->m_lChild))//是否成功插入
			{
				if (Height(p->m_lChild) - Height(p->m_rChild) == 2)//高度差等于2，得旋转调整
				{
					if (key < p->m_lChild->m_key)
						p = LL_Rotate(p);//左左情况
					else
						p = LR_Rotate(p);//左右情况
				}
				p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;//更新高度
				return true;
			}
			else
				return false;
		}

		else //右子树
		{
			if (Add(key, p->m_rChild))
			{
				if (Height(p->m_lChild) - Height(p->m_rChild) == -2)
				{
					if (key > p->m_rChild->m_key)
						p = RR_Rotate(p);
					else
						p = RL_Rotate(p);
				}
				p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;//更新高度
				return true;
			}
			else
				return false;
		}
	}
}

2.删除

删除的节点一共三种类型：有左右孩子；没有左右孩子；只有一个孩子（左或者右）。

其中对于第一种情况，也就是该节点是有左右孩子的，这里用了一个巧妙的方法，利用转化的思想，具体看代码，把这种情况转化为第二种或第三种。

/* 删除操作 */
bool Delete(int key, PNode & p)
{
	if (p == nullptr)
		return false;
	else
	{
		if (key == p->m_key)//找到该点
		{
			if (p->m_lChild && p->m_rChild)//左右孩子都存在
			{
				p->m_key = FindMin(p->m_rChild);//找到该节点下的最小节点
				Delete(p->m_key, p->m_rChild);//转化为: 删除找到的这个最小节点
			}
			else if (!p->m_lChild && !p->m_rChild)//左右孩子都不存在
			{
				PNode t = p;//注意p是引用类型
				p = nullptr;
				delete t;
				return true;
			}
			else//左右孩子只存在一个
			{
				PNode t = p;
				p = (p->m_lChild == nullptr) ? p->m_rChild : p->m_lChild;
				delete t;
				return true;
			}
		}

		else if (key < p->m_key)//在左子树删除
		{
			if (Delete(key, p->m_lChild))
			{
				if (Height(p->m_lChild) - Height(p->m_rChild) == 2)
				{
					if (key < p->m_lChild->m_key)
						p = LL_Rotate(p);
					else
						p = LR_Rotate(p);
				}

				p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;
				return true;
			}
			else
				return false;
		}
		else//在右子树删除
		{
			if (Delete(key, p->m_rChild))
			{
				if (Height(p->m_lChild) - Height(p->m_rChild) == -2)
				{
					if (key > p->m_rChild->m_key)
						p = RR_Rotate(p);
					else
						p = RL_Rotate(p);
				}
				p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;
				return true;
			}
			else
				return false;
		}
	}
}

3.查找 
/* 查找操作 */
bool Find(int key, PNode & p)
{
	if (p == nullptr)
		return false;
	else
	{
		if (key == p->m_key)
			return true;
		else if (key < p->m_key)
			return Find(key, p->m_lChild);
		else
			return Find(key, p->m_rChild);
	}
}

4.层次遍历 

/* 层次遍历，和普通的层次遍历不一样，打印的结果模拟了树的形状 */
void PrintTheLevel(PNode & p, int level)
{
	if (p == nullptr || level <= 0)
		return;
	if (level == 1)
	{
		cout << p->m_key << "," << p->m_height << "  ";//输出节点及对应的高度
		return;
	}

	PrintTheLevel(p->m_lChild, level - 1);
	PrintTheLevel(p->m_rChild, level - 1);
}

void LevelOrder(PNode & p)
{
	int depth = Height(p);
	for (int i = 1; i <= depth; i++)
	{
		PrintTheLevel(p, i);//打印树的第i行
		cout << endl;
	}
}


四：完整代码

#define _CRT_SECURE_NO_DEPRECATE 
#define _CRT_SECURE_CPP_OVERLOAD_STANDARD_NAMES 1 

#include<iostream>
#include<algorithm>
using namespace std;

typedef struct Node
{
    int m_key;
    int m_height;
    Node* m_lChild;
    Node* m_rChild;
    Node(int key)
    {
        m_key = key;
        m_height = 1;
        m_rChild = m_lChild = nullptr;
    }
}* PNode;

PNode pRoot = nullptr;//根节点


/* 计算当前节点的高度 */
int Height(PNode & p)
{
    return (p == nullptr) ? 0 : p->m_height;
}

/* 找到该节点下的最小值节点，返回该最小值，注意参数不是引用传递 */
int FindMin(PNode  p)
{
    while (p->m_lChild)
        p = p->m_lChild;
    return p->m_key;
}

/* 左左情况 */
PNode LL_Rotate(PNode & p)
{
    cout << "LL\n";

    PNode top = p->m_lChild;
    p->m_lChild = top->m_rChild;
    top->m_rChild = p;

    p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;
    top->m_height = max(Height(top->m_lChild), Height(top->m_rChild)) + 1;

    return top;
}

/* 右右情况 */
PNode RR_Rotate(PNode & p)
{
    cout << "RR\n";

    PNode top = p->m_rChild;
    p->m_rChild = top->m_lChild;
    top->m_lChild = p;

    p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;
    top->m_height = max(Height(top->m_lChild), Height(top->m_rChild)) + 1;

    return top;
}

/* 左右情况 */
PNode LR_Rotate(PNode & p)
{
    cout << "LR\n";

    p->m_lChild = RR_Rotate(p->m_lChild);
    return LL_Rotate(p);
}

/* 右左情况 */
PNode RL_Rotate(PNode & p)
{
    cout << "RL\n";

    p->m_rChild = LL_Rotate(p->m_rChild);
    return RR_Rotate(p);
}

/* 添加操作 */
bool Add(int key, PNode & p)
{
    if (p == nullptr)
    {
        p = new Node(key);
        return true;
    }
    else
    {
        if (key == p->m_key)//已存在，直接退出
            return false;

        if (key < p->m_key)//左子树
        {
            if (Add(key, p->m_lChild))//是否成功插入
            {
                if (Height(p->m_lChild) - Height(p->m_rChild) == 2)//高度差等于2，得旋转调整
                {
                    if (key < p->m_lChild->m_key)
                        p = LL_Rotate(p);//左左情况
                    else
                        p = LR_Rotate(p);//左右情况
                }
                p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;//更新高度
                return true;
            }
            else
                return false;
        }

        else //右子树
        {
            if (Add(key, p->m_rChild))
            {
                if (Height(p->m_lChild) - Height(p->m_rChild) == -2)
                {
                    if (key > p->m_rChild->m_key)
                        p = RR_Rotate(p);
                    else
                        p = RL_Rotate(p);
                }
                p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;//更新高度
                return true;
            }
            else
                return false;
        }
    }
}

/* 删除操作 */
bool Delete(int key, PNode & p)
{
    if (p == nullptr)
        return false;
    else
    {
        if (key == p->m_key)//找到该点
        {
            if (p->m_lChild && p->m_rChild)//左右孩子都存在
            {
                p->m_key = FindMin(p->m_rChild);//找到该节点下的最小节点
                Delete(p->m_key, p->m_rChild);//转化为: 删除找到的这个最小节点
            }
            else if (!p->m_lChild && !p->m_rChild)//左右孩子都不存在
            {
                PNode t = p;//注意p是引用类型
                p = nullptr;
                delete t;
                return true;
            }
            else//左右孩子只存在一个
            {
                PNode t = p;
                p = (p->m_lChild == nullptr) ? p->m_rChild : p->m_lChild;
                delete t;
                return true;
            }
        }

        else if (key < p->m_key)//在左子树删除
        {
            if (Delete(key, p->m_lChild))
            {
                if (Height(p->m_lChild) - Height(p->m_rChild) == 2)
                {
                    if (key < p->m_lChild->m_key)
                        p = LL_Rotate(p);
                    else
                        p = LR_Rotate(p);
                }

                p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;
                return true;
            }
            else
                return false;
        }
        else//在右子树删除
        {
            if (Delete(key, p->m_rChild))
            {
                if (Height(p->m_lChild) - Height(p->m_rChild) == -2)
                {
                    if (key > p->m_rChild->m_key)
                        p = RR_Rotate(p);
                    else
                        p = RL_Rotate(p);
                }
                p->m_height = max(Height(p->m_lChild), Height(p->m_rChild)) + 1;
                return true;
            }
            else
                return false;
        }
    }
}

/* 查找操作 */
bool Find(int key, PNode & p)
{
    if (p == nullptr)
        return false;
    else
    {
        if (key == p->m_key)
            return true;
        else if (key < p->m_key)
            return Find(key, p->m_lChild);
        else
            return Find(key, p->m_rChild);
    }
}

/* 层次遍历，和普通的层次遍历不一样，打印的结果模拟了树的形状 */
void PrintTheLevel(PNode & p, int level)
{
    if (p == nullptr || level <= 0)
        return;
    if (level == 1)
    {
        cout << p->m_key << "," << p->m_height << "  ";//输出节点及对应的高度
        return;
    }

    PrintTheLevel(p->m_lChild, level - 1);
    PrintTheLevel(p->m_rChild, level - 1);
}

void LevelOrder(PNode & p)
{
    int depth = Height(p);
    for (int i = 1; i <= depth; i++)
    {
        PrintTheLevel(p, i);
        cout << endl;
    }
}

int main()
{


    
    return 0;
}







数据测试方面，请读者自行设计数据，针对各算法进行测试，博主设计的多组数据运行均正确。

若程序有错，请一定底下留言，博主会及时回复，谢谢。




返回目录---->数据结构与算法目录







图片资源来自及参考自：

http://www.cppblog.com/cxiaojia/archive/2012/08/20/187776.html

http://www.cnblogs.com/huangxincheng/archive/2012/07/22/2603956.html




LaoJiu_
关注
专栏目录
平衡树——AVL算法
_int_me的博客
05-02 1172
有关AVL树的解析
数据结构与算法分析--C语言描述_数据结构与算法_
10-01
常见的数据结构包括数组、链表、栈、队列、树（如二叉树、AVL树、红黑树）、图等。数组是最基础的数据结构，提供随机访问但插入和删除操作相对较慢；链表则通过指针链接元素，便于动态调整但访问速度较慢；栈和队列...
数据结构与算法（十三）平衡二叉树之AVL树
Chiclaim
06-19 1678
本文主要包括以下内容： 平衡二叉树的概念 AVL树 插入操作保持AVL树的平衡 删除操作保持AVL树的平衡 平衡二叉树的概念 为什么需要平衡二叉树？ 通过前面的 二分搜索树(Binary Search Tree)和 BinarySearchTree的时间复杂度分析 的介绍我们知道，二分搜索树的性能跟树的高度(h)有关系 ： h 为二分搜索树的高度，那么高度 h 和二分搜索树节...
数据结构与算法分析之平衡二叉树的建立
CSDN_564174144的博客
07-18 905
平衡二叉树的概念： 平衡二叉树是二叉查找树的一个进化体，也是第一个引入平衡概念的二叉树。平衡二叉树又称AVL树。 平衡二叉树的性质： 对于每个结点来说，它的左右子树的高度之差不能超过1，如果插入或者删除一个结点是的高度之差大于1，就要进行结点之间的旋转，将二叉树重新维持在一个平衡状态。 下面会一步一步的讲解如何写平衡二叉树，重点是平衡二叉树的核心部分，也就是旋转算法。-第一步：创建节点信息 相
AVL树的平衡算法（JAVA实现）
weixin_30243533的博客
12-02 105
1、概念： 　　AVL树本质上还是一个二叉搜索树，不过比二叉搜索树多了一个平衡条件：每个节点的左右子树的高度差不大于1。 二叉树的应用是为了弥补链表的查询效率问题，但是极端情况下，二叉搜索树会无限接近于链表，这种时候就无法体现二叉搜索树在查询时的高效率，而最初出现的解决方式就是AVL树。如下图： 2、旋转 　　说到AVL树就不得不提到树的旋转，旋转是AVL维持平衡的方式，主要有以...
平衡二叉树详解 通俗易懂
热门推荐
半亩方糖
01-10 13万+
平衡二叉树（AVL） 阅读之前请先了解 二叉搜索树 平衡二叉树定义：任意节点的子树的高度差都小于等于 1 1. 为什么使用「平衡二叉树」 二叉树能提高查询的效率 O(logn)，但是当你插入 {1,2,3,4,5,6} 这种数据的时候，你的二叉树就像一个「链表」一样，搜索效率变为 O(n) 于是在 1962 年，一个姓 AV 的大佬（G. M. Adelson-Velsky） 和一个姓 L 的大佬（ Evgenii Landis）提出「平衡二叉树」（AVL） 。 于是插入 {1,2,3,4,5,6}
算法-树形结构- 树与二叉树- 树的数据生成器.rar
09-16
3. **树的类型**：包括但不限于二叉搜索树、完全二叉树、满二叉树、平衡二叉树（如AVL树和红黑树）、B树和B+树等，每种类型的树有其特定的性质和应用场景。 4. **树的数据生成**：生成树的数据通常涉及随机生成算法...
数据结构与算法设计课程设计-二叉排序树与平衡二叉树.docx
06-28
在计算机科学领域，数据结构与算法设计是至关重要的部分，它们直接影响到程序的效率和性能。本课程设计主要探讨了两种特殊类型的二叉树：二叉排序树和平衡二叉树，尤其是AVL树，这些都是在数据存储和检索中常用的...
数据结构与算法-二叉树的创建与操作
最新发布
04-21
在IT领域，数据结构与算法是编程基础的重要组成部分，尤其对于C++开发者来说更是如此。本主题聚焦于“二叉树的创建与操作”，这是一种特殊的数据结构，它以树的形式存储数据，每个节点最多有两个子节点，通常称为左...
数据结构和算法-思维导图.pdf
05-26
- 平衡二叉树、红黑树、AVL树、满二叉树、完全二叉树。 8. **图论基础**： - 图的遍历形态，如广度优先搜索、深度优先搜索、中序遍历、前序遍历、后序遍历。 - 图论中的拓扑排序、最短路径、关键路径、最小生成...
平衡二叉树的建立c语言实现
09-03
平衡二叉树的建立c语言实现。详细的实现了对平衡二叉树的创建。通过这个能很好的理解平衡二叉树及其数据结构
平衡树、AVL树
atu99602的博客
01-03 149
平衡树 平衡树有AVL树、红黑树、2-3树、2-3-4树 AVL树 AVL树是最早的一种平衡树，它以发明者的名字命名；AVL是一种特殊的二叉搜索树，平移保证二叉搜索树的正确。 特征 在AVL树中节点的左子树和右子树的高度差不会大于1 实现 在AVL树中每个节点都存储着一个额外的数据，它的左子树和右子树的高度差，这个差值不能大于1。插入一个元素后，检查该元素所在的最低子树的根...
java avl_AVL树的平衡算法（JAVA实现）
weixin_39627405的博客
02-16 179
2、旋转说到AVL树就不得不提到树的旋转，旋转是AVL维持平衡的方式，主要有以下四种类型。2.1、左左旋转如图2-1所示，此时A节点的左树与右树的高度差为2，不符合AVL的定义，此时以B节点为轴心，AB间连线为转轴，将A节点旋转至B节点下方，由B节点的父节点变成子节点。实现所有节点的左右子树高度差小于等于1。如图2-2。2.2、右右旋转右右旋转与左左旋转类似，但是动作相反，如图2-3，2-4所示，...
【数据结构与算法】AVL树（平衡二叉树）
ambitionxzz的博客
02-24 423
给定结点数为n的AVL树最大高度为O(log2n) 树的高度：根节点高度为0，向下每层加一 左单旋(LL)，即麻烦结点在发现者左边的左边，解决方案是顺时针转，详情见Mooc PPT 右单旋(RR) 右-左双旋(RL)，左-右双旋(LR) typedef AVLNode *Position; typedef Position AVLTree; /*AVL树类型*/ struct AVLNo...
平衡二叉树（AVL树）（算法笔记）
Arabot_的博客
04-12 317
在上一节中，我们认识到了如果已知序列是一个有序序列，那么生成的BST将是一条链，查找的复杂度会达到O（n），这样就无法实现BST对数据查询优化的目的。所以AVL树就诞生了，其目的是为了使BST的高度在每次插入元素后仍然能保持O（logn）的级别，在建立BST的过程中，通过增加平衡调整功能，使任意结点的左子树和右子树的高度之差的绝对值不超过1，其中左子树与右子树的高度之差称为该结点的平衡因子。
算法：二叉平衡树（AVL树）
OceanStar的博客
10-07 7392
平衡二叉树定义 平衡二叉树 全称叫做 平衡二叉搜索（排序）树，简称 AVL树。英文：Balanced Binary Tree （BBT），注：二叉查找树(BST) AVL 什么意思？AVL 是大学教授 G.M. Adelson-Velsky 和 E.M. Landis 名称的缩写，他们提出的平衡二叉树的概念，为了纪念他们，将 平衡二叉树 称为 AVL树。 AVL树本质上是一颗二叉查找树，但是它又具有以下特点： 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1， 左右两个子树 也都是一棵平衡二叉树。
平衡二叉树
清风
05-01 4万+
1.定义 平衡二叉树，又称AVL树，用于解决二叉排序树高度不确定的情况，如果二叉排序树的子树间的高度相差太大，就会让二叉排序树操作的时间复杂度升级为O(n)，为了避免这一情况，为最坏的情况做准备，就出现了平衡二叉树，使树的高度尽可能的小，其本质还是一棵二叉搜索树。 平衡二叉树的性质： 左子树和右子树的高度之差的绝对值小于等于1 左子树和右子树也是平衡二叉树 为了方便起见，给树上的每个结点附加一个数字，给出该结点左子树与右子树的高度差，这个数字称为结点的平衡因子（BF） 平衡因子=结点左子树的高度-
【二叉树】平衡二叉树
StudyWinter的博客
01-28 1014
AVL树是最早被发明的自平衡二叉查找树。在AVL树中，任一节点对应的两棵子树的最大高度差为1，因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是O(logn)。增加和删除元素的操作则可能需要借由一次或多次树旋转，以实现树的重新平衡。AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis，他们在1962年的论文An algorithm for the organization of information 中公开了这一数据结构。
二叉树——平衡二叉树
csdn18529124315的博客
04-15 1307
平衡二叉树是二叉树变异，规则更加苛刻 想要将二叉树变为平衡二叉树，主要通过左旋和右旋来处理， 平衡二叉树和二叉树的区别是： 一：平衡二叉树要求重最上层的跟节点到最下面的叶节点经过的路程或者数据个数到小于或者与绝对值1 （根节点到叶节点的路径长度的最大值和最小值分别为a和b，那么a-b的绝对值要大于或等于1 ，如有 |a-b| >=1） 二：平衡树的根节点的左侧数据必须小于根节点，右侧树的数据必须大于根节点 开始解释平衡二叉树和二叉树的区别第一个点 下面开始上图（这个图只是普通的二叉树）： 从90到6
探索搜索树：二叉、AVL、红黑与B-树的原理与应用
数据结构与算法中的搜索树是一类重要的数据组织方式，它们在计算机科学中扮演着核心角色。本章节将深入探讨四种常见的搜索树类型：二叉搜索树、AVL树、红黑树以及B-树。 1. **二叉搜索树** (Binary Search Tree, ...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值