你需要掌握的算法：快慢指针

前言

在处理链表数据结构时，快慢指针是一种非常高效的算法技巧。它通过使用两个指针以不同的速度移动来解决链表中的各种问题，如检测链表是否有环、找到链表的中间节点、计算环的长度等。本文将详细介绍快慢指针的基本概念、主要应用及示例代码，帮助大家在实际开发中更好地理解和应用快慢指针。

龟兔赛跑

“龟兔赛跑” 的故事相信大家都不陌生，今天我们研究一个另类的龟兔赛跑。

乌龟和兔子同时从直线跑道的起点出发，乌龟的速度是 $v$，兔子的速度是 $2v$，现兔子已经进入环形跑道（进入环形跑道之后，只能沿着环形跑道运动）。

请问乌龟是否能追上兔子？乌龟若能追上兔子，那么乌龟和兔子将在何处相遇？

乌龟能否追上兔子

乌龟一定能追上兔子。因为兔子一直在环形跑道中，当乌龟进入环形跑道之后也将沿环形跑道不断运动。由于乌龟与兔子的速度不相等，两者不能保持相对静止，所以二者总会在某一位置相遇。

乌龟与兔子在何处相遇

乌龟与兔子在何处相遇，我们需要进行数学推导。

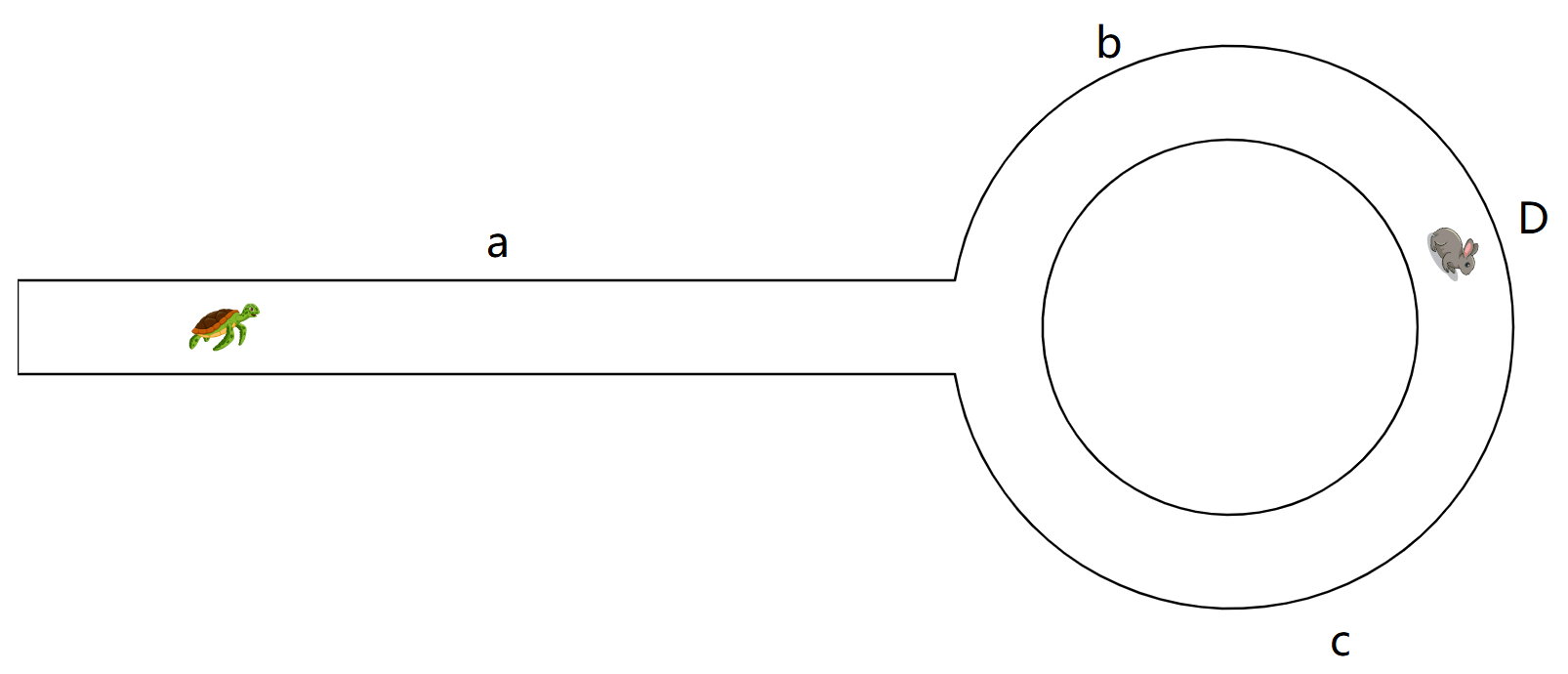
倘若直行跑道的总长度是 $a$，环形跑道的总长度是 $h$。

假设乌龟与兔子未来在 $D$ 点相遇，环形跑道起点到 $D$ 点的距离为 $b$，$D$ 点回到起点的距离为 $c$

则有：$h=b+c$

当乌龟与兔子相遇时，有：

乌龟的运动距离是：$a+b$

兔子的运动距离是：$a+nh+b=a+n(b+c)+b$，$n$ 表示环形跑道的圈数

因为乌龟的速度是 $v$，兔子的速度是 $2v$，则有：兔子的运动距离恒为乌龟运动距离的两倍

$2(a+b)=a+n(b+c)+b$

推导出：

$a=c+(n-1)(b+c)$，即：直行跑道的长度等于从相遇点 $D$ 到入环点的距离加上 $n-1$ 圈环长。

这个结果直观上并没有太大的意义。我们现做两个假设：

假设一：此时乌龟回到直线跑道的起点，兔子依旧在相遇点 $D$，现在它们重新都以速度 $v$ 运动。

此时会出现：当乌龟再次运动到入环点时，兔子也刚好重新运动到入环点。

假设二：兔子静止在相遇点 $D$，乌龟继续以速度 $v$ 运动

此时会出现：当乌龟再次和兔子相遇时，刚好是环的长度

龟兔问题的推论

通过研究龟兔问题我们可以有以下几个推论：

1. 龟兔问题可以用于检测环形（乌龟和兔子如果能够相遇一定存在环）
2. 若有环，可以找出环的入口点
3. 若有环，可以计算出环的长度

快慢指针

基础概念

快慢指针（Two Pointers/Floyd’s Tortoise and Hare Algorithm）是一种经典的算法技巧，用于解决链表、数组等数据结构中的问题。该方法最著名的应用是检测链表中的环，通常称为弗洛伊德循环检测算法（Floyd’s Cycle Detection Algorithm），或龟兔赛跑算法。它使用两个指针：慢指针和快指针。

• 慢指针：每次移动一步。
• 快指针：每次移动两步。

即，快指针是慢指针速度的 $2$ 倍（$v_{\text{fast}}=2v_{\text{slow}}$）

发展历史

• 快慢指针算法最早由罗伯特·弗洛伊德（Robert W. Floyd）在 1967 年提出。他在论文中描述了如何使用快慢指针解决循环检测问题。
• 在快慢指针方法被广泛应用后，许多编程教材和算法书籍将该算法称为龟兔赛跑算法（Tortoise and Hare Algorithm），灵感来源于古希腊伊索寓言中的“龟兔赛跑”故事。在这算法中，慢指针代表 “乌龟”，快指针代表 “兔子”，虽然兔子（快指针）比乌龟（慢指针）快，但它绕圈时最终会被乌龟追上。

快慢指针的应用

检测链表是否有环

使用快慢指针可以有效地检测链表中是否存在环。快指针每次移动两步，慢指针每次移动一步。如果链表中存在环，则快指针和慢指针最终会在环内相遇。如果链表没有环，则快指针会到达链表末尾。

public boolean detectCycle(ListNode head) {
    // 初始化两个指针：slow 和 fast，都指向链表的头节点
    ListNode slow = head, fast = head;

    // 使用 while 循环遍历链表，条件是 fast 不能为 null 且 fast.next 不能为 null
    while (fast != null && fast.next != null) {
        slow = slow.next;           // slow 指针每次走一步
        fast = fast.next.next;      // fast 指针每次走两步

        // 检查快指针和慢指针是否相遇（即 slow == fast）
        if (slow == fast) {
            // 如果相遇，说明链表中存在环
            return true;
        }
    }

    return false;
}

找到链表的中间节点

使用快慢指针可以高效地找到链表的中间节点。慢指针每次移动一步，快指针每次移动两步。当快指针到达链表末尾时，慢指针正好到达中间节点。

public ListNode findMiddle(ListNode head) {
    // 初始化两个指针：slow 和 fast，都指向链表的头节点
    ListNode slow = head, fast = head;

    // 使用 while 循环遍历链表，条件是 fast 不能为 null 且 fast.next 不能为 null
    while (fast != null && fast.next != null) {
        slow = slow.next;           // slow 指针每次走一步
        fast = fast.next.next;      // fast 指针每次走两步
    }

    // 当 fast 走到链表的末尾时，slow 指针正好位于链表的中间节点
    return slow; // 返回中间节点
}

计算链表的环长度

在检测到链表中存在环后，可以使用快慢指针计算环的长度。首先，快慢指针相遇时，计算环中节点的数量，直到再次遇到快指针。

public int calculateCycleLength(ListNode head) {
    // 初始化快慢指针，slow 和 fast 都指向链表的头节点
    ListNode slow = head, fast = head;

    // 变量 hasCycle 用来标记是否检测到环
    boolean hasCycle = false;

    // 检测环的存在
    // 使用 while 循环遍历链表，条件是 fast 和 fast.next 不能为 null
    while (fast != null && fast.next != null) {
        slow = slow.next;           // slow 每次走一步
        fast = fast.next.next;      // fast 每次走两步

        // 如果 slow 和 fast 相遇，说明存在环
        if (slow == fast) {
            hasCycle = true;        // 标记检测到环
            break;                  // 退出循环，开始计算环的长度
        }
    }

    // 如果没有检测到环，直接返回 0，表示没有环
    if (!hasCycle) return 0;

    // 计算环的长度
    int length = 0;                // 初始化长度变量为 0

    // 使用 do-while 循环遍历环，直到 slow 再次和 fast 相遇
    do {
        slow = slow.next;          // slow 每次走一步
        length++;                  // 每走一步，环的长度加 1
    } while (slow != fast);        // 当 slow 再次与 fast 相遇时，说明遍历了一圈

    // 返回环的长度
    return length;
}

找到链表环的入口节点

在检测到链表中有环之后，可以通过快慢指针找到环的入口节点。将一个指针从链表头部开始移动，另一个指针从环内相遇点开始移动，两者相遇的节点即为环的入口。

public ListNode findCycleStart(ListNode head) {
    // 初始化两个指针 slow 和 fast，都指向链表的头节点
    ListNode slow = head, fast = head;

    // 开始遍历链表，使用快慢指针法来检测环的存在
    while (fast != null && fast.next != null) {
        slow = slow.next;           // slow 每次走一步
        fast = fast.next.next;      // fast 每次走两步

        // 当 slow 和 fast 相遇时，说明链表中存在环
        if (slow == fast) {

            // 找到环之后，初始化一个新的指针 entry，指向链表的头节点
            ListNode entry = head;

            // 现在我们有两个指针：一个从头开始（entry），一个从相遇点开始（slow）
            // 两个指针每次都向前走一步，直到它们相遇，那个相遇点就是环的入口
            while (entry != slow) {
                entry = entry.next; // entry 每次向前走一步
                slow = slow.next;   // slow 也每次向前走一步
            }

            // 两个指针在环的入口相遇，返回该入口节点
            return entry;
        }
    }

    // 如果没有检测到环，返回 null，说明链表中没有环
    return null;
}

小结

快慢指针是一种高效的算法技巧，特别适用于链表问题。它通过两个指针以不同速度移动来解决问题，可以有效地检测链表中的环、找到中间节点、计算环的长度以及找到环的入口节点。