树链剖分 简单讲解

如果我们想对一棵树上一个节点到另一个节点的路径进行求和，求极值，修改等操作，单单借助线段树是远远不够的，这个时候我们就需要借用树链剖分的帮助。

树链剖分，顾名思义，树链，指的是树上的路径，剖分就是把树上的各条路径分为重链，轻链。

套用卿学姐的话，树链剖分其实就是一个对树上属性进行hash的一个过程，将树型结构hash成链式结构，再将这些链放至线段树，树状数组等数据结构来解决问题。

学习树链剖分首先要先知道以下几个概念：

1、重儿子：如果v是节点u的儿子节点中子树节点数最大的节点，那么v就是u的重儿子；

2、轻儿子：节点u除了v以外其他的儿子节点；

3、重边：节点u与其重儿子之间的连边；

4、轻边：节点u与其轻儿子之间的连边；

5、重链：由重边所连成的链；

6、轻链：由轻边所连成的链。

在树链剖分的过程中，我们需要调用一些数组来存储这棵树的一些信息：

1、sz[x] : 以x为根节点的子树的节点数；2、son[x] ：节点x的重儿子；3、fa[x] ：节点x的父亲节点；

4、dep[x]：节点x在这棵树种的深度；5、top[x]：节点x所在的链的端点；

6、id[x]：节点x与其父亲节点的连边在树链剖分之后的编号（也就是用来记录这条边或者点在线段树中的位置，注意在一条链上的所有编号必然是连续的）。

算法实现过程：

1、第一遍dfs遍历一遍整棵树，将sz，son，fa，dep这些信息处理出来；（这个过程较简单就不详细讲了，看看代码就行了）

void dfs1(int u){
    sz[u] = 1;son[u] = 0;
    for(int i = 0;i < E[u].size();i++){
        int v = E[u][i];
        if(v == fa[u]) continue;
        fa[v] = u;dep[v] = dep[u] + 1;
        dfs1(v);
        sz[u] += sz[v];
        if(sz[v] > sz[son[u]]) son[u] = v;
    }
}

2、第二遍dfs我们就可以借助第一遍dfs得到的信息将每条链的端点信息top以及每个点的编号id处理出来；根据定义，我们知道，如果一个节点v是其父亲节点的重儿子，那么这个节点肯定是跟父亲节点在一条链上的，那么这个节点所在链的端点必然和父亲节点相同，也就是top[u] = top[fa[u]]；如果一个节点v不是父亲节点的重儿子，那么它就会生成一条新的以自己为端点的链，也就是top[v] = v。那么从根节点往下不断的重复上面两个过程，就可以把top处理出来了，id在这个过程中也能一并处理出来。

void dfs2(int u,int tp){
    id[u] = ++tot;top[u] = tp;
    if(son[u]) dfs2(son[u],tp);//重儿子的top是等于父亲节点的；
    for(int i = 0;i < E[u].size();i++){
        int v = E[u][i];
        if(v == fa[u] || v == son[u]) continue;
        dfs2(v,v);//轻儿子的top就是它本身；
    }
}

举一个简单的例子讲一下这个过程

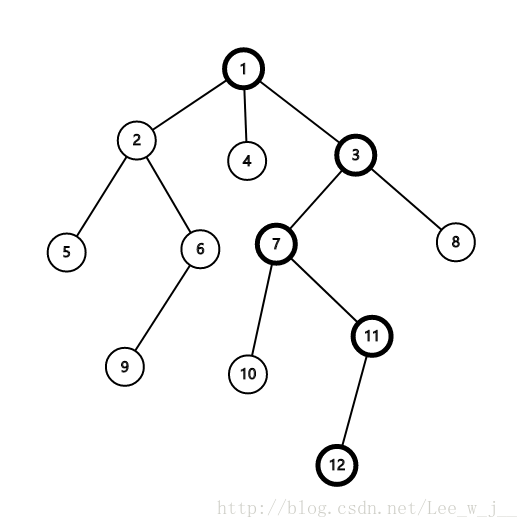
第一次dfs之后，我们知道节点1的重儿子为3，3的重儿子为7，7的重儿子为11，11的重儿子为12，那么这些节点的top值就全都等于1，根据dfs的性质，他们的id编号必然是连续的，也就是在一条链上；同理在处理出重链之后，以节点2为top也就可以处理出第二条链2 - 6 - 9，重复这个过程就能将所有链处理出来了。

经过树剖之后剖出来的几条链分别为1-3-7-11-12（重链），2-6-9，4，5，8；

那么我们要怎么利用这些链来进行对树上路径的修改，查询呢？

假设我们要修改u到v之间路径的值，在学树链剖分之前，我们可能是去求u和v的LCA，再慢慢往上更新，而有了树链剖分之后，我们可以对路径进行成段更新，因为前面说了，在一条链上的的节点的id值是连续的，那么我们就可以一条链一条链的进行更新。

假设f1 = top[u]，f2 = top[v]，dep[f1] > dep[f2]，那么我们就可以利用线段树更新从u到f1这条路径上的值，再令u = fa[f1]，f1 = top[u]；重复上面的过程，直到u和v在同一条链上，再将u到v这条链更新就行了。

再根据上面的图说明下

假设我们要修改节点6到节点10这条路径上的值

假设u = 6，v = 10，那么f1 = 2，f2 = 10，一开始dep[f1] < dep[f2]的，那么就先修改（v，f2）这条路径上的值；

接下来v = fa[10] = 7，f2 = 1，此时dep[f1] > dep[f2]，接着修改（u，f1）这条路径上的值；

接下来u = fa[2] = 1，此时u和v就在一条链上了，我们就可以直接修改（u，v）这条路径上的值了。

下面给上代码，结合代码再理解理解这个过程即可。

void Update(int u,int v){//修改
    while(top[u] != top[v]){
        if(dep[top[u]] < dep[top[v]]) swap(u,v);
        update(id[top[u]],id[u],1,n,1);
        u = fa[top[u]];
    }
    if(dep[u] > dep[v]) swap(u,v);
    update(id[u]],id[v],1,n,1);
}

int solve(int op,int u,int v){
    //查询u到v的最大值和权值和
    int ans = 0;
    if(!op){
        while(top[u] != top[v]){
            if(dep[top[u]] < dep[top[v]]) swap(u,v);
            ans = max(ans,query_max(id[top[u]],id[u],1,n,1));
            u = fa[top[u]];
        }
        if(dep[u] > dep[v]) swap(u,v);
        ans = max(ans,query_max(id[u],id[v],1,n,1));
    } else{
        while(top[u] != top[v]){
            if(dep[top[u]] < dep[top[v]]) swap(u,v);
            ans += query_sum(id[top[u]],id[u],1,n,1);
            u = fa[top[u]];
        }
        if(dep[u] > dep[v]) swap(u,v);
        ans += query_sum(id[u],id[v],1,n,1);
    }
    return ans;
}