PRML读书笔记(二)

二值变量

伯努利分布

对于 $x\in\{0,1\},p(x=1|\mu)=\mu$，$x$ 的概率分布有

$$\begin{equation} \begin{array}{rcl} Bern(x|\mu) &=& \mu^x(1-\mu)^{1-x} \\ E[x] &=& \mu \\ var[x] &=& \mu(1-\mu) \end{array} \end{equation}$$

假设一个数据集 $\mathcal{D}=\{x_1,x_2,\dots,x_N\}$，$x_i$ 服从伯努利分布，并且独立同分布，那么

$$\begin{equation} \begin{array}{rcl} p(\mathcal{D}|\mu) &=& \prod_{n=1}^N{\mu^{x_n}(1-\mu)^{1-x_n} } \end{array} \end{equation} \tag{1}$$

我们能够通过最大化似然函数来求解 $\mu$，

$$\begin{equation} \begin{array}{rcl} \ln{p(\mathcal{D}|\mu)} &=& \sum_{n=1}^N{x_n\ln\mu+(1-x_n)\ln(1-\mu) } \\ \frac{\partial\ln{p}}{\partial\mu} &=& 0 \\ \Rightarrow \mu_{ML} &=& \frac{1}{N}\sum_{n=1}^Nx_n \\ \Rightarrow \mu_{ML} &=& \frac{m}{N} \\ \end{array} \end{equation}$$

由于 $x_i\in\{0,1\}$，如果设 $D$ 中 $m$ 个值为1的观测值，那么上式可以写成

$$\Rightarrow \mu_{ML} = \frac{m}{N}$$

假设我们抛一枚有损的硬币 $p(x=1|\mu)=\mu$ 可以不为0.5，如果 $\mathcal{D}$ 有3个观测值，而且全部为1，即头部向上，那么我们由最大似然函数得到的结果就是 $\mu_{ML}=1$，如果我们用这个值去预测以后的结果，明显准确率会十分差，这就是所谓的过拟合。

二项分布

假设我们已经知道观测值中总共有 $m$ 个值为1的观测值，那么对 $m$ 的概率分布有

$$\begin{equation} \begin{array}{rcl} Bin(x|N,\mu) &=& \binom{N}{m}\mu^m(1-\mu)^{N-m} \\ \end{array} \end{equation} \tag{2}$$

$$\begin{equation} \begin{array}{rcl} \binom{N}{m} &=& \frac{N!}{(N-m)!m!} \\ E[m] &=& N\mu \\ var[m] &=& N\mu(1-\mu) \end{array} \end{equation}$$
以上关于期望与方差的计算可以重新计算，或者用第一章习题1.10的结论直接得出。

贝塔分布

前面我们知道最大似然函数会容易过拟合，那么可以用贝叶斯分析来减小这个问题，但是之前我们先介绍一下贝塔分布

$$\begin{equation} \begin{array}{rcl} Beta(\mu|a,b) &=& \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\mu^{a-1}(1-\mu)^{b-1} \\ \end{array} \end{equation} \tag{3}$$

$$\begin{equation} \begin{array}{rcl} \Gamma(x) &=& \int_0^{\infty}{\mu^{x-1}\exp^{-\mu} }d\mu \\ E[\mu] &=& \frac{a}{a+b} \\ var[\mu] &=& \frac{ab}{(a+b)^2(a+b+1)} \end{array} \end{equation}$$

其中 $a,b$ 是超参数，当 $a,b$ 取不同值时，分布图如下所示：

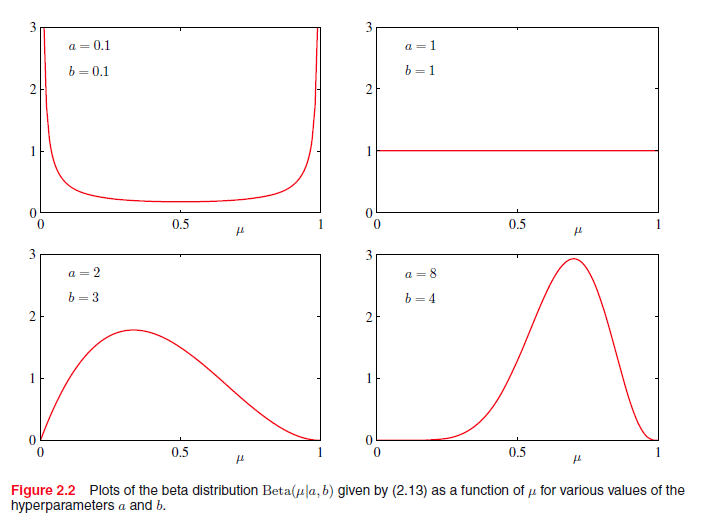
贝叶斯分析

贝叶斯公式：$p(y|x)\propto p(x|y)p(y)$

为了使过程简化，我们希望后验概率 $p(y|x)$ 与先验概率 $p(y)$ 有同样的形式，这个先验被称为共轭先验(conjugate prior)。对于抛硬币问题(服从伯努利分布)，由式(2)我们知道似然函数 $p(m|N,\mu) \propto \mu^m(1-\mu)^{N-m}$，那么我们可以取贝塔分布作为共轭先验，那么

$$\begin{equation} \begin{array}{rcl} p(\mu|m,l,a,b) &\propto& \mu^{m+a-1}(1-\mu)^{l+b-1} \\ m+l &=& N \\ \Rightarrow p(\mu|m,l,a,b) &=& \frac{\Gamma(a+b+l+m)}{\Gamma(a+m)\Gamma(b+l)}\mu^{a+m-1}(1-\mu)^{b+l-1} \\ \Rightarrow p(x=1|\mathcal{D}) &=& \int_0^1{p(x=1|\mu)p(\mu|D) }d\mu \\ &=& \int_0^1{\mu p(\mu|D) }d\mu \\ &=& E[\mu|D] \\ &=& \frac{a+m}{a+m+b+l} \end{array} \end{equation}$$

假设我们设 $a=1,b=1$，$\mathcal{D}$ 有三个观测值，并且都为1，那么在贝叶斯分析中去预测为 $\frac{4}{5}$，直觉上至少要比最大似然函数的预测 $1$ 要靠谱。

当 $N$ 越来越大时，先验知识就会被逐渐弱化，$\lim_{N\to\infty}\frac{a+m}{a+m+b+l} \simeq \frac{m}{N}$，最大后验与最大似然具有相同的预测值。但是对于数据量较少的应用，使用最大后验往往会比最大似然要好。

而且最大后验能够充当下一次观测数据的先验知识，从而达到顺序学习(sequential learning)，能够更好的应用于大规模数据。比如我们将 $\mathcal{D}$ 划分数据集大小为 $N_0,N_1$ 的两个子数据集 $\mathcal{D_0},\mathcal{D_1}$，刚开始我们观测到数据集 $\mathcal{D_1}$，先验知识为 $p(\mu|a_0,b_0)$，那么对于数据集 $\mathcal{D_0}$ 的后验为

$$\begin{equation} \begin{array}{rcl} p(\mu|m_0,l_0,a_0,b_0) &=& \frac{\Gamma(a_0+b_0+l_0+m_0)}{\Gamma(a_0+m_0)\Gamma(b_0+l_0)}\mu^{a_0+m_0-1}(1-\mu)^{b_0+l_0-1} \\ &=& Beta(\mu|a_0+m_0,b_0+l_0) \end{array} \end{equation}$$
然后我们观测到数据集 $\mathcal{D_1}$，此时以 $\mathcal{D_0}$ 的后验作为其先验，那么同理我们有
$$\begin{equation} \begin{array}{rcl} p(\mu|m_1,l_1,m_0,l_0,a_0,b_0) &=& \frac{\Gamma(a_0+b_0+l_0+m_0+l_1+m_1)}{\Gamma(a_0+m_0+m_1)\Gamma(b_0+l_0+l_1)}\mu^{a_0+m_0+m_1-1}(1-\mu)^{b_0+l_0+l_1-1} \\ &=& Beta(\mu|a_0+m_0+m_1,b_0+l_0+l_1) \\ &=& Beta(\mu|a_0+m,b_0+l) \\ \end{array} \end{equation}$$
这个优点能够使我们更容易的训练大规模数据。

在贝叶斯学习中，当我们观测的数据越来越多的时候，后验分布的不确定性就会越来越小。
todo

多元变量

前面一节我们介绍的是变量只有两个状态(要么是1，要么是0)，当变量有多个状态的时候，我们可以扩展成 $\mathbb{x} = (0,\dots,1,\dots,0)^T,\sum_{k=1}^Kx_k=1,p(x_k)=\mu_k$，那么

$$\begin{equation} \begin{array}{rcl} p(\mathbb{x}|\mathbb{\mu})=\prod_{k=1}^K\mu_k^{x_k} \end{array} \end{equation}$$
其中 $\mathbb{\mu}=(\mu_1,\dots,\mu_K)^T,\sum_{k=1}^K\mu_k=1$，同之前的伯努利分布一样，对于 $\mathcal{D}=\{\mathbb{x}_1,\dots,\mathbb{x}_N\}$ 的似然函数有
$$\begin{equation} \begin{array}{rcl} p(\mathcal{D}|\mathbb{\mu}) &=& \prod_{n=1}^{N}\prod_{k=1}^K\mu_k^{x_{nk}} \\ &=& \prod_{k=1}^K\mu_k^{\sum_{n=1}^{N}(x_{nk})} \\ &=& \prod_{k=1}^K\mu_k^{m_k} \\ \end{array} \end{equation}$$

求其最大值与二值变量是基本类似的，只是多了一个约束条件 $\sum_{k=1}^K\mu_k=1$，我们可以用拉格朗日乘子法来进行求解

$$\begin{equation} \begin{array}{rcl} L(\mathbb{\mu},\lambda) &=& \sum_{k=1}^K m_k\ln\mu_k+\lambda(\sum_{k=1}^K\mu_k-1) \\ \frac{\partial{L}}{\partial{\mu_k}} &=& 0 \\ \Rightarrow \frac{m_k}{\mu_k}+\lambda &=& 0 \\ \Rightarrow \mu_k &=& -m_k/\lambda \\ \frac{\partial{L}}{\partial{\lambda}} &=& 0 \\ \Rightarrow \lambda &=& -N \\ \Rightarrow \mu_k &=& -\frac{m_k}{N} \\ \end{array} \end{equation}$$

多项式分布

$$\begin{equation} \begin{array}{rcl} Mult(m_1,m_2,\dots,m_K|\mathbb{\mu},N) &=& \binom{N}{m_1m_2\dotsm_K}\prod_{k=1}^K\mu_k^{m_k} \\ \binom{N}{m_1m_2\dotsm_K} &=& \frac{N!}{m_1!m_2!\dots m_K!} \\ \sum_{k=1}^Km_k=N \end{array} \end{equation}$$

　狄利克雷(Dirichlet)分布

多项分布的共轭先验是狄利克雷分布，如下

$$\begin{equation} \begin{array}{rcl} p(\mathbb{\mu}|\mathbb{\alpha}) &\propto& \prod_{k=1}^K\mu_k^{\alpha_k-1} \\ Dir(\mathbb{\mu}|\mathbb{\alpha}) &=& \frac{\Gamma(\alpha_0)}{\Gamma(\alpha_1)\dotsm\Gamma(\alpha_K)}\prod_{k=1}^K\mu_k^{\alpha_k-1} \\ \alpha_0 &=& \sum_{k=1}^K\alpha_k \\ \end{array} \end{equation}$$

那么多项分布的后验

$$\begin{equation} \begin{array}{rcl} p(\mathbb{\mu}|\mathcal{D},\mathbb{\alpha}) &\propto& p(\mathcal{D}|\mathbb{\mu})p(\mathbb{\mu}|\mathbb{\alpha}) \propto \prod_{k=1}^K\mu_k^{\alpha_k+m_k-1} \\ p(\mathbb{\mu}|\mathcal{D},\mathbb{\alpha}) &=& \frac{\Gamma(\alpha_0+N)}{\Gamma(\alpha_1+m_1)\dotsm\Gamma(\alpha_K+m_K)}\prod_{k=1}^K\mu_k^{\alpha_k+m_k-1} \\ \end{array} \end{equation}$$

以上都是离散变量的分布，下面介绍连续型变量中最常用的分布，高斯(Gaussian)分布

高斯分布

对于单一变量：$\mathcal{N}(x|\mu,\sigma^2) =\frac{1}{\sqrt{2\pi \sigma^2}}\exp\{-\frac{(x-\mu)^2}{2\sigma^2}\}$

对于D维向量 $\mathbb{x}$：$\mathcal{N}(\mathbb{x}|\mathbb{\mu},\mathbb{\Sigma}) =\frac{1}{(2\pi)^{D/2 }|\mathbb{\Sigma}|^{1/2} }\exp\{-\frac{1}{2}(\mathbb{x}-\mathbb{\mu})^T\Sigma^{-1}(\mathbb{x}-\mathbb{\mu})\}$，其中 $\mathbb{\mu},\mathbb{\Sigma}$ 分别是D维均值向量和 $D\times D$ 协方差矩阵，$|\mathbb{\Sigma}|$ 是协方差矩阵的行列式。

对于单一变量，使其熵最大化的分布是高斯分布(PRML p54)，这个性质同样适用于多元(multivariate)高斯分布。中心极限定理告诉我们独立同分布的随机变量序列的和近似高斯分布。

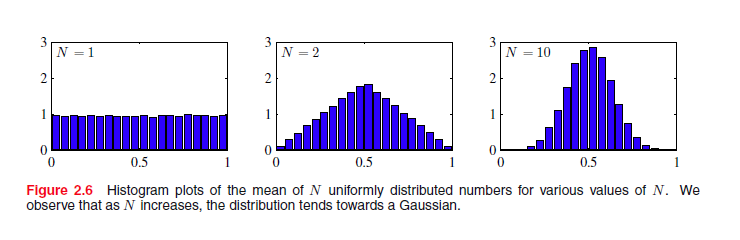
下面考虑一下高斯分布的几何形态

$$\begin{equation} \begin{array}{rcl} \Delta^2 &=& (\mathbb{x}-\mathbb{\mu})^T\mathbb{\Sigma}^{-1}(\mathbb{x}-\mathbb{\mu}) \end{array} \end{equation}$$

概率相等的点分布在一个 $\mathbb{x}$ 空间的曲面上。 需要注意的是 $\Sigma$ 是一个对称矩阵，那么其特征向量形成一个正交向量集

$$\begin{equation} \begin{array}{rcl} \Sigma\mathbb{u}_i &=& \lambda_i\mathbb{u}_i \\ \mathbb{u}_i^T\mathbb{u}_j &=& I_{ij} \\ \Rightarrow \Sigma &=& \sum_{i=1}^D\lambda_i\mathbb{u}_i^T\mathbb{u}_i \\ \Rightarrow \Sigma^{-1} &=& \sum_{i=1}^D\frac{1}{\lambda_i}\mathbb{u}_i\mathbb{u}_i^T \\ \overset{y_i=\mathbb{u}_i^T(\mathbb{x}-\mathbb{\mu})}\Rightarrow \Delta^2 &=& \sum_{i=1}^D\frac{y_i^2}{\lambda_i} \\ \overset{\mathbb{y}=(y_1,\dots,y_D)^T}\Rightarrow\mathbb{y} &=& \mathbb{U}(\mathbb{x}-\mathbb{\mu}) \end{array} \end{equation}$$
其中: $\mathbb{U}$ 第i行为 $\mathbb{u}_i^T$， $\mathbb{U}^T\mathbb{U}=\mathbb{I}$

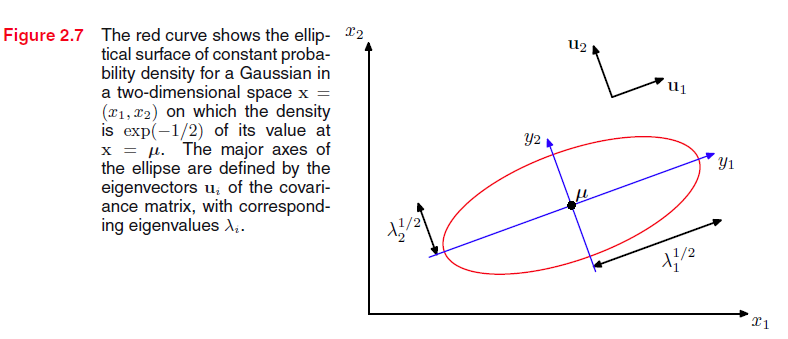
对于当前的高斯分布，协方差矩阵的特征值 $\lambda_i$ 必须严格正(全部大于0)，否则不能够合适地规范化，之后我们可能会遇到有些特征值为0的高斯分布，这些分布能够限制在更低的维度空间上。

之前我们考虑的是高斯分布的几何形态，由第一章p18我们知道 $p(y)=p_x(g(y))|g'(y)|,x=g(y)$，那么先求高斯分布 $x$ 关于 $y$ 的导数

$$\begin{equation} \begin{array}{rcl} y_i &=& \mathbb{u}_i^T(\mathbb{x}-\mathbb{\mu}) \\ J_{ij} &=& \frac{\partial{x_i}}{\partial{x_j}} = U_{ij} \\ |\mathbb{J}|^2 &=& |\mathbb{U}^T\mathbb{U}|=|\mathbb{I}|=1 \end{array} \end{equation}$$
而对称矩阵的行列式等于其特征值的连乘： $|\Sigma|^{1/2}=\prod_{j=1}^D\lambda_j^{1/2}$，那么
$$\begin{equation} \begin{array}{rcl} p(\mathbb{y}) &=& p(\mathbb{x})|\mathbb{J}|=\prod_{j=1}^D\frac{1}{\sqrt{2\pi\lambda_j}}\exp\{-\frac{y_j^2}{2\lambda_j} \} \end{array} \end{equation}$$

多元高斯分布的期望与协方差

$$\begin{equation} \begin{array}{rcl} E[\mathbb{x}] &=& \frac{1}{(2\pi)^{D/2 }|\mathbb{\Sigma}|^{1/2} } \int{\mathbb{x}\exp\{-\frac{1}{2}(\mathbb{x}-\mathbb{\mu})^T\Sigma^{-1}(\mathbb{x}-\mathbb{\mu})\}}d\mathbb{x} \\ &\overset{\mathbb{z}=\mathbb{x}-\mathbb{\mu}}=& \frac{1}{(2\pi)^{D/2 }|\mathbb{\Sigma}|^{1/2} } \int{(\mathbb{z}+\mathbb{\mu})\exp\{-\frac{1}{2}\mathbb{z}^T\Sigma^{-1}\mathbb{z}\}}d\mathbb{z} \\ &\overset{odd}=&\frac{1}{(2\pi)^{D/2 }|\mathbb{\Sigma}|^{1/2} } \int{\mathbb{\mu}\exp\{-\frac{1}{2}\mathbb{z}^T\Sigma^{-1}\mathbb{z}\}}d\mathbb{z} \\ &=& \mathbb{\mu} \\ E[\mathbb{x}\mathbb{x}^T] &=& \frac{1}{(2\pi)^{D/2 }|\mathbb{\Sigma}|^{1/2} } \int{\mathbb{x}\mathbb{x}^T\exp\{-\frac{1}{2}(\mathbb{x}-\mathbb{\mu})^T\Sigma^{-1}(\mathbb{x}-\mathbb{\mu})\}}d\mathbb{x} \\ &\overset{\mathbb{z}=\mathbb{x}-\mathbb{\mu}}=& \frac{1}{(2\pi)^{D/2 }|\mathbb{\Sigma}|^{1/2} } \int{(\mathbb{z}+\mathbb{\mu})(\mathbb{z}+\mathbb{\mu})^T\exp\{-\frac{1}{2}\mathbb{z}^T\Sigma^{-1}\mathbb{z}\}}d\mathbb{z} \\ &\overset{odd}=&\frac{1}{(2\pi)^{D/2 }|\mathbb{\Sigma}|^{1/2} } \int{(\mathbb{\mu}\mathbb{\mu}^T+\mathbb{z}\mathbb{z}^T)\exp\{-\frac{1}{2}\mathbb{z}^T\Sigma^{-1}\mathbb{z}\}}d\mathbb{z} \\ &=& \mathbb{\mu}\mathbb{\mu}^T+\frac{1}{(2\pi)^{D/2 }|\mathbb{\Sigma}|^{1/2} } \int{\mathbb{z}\mathbb{z}^T\exp\{-\frac{1}{2}\mathbb{z}^T\Sigma^{-1}\mathbb{z}\}}d\mathbb{z} \\ &\overset{y_i=\mathbb{u_i}^T\mathbb{z}}=& \mathbb{\mu}\mathbb{\mu}^T+\frac{1}{(2\pi)^{D/2 }|\mathbb{\Sigma}|^{1/2} } \sum_{i=1}^D\sum_{j=1}^D \mathbb{u}_i\mathbb{u}_j^T\int{\exp\{-\sum_{k=1}^D\frac{y_k^2}{2\lambda_k}\}}y_iy_jd\mathbb{y} \\ &=& \mathbb{\mu}\mathbb{\mu}^T+\sum_{i=1}^D\lambda_i\mathbb{u}_i\mathbb{u}_i^T \\ &=& \mathbb{\mu}\mathbb{\mu}^T+\Sigma \\ cov[\mathbb{x}] &=& E[(\mathbb{x}-E[\mathbb{x}])(\mathbb{x}-E[\mathbb{x}])^T]\\ &=& \Sigma \end{array} \end{equation}$$
$\mathbb{\mu},\Sigma$共同控制了高斯分布的形态，在D维空间中，一般情况下， $\mathbb{\mu}$ 有D个参数，而 $\Sigma$ 有 $D(D+1)/2$ 个参数(对称矩阵)，那么为了决定一个高斯分布的形态我们要有 $D(D+3)/2$ 个参数。对于低维空间来说这个参数是可以接受的；但是对于非常大的 $D$，计算量就会变得十分昂贵(协方差的逆矩阵)。

一个方法是限制协方差矩阵的形态：1. $\Sigma=diag(\sigma_i^2)$，此时只有 $2D$ 个参数；2. $\Sigma=\sigma^2\mathbb{I}$，此时有 $D+1$ 个参数。

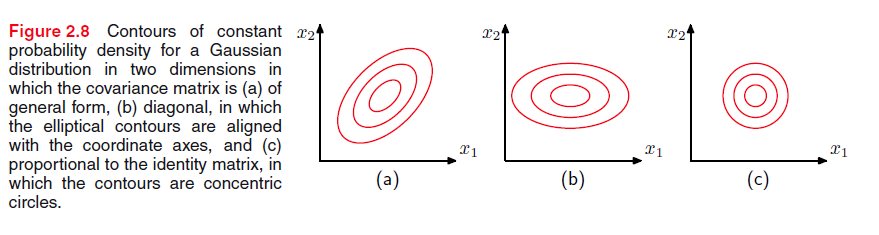
由上图知道，虽然限制协方差矩阵的形态能够使计算协方差矩阵的逆更加快速，但是这也限制了高斯函数的分布从而影响高斯分布拟合数据的能力。

条件高斯分布与边缘高斯分布

条件高斯分布与边缘高斯分布的推导可以参考PRML p86。

$$\begin{equation} \begin{array}{rcl} \mathbb{x} &=& \begin{pmatrix} \mathbb{x}_a \\ \mathbb{x}_b \end{pmatrix} \\ \mathbb{\mu} &=& \begin{pmatrix} \mathbb{\mu}_a \\ \mathbb{\mu}_b \end{pmatrix} \\ \mathbb{\Sigma} &=& \begin{pmatrix} \mathbb{\Sigma}_{aa} & \mathbb{\Sigma}_{ab} \\ \mathbb{\Sigma}_{ba} &\mathbb{\Sigma}_{bb} \end{pmatrix} \\ \mathbb{\Lambda} &=& \begin{pmatrix} \mathbb{\Lambda}_{aa} & \mathbb{\Lambda}_{ab} \\ \mathbb{\Lambda}_{ba} &\mathbb{\Lambda}_{bb} \end{pmatrix} \\ \end{array} \end{equation}$$

$p(\mathbb{x}) = p(\mathbb{x}_a,\mathbb{x}_b)$，当我们固定 $\mathbb{x}_b$ 就得到 $\mathbb{x}_a$ 关于 $\mathbb{x}_b$ 的条件概率

$$\begin{equation} \begin{array}{rcl} -\frac{1}{2}(\mathbb{x}-\mathbb{\mu})^T\mathbb{\Sigma}^{-1}(\mathbb{x}-\mathbb{\mu}) &=& -\frac{1}{2}(\mathbb{x}_a-\mathbb{\mu}_a)^T\mathbb{\Lambda}_{aa}(\mathbb{x}_a-\mathbb{\mu}_a) \\ && -\frac{1}{2}(\mathbb{x}_a-\mathbb{\mu}_a)^T\mathbb{\Lambda}_{ab}(\mathbb{x}_b-\mathbb{\mu}_b) \\ &&-\frac{1}{2}(\mathbb{x}_b-\mathbb{\mu}_b)^T\mathbb{\Lambda}_{ba}(\mathbb{x}_a-\mathbb{\mu}_a) \\ &&-\frac{1}{2}(\mathbb{x}_b-\mathbb{\mu}_b)^T\mathbb{\Lambda}_{bb}(\mathbb{x}_b-\mathbb{\mu}_b) \end{array} \end{equation}$$

由上面的推导我们知道，当 $\mathbb{x}_b$ 固定时，上式是关于 $\mathbb{x}_a$ 的二项式，因此 $p(\mathbb{x}_a|\mathbb{x}_b)$ 是干死分布。下面介绍知道一个高斯分布的指数的二项式之后，求它的期望与协方差矩阵。

$$\begin{equation} \begin{array}{rcl} -\frac{1}{2}(\mathbb{x}-\mathbb{\mu})^T\mathbb{\Sigma}^{-1}(\mathbb{x}-\mathbb{\mu}) &=& -\frac{1}{2}\mathbb{x}^T\Sigma^{-1}\mathbb{x}+\mathbb{x}^T\Sigma^{-1}\mathbb{\mu}+const \end{array} \end{equation}$$

上式的const是指与 $\mathbb{x}$ 无关的项。根据上式我们就得到 $p(\mathbb{x}_a|\mathbb{x}_b)$ 的均值与协方差矩阵

$$\begin{equation} \begin{array}{rcl} -\frac{1}{2}(\mathbb{x}-\mathbb{\mu})^T\mathbb{\Sigma}^{-1}(\mathbb{x}-\mathbb{\mu}) &=& -\frac{1}{2}(\mathbb{x}_a-\mathbb{\mu}_a)^T\mathbb{\Lambda}_{aa}(\mathbb{x}_a-\mathbb{\mu}_a) \\ && -\frac{1}{2}(\mathbb{x}_a-\mathbb{\mu}_a)^T\mathbb{\Lambda}_{ab}(\mathbb{x}_b-\mathbb{\mu}_b) \\ &&-\frac{1}{2}(\mathbb{x}_b-\mathbb{\mu}_b)^T\mathbb{\Lambda}_{ba}(\mathbb{x}_a-\mathbb{\mu}_a) \\ &&-\frac{1}{2}(\mathbb{x}_b-\mathbb{\mu}_b)^T\mathbb{\Lambda}_{bb}(\mathbb{x}_b-\mathbb{\mu}_b) \\ &=& -\frac{1}{2}\mathbb{x}_a^T\Lambda_{aa}\mathbb{x}_a+\mathbb{x}_a^T(\Lambda_{aa}\mathbb{\mu}_{aa}-\Lambda_{ab}(\mathbb{x}_b-\mathbb{\mu}_b))+const \\ \Rightarrow \Sigma_{a|b}^{-1} &=& \Lambda_{aa} \\ \Rightarrow \Sigma_{a|b}^{-1}\mathbb{\mu}_{a|b} &=& \Lambda_{aa}\mathbb{\mu}_{aa}-\Lambda_{ab}(\mathbb{x}_b-\mathbb{\mu}_b) \\ \Rightarrow \mathbb{\mu}_{a|b} &=& \mathbb{\mu}_{aa}-\Lambda_{aa}^{-1}\Lambda_{ab}(\mathbb{x}_b-\mathbb{\mu}_b) \end{array} \end{equation}$$

条件高斯分布 $p(\mathbb{x}_a|\mathbb{x}_b)$ 的均值是 $\mathbb{x}_b$ 的线性函数

至于边缘函数则可以由积分求得: $p(\mathbb{x}_a)=\int{p(\mathbb{x}_a,\mathbb{x}_b)}d\mathbb{x}_b$，与条件高斯分布的推导基本类似都是，详细请看书P88，下面只给出结果

$$\begin{equation} \begin{array}{rcl} E[\mathbb{x}_a] &=& \mathbb{\mu}_a \\ cov[\mathbb{x}_a] &=& \Sigma_{aa} \end{array} \end{equation}$$

高斯条件分布 $p(\mathbb{y}|\mathbb{x})$ 的均值是 $\mathbb{x}$ 的线性函数那么，

$$\begin{equation} \begin{array}{rcl} p(\mathbb{x}) &=& \mathcal{N}(\mathbb{x}|\mathbb{\mu},\Lambda^{-1}) \\ p(\mathbb{y}|\mathbb{x}) &=& \mathcal{N}(\mathbb{y}|\mathbb{A}\mathbb{x}+\mathbb{b},L^{-1}) \\ \Rightarrow p(\mathbb{y}) &=& \mathcal{N}(\mathbb{y}|\mathbb{A}\mathbb{\mu}+\mathbb{b},L^{-1}+\mathbb{A}\Lambda^{-1}\mathbb{A}^T) \\ \Rightarrow p(\mathbb{x}|\mathbb{y}) &=& \mathcal{N}(\mathbb{y}|\Sigma\{\mathbb{A}^TL(\mathbb{y}-\mathbb{b})+\Lambda\mathbb{\mu} \},\Sigma) \\ \Sigma &=& (\Sigma+\mathbb{A}L\mathbb{A})^{-1} \end{array} \end{equation}$$

需要注意的是，书中的推导是先求出 $p(\mathbb{x},\mathbb{y})$ ，然后再根据高斯条件分布与高斯边缘分布的结论直接得出 $p(\mathbb{y}),p(\mathbb{x}|\mathbb{y})$

高斯分布的最大似然

$\mathbb{X}=\{\mathbb{x}_1,\dots,\mathbb{x}_N\},\{\mathbb{x}_n\}$ 独立同分布。

$$\begin{equation} \begin{array}{rcl} \ln{p(\mathbb{X}|\mathbb{\mu},\mathbb{\Sigma})} &=& -\frac{ND}{2}\ln(2\pi)-\frac{N}{2}\ln|\Sigma|+\frac{1}{2}\sum_{n=1}^N(\mathbb{x}_n-\mathbb{\mu})^T\Sigma^{-1}(\mathbb{x}_n-\mathbb{\mu}) \\ \overset{\frac{\partial{\ln p}}{\partial\mathbb{\mu}}=0}\Rightarrow 0 &=& -\frac{1}{2}\sum_{n=1}^T\{\Sigma^{-1}(\mathbb{x}_n-\mathbb{\mu})+\{(\mathbb{x}_n-\mathbb{\mu})\Sigma^{-1}\}^T\} \\ \Rightarrow \mathbb{\mu}_{ML} &=& \frac{1}{N}\sum_{n=1}^N\mathbb{x}_n \\ \overset{\frac{\partial{\ln p}}{\partial{\Sigma}}=0}\Rightarrow 0 &=& -\frac{N}{2}\Sigma^{-1}-\frac{1}{2}\sum_{n=1}^T\{(\mathbb{x}_n-\mathbb{\mu})(\mathbb{x}_n-\mathbb{\mu})^T(-\Sigma^{-2})\} \\ \Rightarrow \Sigma_{ML} &=& \frac{1}{N}\sum_{n=1}^N(\mathbb{x}_n-\mathbb{\mu}_{ML})(\mathbb{x}_n-\mathbb{\mu}_{ML})^T \\ \end{array} \end{equation}$$

由于 $\mathbb{\mu}_{ML}$ 不依赖于 $\Sigma_{ML}$ ，可以先求 $\mathbb{\mu}_{ML}$ 再求 $\Sigma_{ML}$。

$$\begin{equation} \begin{array}{rcl} E[\mathbb{\mu}_{ML}] &=& E[\frac{1}{N}\sum_{n=1}^N\mathbb{x}_{n}] \\ p(x,y)=p(x)p(y) &\Rightarrow& E[x+y]=E[x]+E[y] \\ E[\mathbb{\mu}_{ML}] &=& \frac{1}{N}\sum_{n=1}^NE[\mathbb{x}_n] = \mathbb{\mu} \\ p(x_m,x_n)=p(x_n)p(x_m),p(x)\sim N(x|\mu,\sigma^2) &\Rightarrow& E[x_nx_m]=\mu^2+\sigma^2I_{nm} \\ E[\Sigma_{ML}] &=& \frac{N-1}{N}\Sigma \end{array} \end{equation}$$

顺序估计(sequential estimation)

首先对于高斯分布的均值(mean)估计：$\mathbb{\mu}_{ML} = \frac{1}{N}\sum_{n=1}^N\mathbb{x}_n$

$$\begin{equation} \begin{array}{rcl} \mathbb{\mu}_{ML}^N &=& \frac{1}{N}\sum_{n=1}^N\mathbb{x}_n \\ &=& \frac{1}{N}\mathbb{x}_N+\frac{1}{N}\sum_{n=1}^{N-1}\mathbb{x}_n \\ &=& \frac{1}{N}\mathbb{x}_N+\frac{N-1}{N}\mathbb{\mu}_{ML}^{N-1} \\ &=& \mathbb{\mu}_{ML}^{N-1}+\frac{1}{N}(\mathbb{x}_N-\mathbb{\mu}_{ML}^{N-1} )\\ \end{array} \end{equation}$$

在我们估计了 $N-1$ 个观测值的 $\mathbb{\mu}_{ML}^{N-1}$ 后又来了一个新的观测数据，我们能够很轻松的利用先前的 $\mathbb{\mu}_{ML}^{N-1}$ 来估计 $\mathbb{\mu}_{ML}^{N}$，大大减小了计算量。对于拥有 $\mathbb{\mu}_{ML}\propto \sum_{n=1}^N\mathbb{x}_n$，我们可以利用上式来进行sequential estimation。如果更一般的话，我们可以利用Robbins-Monro算法推导更一般的形式

$$\theta^{(N)}=\theta^{(N-1)}+a_{N-1}\frac{\partial{}}{\partial{\theta^{(N-1)}}}\ln{p(x_N|\theta^{(N-1)})}$$
如单一变量的高斯分布， $\frac{\partial{}}{\partial{\mu_{ML}}}\ln{p(x|\mu_{ML},\sigma^2)}=\frac{1}{\sigma^2}(x-\mu_{ML})$，此时令 $a_{N}=\sigma^2/N$

高斯分布的贝叶斯推理

前面我们大致介绍了在贝叶斯推理中，最重要的是选择共轭先验。在高斯分布中，共轭先验的选择相对于多项分布更复杂，主要分为以下三种情况，先考虑单一变量的高斯分布
1 $\sigma^2$ 已知，$\mu$ 未知：取高斯分布作为先验 $\mathcal{N}(\mu|\mu_0,\sigma^2)$
2 $\sigma^2$ 未知，$\mu$ 已知：取伽马分布作为先验

$$\begin{equation} \begin{array}{rcl} Gam(\lambda|a,b) &=& \frac{1}{\Gamma(a)}b^a\lambda^{a-1}\exp(-b\lambda)\\ E[\lambda] &=& \frac{a}{b}\\ var[\lambda] &=& \frac{a}{b^2} \end{array} \end{equation}$$

3 当 $\sigma^2,\mu$ 都未知，取Normal-Gamma分布做为先验

$$\begin{equation} \begin{array}{rcl} p(\mu,\lambda) &=& \mathcal{N}(\mu|\mu_0,(\beta\lambda)^{-1})Gam(\lambda|a,b) \\ \end{array} \end{equation}$$

共轭先验的选取主要是考察似然函数的形式，这个推导就不详细叙述。对于D维变量的高斯分布的共轭先验，大致与单一变量的高斯分布一样
1 $\Lambda$ 已知，$\mathbb{\mu}$ 未知：取高斯分布作为先验 $\mathcal{N}(\mathbb{\mu}|\mathbb{\mu_0},\Lambda)$

2 $\Lambda$ 未知，$\mu$ 已知：取Wishart分布作为先验

$$\begin{equation} \begin{array}{rcl} \mathcal{W}(\Lambda|\mathbb{W},\nu) &=& B|\Lambda|^{(\nu-D-1)/2}\exp(-\frac{1}{2}Tr(\mathbb{W}^{-1}\Lambda ))\\ B(\mathbb{W},\nu) &=& |\mathbb{W}|^{-\nu/2}(2^{\nu D/2}\pi^{D(D-1)/4}\prod_{i=1}^D\Gamma(\frac{\nu+1-i}{2}))^{-1} \end{array} \end{equation}$$

3 当 $\Lambda,\mu$ 都未知，取Normal-Wishart分布做为先验

$$\begin{equation} \begin{array}{rcl} p(\mu,\lambda) &=& \mathcal{N}(\mu|\mu_0,(\beta\Lambda)^{-1})\mathcal{W}(\Lambda|\mathbb{W},\nu) \\ \end{array} \end{equation}$$

Student’s t-distribution

$$\begin{equation} \begin{array}{rcl} p(x|\mu,a,b)&=&\int_0^\infty{\mathcal{N}(x|\mu,\tau^{-1})Gam(\tau|a,b) }d\tau] \\ \Rightarrow St(x|\mu,\lambda,\nu) &=& \frac{\Gamma(\nu/2+1/2)}{\Gamma(\nu/2)}(\frac{\lambda}{\pi\nu})^{1/2}[1+\frac{\lambda(x-\mu)^2}{\nu}]^{-\nu/2-1/2} \\ \end{array} \end{equation}$$

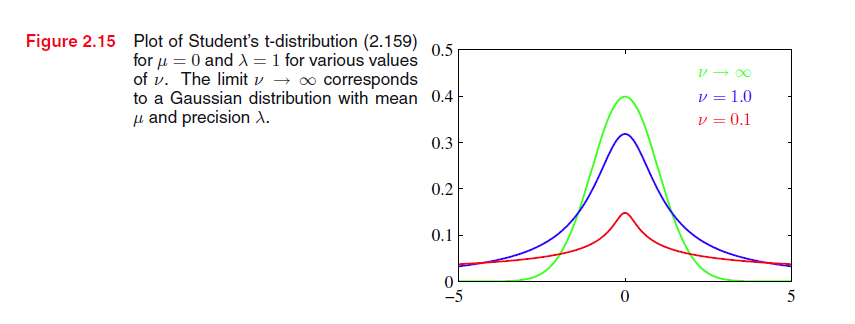
t-分布是由无穷个具有相同 $\mu$ 不同 $\lambda$ 的高斯分布累加而成的，t-分布比高斯分布具有更长的尾巴，从而使其对离群点更加鲁棒。

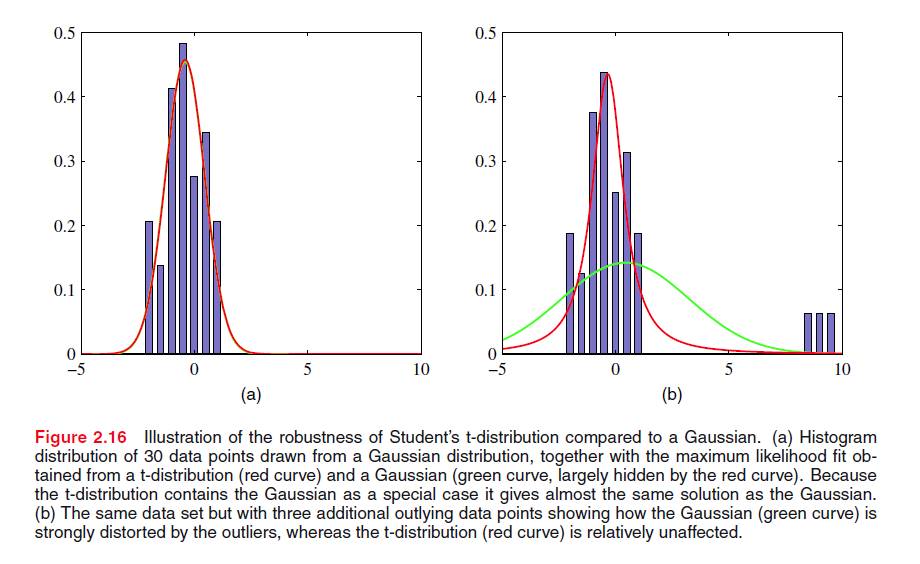
当 $\nu\to\infty$ 时，t-分布就变成了 $\mathcal{N}(x|\mu,\lambda^{-1})$

$$\begin{equation} \begin{array}{rcl} St(\mathbb{x}|\mathbb{\mu},\Lambda,\nu) &=& \frac{\Gamma(\nu/2+D/2)}{\Gamma(\nu/2)}(\frac{|\Lambda|^{1/2}}{(\pi\nu)^{D/2}})[1+\frac{\Delta^2}{\nu}]^{-\nu/2-D/2} \\ \Delta^2 &=& (\mathbb{x}-\mathbb{\mu})^T\Lambda(\mathbb{x}-\mathbb{\mu}) \\ E[\mathbb{x}] &=& \mathbb{\mu}, ~~~~~~~~~~~~~~~~~if ~~~~\nu>1 \\ cov[\mathbb{x}] &=& \frac{\nu}{\nu-2}\Lambda^{-1},~~if~~~~\nu>2 \\ mode[\mathbb{x}] &=& \mathbb{\mu} \end{array} \end{equation}$$

周期变量

从笛卡尔坐标系转到极坐标系。von Mises分布

$$\begin{equation} \begin{array}{rcl} p(\theta|\theta_0,m) &=& \frac{1}{2\pi I_0(m)}\exp(m\cos(\theta-\theta_0)) \\ I_0(m) &=& \frac{1}{2\pi}\int_0^{2\pi}{\exp(m\cos\theta) }d\theta \end{array} \end{equation}$$

混合高斯(Mixtures of Gaussians)

我们知道高斯分布是一个单峰分布，对于实际应用如果用单一高斯分布会存在很大的限制

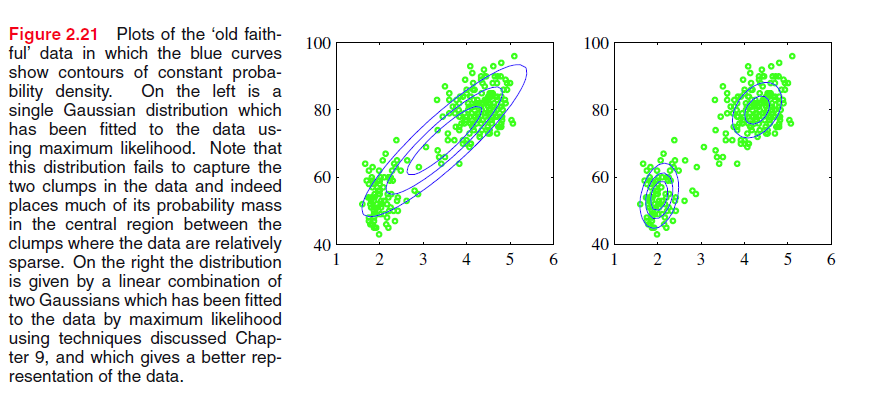
上图中的左子图明显不能捕捉到数据的真实分布，我们希望能得到右子图的模型。因此提出混合高斯模型

$$\begin{equation} \begin{array}{rcl} p(\mathbb{x}) &=& \sum_{k=1}^K\pi_k\mathcal{N}(\mathbb{x}|\mathbb{\mu}_k,\Sigma_k) \\ \sum_{k=1}^K\pi_k &=& 1 \end{array} \end{equation}$$

下图是3个高斯分布的混合模型

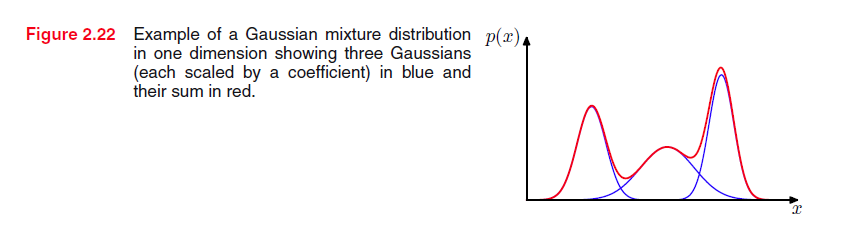
假如我们将混合系数 $\pi_k$ 泛化

$$\begin{equation} \begin{array}{rcl} p(\mathbb{x}) &=& \sum_{k=1}^Kp(k)p(\mathbb{x}|k) \\ \gamma_k(\mathbb{x}) &\equiv& p(k|\mathbb{x}) =\frac{p(k)p(\mathbb{x}|k)}{\sum_lp(l)p(\mathbb{x}|l)} \end{array} \end{equation}$$

对混合高斯模型的最大化似然函数采用EM模型

指数族分布

加入一个分布满足以下条件，则称其属于指数族分布

$$\begin{equation} \begin{array}{rcl} p(\mathbb{x}|\boldsymbol{\eta}) &=& h(\mathbb{x})g(\boldsymbol{\eta})\exp\{\boldsymbol{\eta}^T\mathbb{u}(\mathbb{x})\} \\ 1 &=& \int h(\mathbb{x})g(\boldsymbol{\eta})\exp\{\boldsymbol{\eta}^T\mathbb{u}(\mathbb{x})\}d\mathbb{x} \end{array} \end{equation}$$

下面从指数族分布来考虑先前我们介绍过的一些分布

伯努利分布

$$\begin{equation} \begin{array}{rcl} p(x|\mu) &=& Bern(x|\mu) = \mu^x(1-\mu)^{(1-x)} \\ &=& \exp\{x\ln\mu+(1-x)\ln(1-u) \} \\ &=& (1-\mu)\exp\{x\ln\frac{\mu}{1-\mu} \} \\ \overset{\eta=\ln\frac{\mu}{1-\mu}}\Rightarrow \mu &=& \sigma(\eta)=\frac{1}{1+\exp(-\eta)} \\ \Rightarrow p(x|\eta) &=& \sigma(-\eta)\exp(\eta x) \end{array} \end{equation}$$

对照指数族分布的形式，我们有

$$\begin{equation} \begin{array}{rcl} u(x) &=& x \\ h(x) &=& 1 \\ g(\eta) &=& \sigma(-\eta) \end{array} \end{equation}$$

这就是为什么我在二分类的逻辑回归问题中我们用logistics sigmoid function的原因。

多项式分布

$$\begin{equation} \begin{array}{rcl} p(\mathbb{x}|\mathbb{\mu}) &=& \prod_{k=1}^K\mu_k^{x_k} = \exp\{\sum_{k=1}^Kx_k\ln\mu_k \} \\ \overset{\eta_k=\ln\mu_k}\Rightarrow p(\mathbb{x}|\boldsymbol\eta) &=& \exp(\boldsymbol{\eta}^T\mathbb{x}) \\ u(x) &=& x \\ h(x) &=& 1 \\ g(\eta) &=& 1 \end{array} \end{equation}$$

我们知道 $\eta_k$ 不是独立的，因为 $\sum_{k=1}^K\mu_k=1$，加入我们只保留 $K-1$ 个参数，那么就会得到类似伯努利分布的指数形态。

$$\begin{equation} \begin{array}{rcl} \exp\{\sum_{k=1}^Kx_k\ln\mu_k \} &=& \exp\{\sum_{k=1}^{K-1}x_k\ln\mu_k+(1-\sum_{k=1}^{K-1}x_k)\ln(1-\sum_{k=1}^{K-1}\mu_k) \} \\ &=& \exp\{\sum_{k=1}^{K-1}x_k\ln{\frac{\mu_k}{1-\sum_{k=1}^{K-1}\mu_k} }+\ln(1-\sum_{k=1}^{K-1}\mu_k) \} \\ \overset{\eta_k=\ln{\frac{\mu_k}{1-\sum_{k=1}^{K-1}\mu_k} }}\Rightarrow \mu_k &=& \frac{\exp(\eta_k)}{1+\sum_{j=1}^{K-1}\exp(\eta_j)}\\ p(\mathbb{x}|\boldsymbol\eta) &=& (1+\sum_{j=1}^{K-1}\exp(\eta_j))^{-1}\exp(\boldsymbol{\eta}^T\mathbb{x}) \\ u(x) &=& x \\ h(x) &=& 1 \\ g(\eta) &=& (1+\sum_{j=1}^{K-1}\exp(\eta_j))^{-1} \end{array} \end{equation}$$

$\mu_k = \frac{\exp(\eta_k)}{1+\sum_{j=1}^{K-1}\exp(\eta_j)}$ 即softmax函数。

高斯分布

$$\begin{equation} \begin{array}{rcl} p(x|\mu,\sigma^2) &=& \frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})\\ &=& \frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{x^2-2x\mu+\mu^2}{2\sigma^2}) \\ \boldsymbol{\eta} &=& \begin{pmatrix} \mu/\sigma^2 \\ -1/2\sigma^2 \end{pmatrix}\\ u(x) &=& \begin{pmatrix} x \\ x^2 \end{pmatrix} \\ h(x) &=& (2\pi)^{-1/2} \\ g(\eta) &=& (-2\eta_2)^{1/2}\exp(\frac{\eta_1^2}{4\eta_2}) \end{array} \end{equation}$$

指数族分布的最大似然

在介绍指数族分布的最大似然之前，我们先求一下指数族分布的真实 $\boldsymbol{\eta}$

$$\begin{equation} \begin{array}{rcl}\ \int h(\mathbb{x})g(\boldsymbol{\eta})\exp\{\boldsymbol{\eta}^T\mathbb{u}(\mathbb{x})\}d\mathbb{x} &=& 1 \end{array} \end{equation}$$

上式两边对 $\boldsymbol{\eta}$ 求导，得

$$\begin{equation} \begin{array}{rcl}\ \nabla g(\boldsymbol{\eta}) \int h(\mathbb{x})\exp\{\boldsymbol{\eta}^T\mathbb{u}(\mathbb{x})\}d\mathbb{x}+\int h(\mathbb{x})g(\boldsymbol{\eta})\exp\{\boldsymbol{\eta}^T\mathbb{u}(\mathbb{x})\}\mathbb{u}(\mathbb{x})d\mathbb{x} &=& 0 \\ \Rightarrow -\nabla\ln g(\boldsymbol{\eta}) = \int h(\mathbb{x})g(\boldsymbol{\eta})\exp\{\boldsymbol{\eta}^T\mathbb{u}(\mathbb{x})\}\mathbb{u}(\mathbb{x})d\mathbb{x} &=& \mathbb{E}[\mathbb{u}(\mathbb{x})] \end{array} \end{equation}$$

当 $\mathbb{X} = \{\mathbb{x}_1,\dots,\mathbb{x}_N \}, p(\mathbb{x}_n|\boldsymbol{\eta})=h(\mathbb{x}_n)g(\boldsymbol{\eta})\exp(\boldsymbol{\eta}^T\mathbb{u}(\mathbb{x})\}$，那么它的似然函数为

$$\begin{equation} \begin{array}{rcl} p(\mathbb{X}|\boldsymbol{\eta}) &=& \{\prod_{n=1}^Nh(\mathbb{x}_n)\}g(\boldsymbol{\eta})^N\exp\{\sum_{n=1}^N\{\boldsymbol{\eta}^T\mathbb{u}(\mathbb{x})\}\} \\ \overset{\frac{\partial{\ln p}}{\partial{\boldsymbol{\eta}} }=0 }\Rightarrow -\nabla\ln g(\boldsymbol{\eta}_{ML}) &=& \frac{1}{N}\sum_{n=1}^N\mathbb{u}(\mathbb{x}) \end{array} \end{equation}$$
从而当 $N\to\infty$时， $\boldsymbol{\eta}_{ML}$ 等于真实的 $\boldsymbol{\eta}$ 。

共轭先验

由似然函数的形式我们得到指数族的共轭先验

$$\begin{equation} \begin{array}{rcl} p(\boldsymbol{\eta}|\mathbb{\chi},\nu) &=& f(\mathbb{\chi},\nu)g(\boldsymbol{\eta})^{\nu}\exp\{\nu \boldsymbol{\eta}^T\mathbb{\chi} \} \end{array} \end{equation}$$

其中 $f(\mathbb{\chi},\nu)$ 是归一化系数

$$\begin{equation} \begin{array}{rcl} p(\boldsymbol{\eta}|\mathbb{X},\mathbb{\chi},\nu) &\propto& g(\boldsymbol{\eta})^{\nu+N}\exp\{\boldsymbol{\eta}^T(\sum_{n=1}^N\mathbb{x}_n+\nu \mathbb{\chi}) \} \end{array} \end{equation}$$

无信息(noninformative)先验

由于 $p(y|x)\propto p(x|y)p(y)$ ，如果先验在某些点上概率为0，就算我们之后观测到这些点，但是后验的概率也为0。而通常情况下，我们并不知道数据的概率分布函数，因此为解决上述问题，引入了noninformative prior。(也没太理解PRML这节的组织形式，先放着之后再看)

非参数(nonparametric)法

之前的概率分布都是一些具有特定形式的函数，并且能有少数的参数来控制这个函数的形态，但是采用这种方法会很大的局限性，因为我们选取的概率分布函数有可能不能捕捉数据的潜在概率分布。比如说高斯分布中，数据的潜在概率分布可能具有多个峰值，但是高斯分布是个单峰函数，因此在预测新的数据的时候，预测性能会很差，这种问题可以用混合高斯分布等扩展方法来解决。我们下面介绍另一个方法：非参数法。

假设观测值是从一个未知的概率分布 $p(\mathbb{x})$ 中选取的，$\mathbb{x}$ 是D维空间的点，那么对于一个很小的区域 $\mathcal{R}$ ，这个区域的概率质量为

$$\begin{equation} \begin{array}{rcl} P &=& \int_\mathcal{R}p(\mathbb{x})d\mathbb{x} \end{array} \end{equation}$$

现在假设我们从 $p(\mathbb{x})$ 中选取N个观测值，那么落在区域 $\mathcal{R}$ 的观测值个数 $K$ 服从二项分布

$$\begin{equation} \begin{array}{rcl} Bin(K|N,P) &=& \frac{N!}{K!(N-K)!}P^{K}(1-P)^{N-K} \\ E[K/N] &=& P &(E[K]=P)\\ var[K/N] &=& P(1-P)/N &(var[K]=NP(1-P)) \\ \end{array} \end{equation}$$

当N很大的时候，由 $var[K/N] = P(1-P)/N$ 知道分布会集中分布中均值上，此时的均值 $K\simeq NP$

当 $\mathcal{R}$ 足够小，那么在这个区域上 $p(\mathbb{x})$ 近似为一个常数，那么 $P\simeq p(\mathbb{x})V$。从而有 $p(\mathbb{x})=\frac{K}{NV}$ (两个假设，在实际应用中会不会导致结果相差太大?)。这个估计公式主要由 $K,V$ 两个值决定

核密度估计(kernel density estimation)

固定 $V$，从数据中决定 $K$。为了简化，我们使 $\mathcal{R}$ 是待估计值 $\mathbb{x}$ 上的边长为h超立方体(hypercube)在。当 $\mathbb{x}_n$ 与 $\mathbb{x}$ 满足一定条件时，$\mathbb{x}_n$ 就落在该超立方体里。我们介绍Parzen window

$$\begin{equation} \begin{array}{rcl} k(\mathbb{u}) &=& \begin{cases} 1,&|u_i|\le1/2,i=1,\dots,D, \\ 0,&otherwise \end{cases} \end{array} \end{equation}$$

我们取 $k((\mathbb{x}-\mathbb{x}_n)/h)$，那么 $K=\sum_{n=1}^Nk(\frac{\mathbb{x}-\mathbb{x}_n}{h})$，那么对于 $p(\mathbb{x})$，我们就得到

$$\begin{equation} \begin{array}{rcl} p(\mathbb{x}) &=& \frac{1}{Nh^D}\sum_{n=1}^Nk(\frac{\mathbb{x}-\mathbb{x}_n}{h}) \end{array} \end{equation}$$

Parzen window核函数会导致求出的 $p'(\mathbb{x})$ 人为的不连续性，而不是因为 $p(\mathbb{x})$ 本身引起的。因此采用另一个核函数——高斯核函数

$$\begin{equation} \begin{array}{rcl} p(\mathbb{x}) &=& \frac{1}{N\sqrt{2\pi h^2}}\sum_{n=1}^N \exp(-\frac{||\mathbb{x}-\mathbb{x}_n||^2}{2h^2}) \end{array} \end{equation}$$

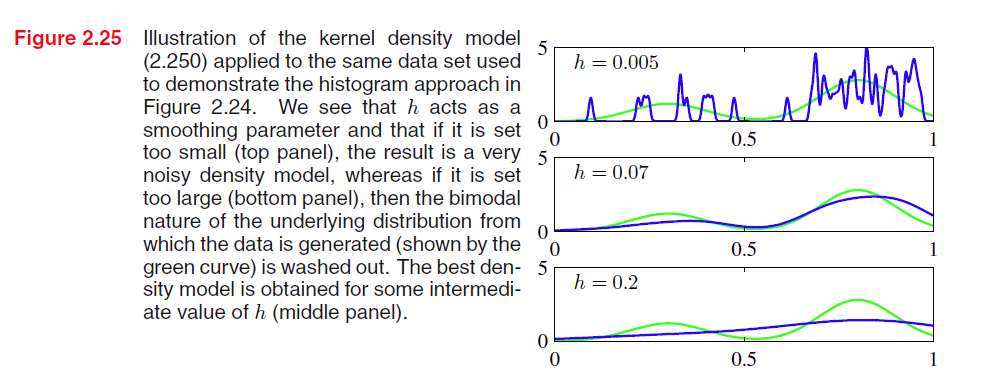
我们可以看到从现在的超参数就变成了 $h$ 。

最邻近法(Nearest-neighbour methods)

核方法的一个局限性是，它对于大部分空间上具有相同的密度，但是有些数据集可能在某些区域密度较为集中，而另一些区域密度相对较小，那么核方法中的 $h$ 就难以选择。此时我们考虑固定 $K$，而使用数据去找到合适的 $V$.

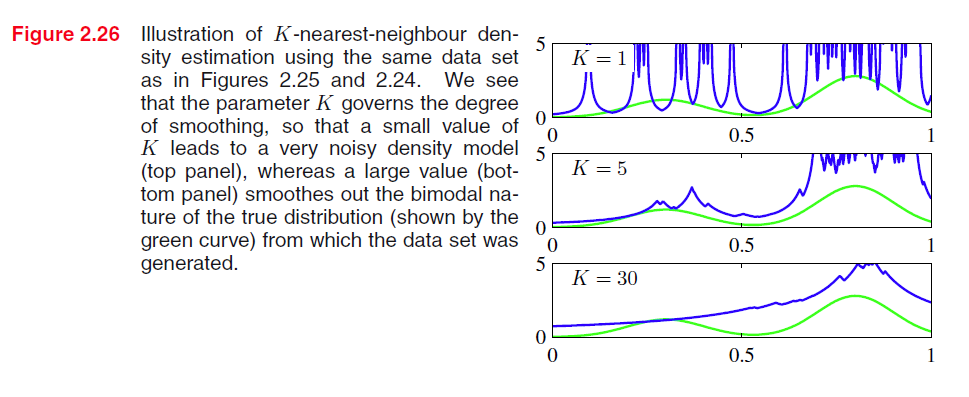
假设一个数据集一共有N个实例，其中有 $N_k$ 个属于类 $C_k$，$\sum_{k}N_k=N$。如果我们想分类一个新的实例 $\mathbb{x}$ ，我们以 $\mathbb{x}$ 为中心选取 $K$ 个实例。那么在这里面有 $K_k$ 个实例属于类 $C_k$。

$$\begin{equation} \begin{array}{rcl} p(\mathbb{x}|C_k) &=& \frac{K_k}{N_kV} \\ p(\mathbb{x}) &=& \frac{K}{NV} \\ p(C_k) &=& \frac{K_k}{N_k} \\ \Rightarrow p(C_k|\mathbb{x}) &=& \frac{p(\mathbb{x}|C_k)p(C_k)}{p(\mathbb{x})} = \frac{K_k}{K} \\ \end{array} \end{equation}$$
K-近邻算法的概率解释，通俗解释就是选取与测试实例最近的 $K$ 个实例，如果这 $K$ 个实例大多数都属于某个类 $C_k$，就讲测试实例分类到 $C_k$。

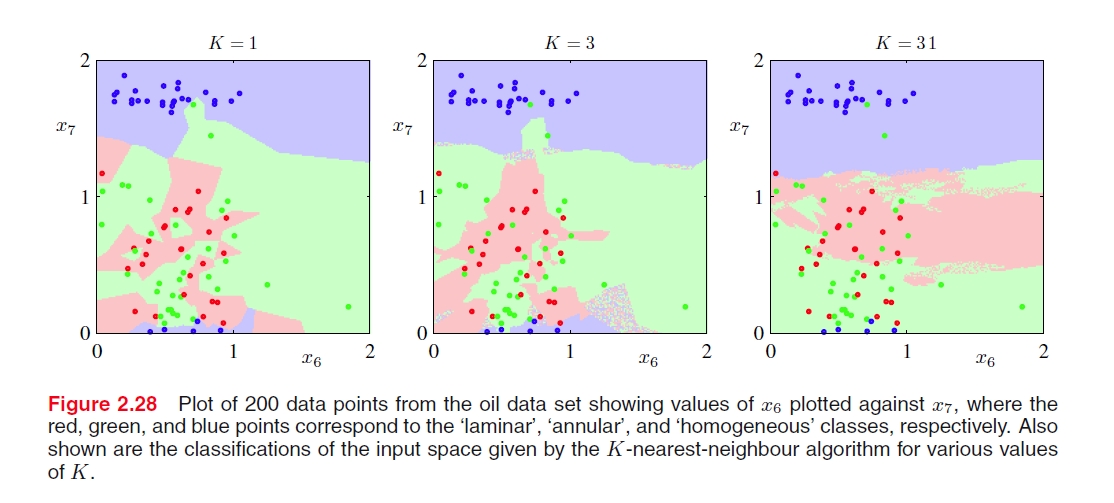
从上图的例子我们知道， K <script type="math/tex" id="MathJax-Element-422">K</script> 值选取会决定分类算法的性能。K-近邻算法需要保存整个数据集，当数据量很大时，计算十分昂贵，所以为了解决这个问题，可以构造树形搜索结构来加速计算。