PRML读书笔记(四)

分类的线性模型

分类的目标是在给定输入，预测具有离散性质的目标值。输入空间被多个决策平面划分成多个决策区域，每个区域代表一个类别。决策平面是输入特征的线性函数(待会会详细介绍)，因此在D维空间上的决策平面是(D-1)维的超平面，如果数据能够被这些决策平面准确划分成n个类别区域，那么数据集线性可分(linearly separable)。

当有K(>2)类时，我们采用 1-of-K 编码格式也叫one-hot encoding。 $\mathbb{t}=\{0,\dots,1,\dots,0\}^T,\sum_{k}t_k=1$。

生成模型与判别模型

这章的模型可以一般表示为

$$\begin{equation} \begin{array}{rcl} y(\mathbb{x}) &=& f(\mathbb{w}^T\phi(\mathbb{x})+w_0) \\ \end{array} \end{equation}$$

其中 $f(\cdot)$ 是激活函数。如果令 $f$ 为一个恒等函数(identity function)，即 $f(\cdot)=\cdot$，那么这个模型就变成了第三章的线性回归模型；而如果 $f$ 是非线性函数，那么这个模型就为分类模型，是一个广义线性模型(Generalized Linear Model,GLM)，这是因为决策平面为 $y(\mathbb{x})=\text{constant}\Rightarrow \mathbb{w}^T\phi(\mathbb{x})+w_0=\text{constant}$，可以看到决策平面是输入特征的线性函数。

4.1 判别函数(Discriminant Functions)

在给定输入特征时，判别函数输出一个类别 $\mathcal{C}_k$

4.1.1 二分类问题

最简单的判别函数为如下的线性判别函数

$$\begin{equation} \begin{array}{rcl} y(\mathbb{x}) &=& \mathbb{w}^T\mathbb{x}+w_0 \\ \end{array} \end{equation}$$

当 $y(\mathbb{x})\ge 0$ 时，我们将 $\mathbb{x}$ 分到类别 $\mathcal{C}_1$，否则分到 $\mathcal{C}_2$。因此bias项 $w_0$ 的负值有时候也被称为阈值。

因此决策平面 $\mathcal{S}$ 就并定义成了 $y(\mathbb{x})= 0$，从几何上看，我们可以知道 $\mathbb{w}^T$ 是 $\mathcal{S}$ 的法线，那么 $w_0$ 就可就决定了决策平面与原点的距离 $-\frac{w_0}{\|\mathbb{w}\|}$ 。

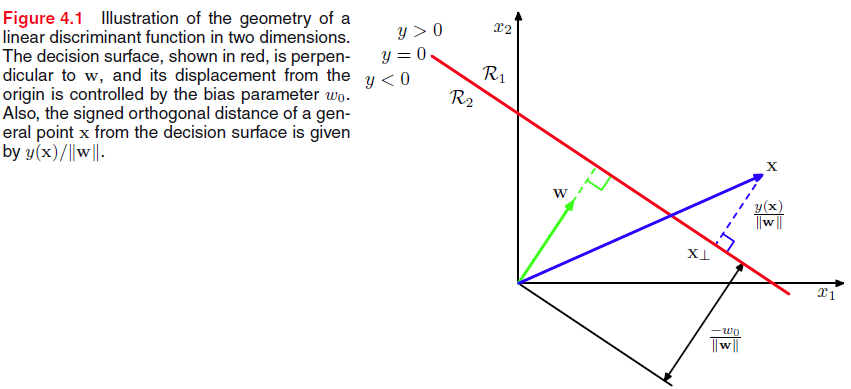
上图中 $\mathbb{x}$ 是空间上任意一点， $\mathbb{x_\bot}$ 是 $\mathbb{x}$ 正交投影到平面 $\mathcal{S}$ 上的点， $r$ 是 $\mathbb{x}$ 到 $\mathcal{S}$ 的距离，那么

$$\begin{equation} \begin{array}{rcl} \mathbb{x} &=& \mathbb{x_\bot}+r\frac{\mathbb{w}}{\|\mathbb{w}\|} \\ r &=& \frac{y(\mathbb{x})}{\|\mathbb{w}\|} \end{array} \end{equation}$$

如果令 $x_0=1,\tilde{\mathbb{w}}=\{w_0,\mathbb{w}\},\tilde{\mathbb{x}}=\{x_0,\mathbb{x}\}$，那么 $y(\mathbb{x})=\tilde{\mathbb{w}}^T\tilde{\mathbb{x}}$

4.1.2 多类别

对于多类别，可以训练K-1个分类器，每个分类器可以看做是一个二分类问题，即类别 $\mathcal{C}_k$ 与 非 $\mathcal{C}_k$，由于约束，我们训练K-1个分类器即可；训练 $K(K-1)/2$ 个分类器，类别为 $\mathcal{C}_k$ 和 $\mathcal{C}_j$。这两种方法都会导致模糊区域的问题

为了解决模糊区域问题，可以考虑 K 类别判别(K-class discriminant)，

$$\begin{equation} \begin{array}{rcl} y_k(\mathbb{x}) &=& \mathbb{w}_k^T\mathbb{x}+w_{k0} \end{array} \end{equation}$$

虽然形式上有点类似前两种方法，但是只有当所有 $j\neq k,y_k(\mathbb{x})>y_j(\mathbb{x})$ 时，才分类到 $\mathcal{C}_k$ ，那么 $\mathcal{C}_k$ 与 $\mathcal{C}_j$ 的决策边界(平面) 就变成了 $y_k(\mathbb{x})=y_j(\mathbb{x})\Rightarrow (\mathbb{w}_k-\mathbb{w}_j)^T\mathbb{x}+(w_{k0}-w_{j0})=0$，这与二分类的决策平面一致。

由上图知道 $\mathbb{x}_a,\mathbb{x}_b$ 是决策区域 $\mathcal{R}_k$ 的任意两个点，那么在直线 $\mathbb{x}_a\mathbb{x}_b$ 上的任一点 $\hat{\mathbb{x}}$ ，我们可以表示为

$$\begin{equation} \begin{array}{rcl} \hat{\mathbb{x}} &=& \lambda\mathbb{x}_a+(1-\lambda)\mathbb{x}_b ,0\leq\lambda\leq1\\ y_k(\hat{\mathbb{x}}) &=& \lambda y_k(\mathbb{x}_a)+(1-\lambda)y_k(\mathbb{x}_b) \end{array} \end{equation}$$

明显对于任意 $j\neq k$，我们有 $y_k(\hat{\mathbb{x}})\geq y_j(\hat{\mathbb{x}})$ ，即对于线性可分的数据，$\mathcal{R}_k$ 是单连通凸区域(singly connected and convex)。

4.1.3 分类的最小二乘法

采用最小二乘法能够使预测值逼近 $E[\mathbb{t} \vert \mathbb{x}]$，详细参考第三章中的最小二乘法的解释。 对于K类别，我们有

$$\begin{equation} \begin{array}{rcl} \mathbb{y}(\mathbb{x}) &=& \tilde{\boldsymbol{W}}^T\tilde{\mathbb{x}} \\ E_D(\tilde{\boldsymbol{W}}) &=& \frac{1}{2}Tr\left\{ (\tilde{\boldsymbol{X}}\tilde{\boldsymbol{W}}-\boldsymbol{T})^T(\tilde{\boldsymbol{X}}\tilde{\boldsymbol{W}}-\boldsymbol{T}) \right\} \\ \Rightarrow \tilde{\boldsymbol{W}} &=& (\tilde{\boldsymbol{X}}\tilde{\boldsymbol{X}})^{-1}\tilde{\boldsymbol{X}}^T\boldsymbol{T} \end{array} \end{equation}$$

最小二乘法对离群点不鲁棒，如下图

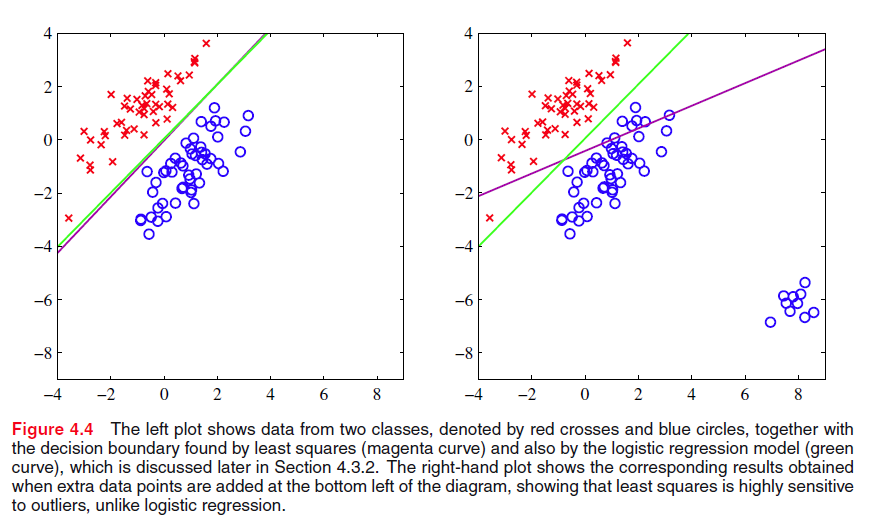
左图的决策边界已经能够很好地划分两个区域了，但是来了一些新的数据的时候，如右图，尽管原先的决策边界也能够很好地划分数据，但是由于采用了最小二乘法，为了使损失达到最小，即划分边界距离两个类的条件期望 $E[\mathbb{t} \vert \mathbb{x}]$ 最近，从而驱使原先的决策边界偏离，即右图紫色边界线。

(书上原话: The sum-of-squares error functin penalizes predictions that are ‘too correct’ in that they lie a long way on the correct side of descision boundary.)

我认为导致左图的原因除了二乘法原因外，还有 K-class discriminant方法中，所有的决策区域必定相交于一个平面，所以左图的数据对于 K-class discriminant是不可分的(?)

导致上述问题的一个根本原因是，最小二乘法是高斯分布假设下的最大似然估计解决方案，而对于分类问题的目标值是离散的，而不是连续的，从而与高斯分布假设不相符。

4.1.4 Fisher线性判别(Fisher’s linear discriminant)

线性判别函数一般表示为 $y=\mathbb{w}^T\mathbb{x}$， 从几何上看，我们将 D 为输入 $\mathbb{x}$ 经过一个变换之后，输出了一个一维的空间 $y$，并且在这个一维空间上不同类的数据是可分的。考虑2分类问题，只有推广。如果将每个类看成一个簇，那么它中点看做

$$\begin{equation} \begin{array}{rcl} \mathbb{m}_1=\frac{1}{N_1}\sum_{n\in\mathcal{C_1}}\mathbb{x}_n &,& \mathbb{m}_2=\frac{1}{N_2}\sum_{n\in\mathcal{C_2}}\mathbb{x}_n \end{array} \end{equation}$$

为了使不同类的数据分开，我们使 $\mathbb{m}_1,\mathbb{m}_2$ 投影到一维空间上的距离最远，即

$$\begin{equation} \begin{array}{rcl} m_2-m_1 = \mathbb{w}^T(\mathbb{m}_2-\mathbb{m}_1) \end{array} \end{equation}$$

假设 $\mathbb{x}_a\in\mathcal{C}_1$，当 $\mathbb{x}_a$ 在 $\mathbb{m}_1$ 附近或者 $\overrightarrow{m_1x_a}$ 的方向与 $\overrightarrow{m_1m_2}$ 背离(夹角大于90度)，那么 $\mathbb{x}_a$ 能够与 $\mathcal{C}_2$ 中的点很好地分离，同理 $\mathcal{C}_2$。
但是对于 $\mathbb{x}_a$ 不在 $\mathbb{m}_1$ 附近并且 $\overrightarrow{m_1x_a}$ 的方向与 $\overrightarrow{m_1m_2}$ 同向(不是夹角等于0，而是夹角小于90度) ，那么这些点就有可能不能很好地分离开，如下图左图所示

Fisher linear discriminant wiki。Fisher线性判别对这个问题进行了研究，他的思想要使类内(within-class)数据的方差最小，并且使类间(between-class)数据的方差最大，从而得出了Fisher criterion

J(w)s2k==(m2−m1)