AVL树详解（两种实现）

Duanzii

已于 2022-11-15 17:03:26 修改

阅读量615

点赞数 1

文章标签：数据结构算法

于 2022-11-10 22:34:57 首次发布

本文链接：https://blog.csdn.net/Lidystar/article/details/127598600

版权

一、AVL树的背景介绍

AVL树是最先发明的自平衡二叉查找树（Self-Balancing Binary Search Tree，简称平衡二叉树），它的名字来源于它的发明作者G.M. Adelson-Velsky 和 E.M. Landis。

二叉查找树的优势是缩短查找的效率，但如果数据有序或接近有序，二叉查找树将退化为单支树，查找元素相当于在顺序表中搜索元素，这样的效率非常低下。

因此这个时候，有两位俄罗斯的数学家 G.M.Adelson-Velsky 和 E.M.Landis 在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果对树中的结点进行调整，能保证每个结点的左右子树高度之差的绝对值不超过1，就可以降低树的高度，从而减少平均搜索长度。

于是，平衡二叉查找树诞生。

二、AVL树的概念

二叉查找树的定义：

一棵空树，或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；

（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

（4）没有键值相等的结点。

平衡二叉查找树（AVL）的定义：

一颗空树，或者是具有以下性质的二叉查找树：

（1）左子树和右子树的深度之差(平衡因子)的绝对值不超过1；

（2）左子树和右子树都是一颗平衡二叉树。

AVL树的特性就是让二叉查找树的节点实现平衡，节点相对均匀分布，而不是偏向某一侧。

三、AVL树的相关定义

1.节点的定义:

typedef struct AVLTreeNode
 {
     int data;
     int height;//节点的高度（也可以是bf,但这里是高度）
     struct BSTreeNode *lchild;//左子树
     struct BSTreeNode *rchild;//右子树
 }AVLTree;
或者
template<typename T>
class AVLTreeNode 
{
 public:
    T key;
    int height;
    AVLTreeNode *left;//左孩子
    AVLTreeNode *right;//右孩子
    AVLTreeNode(int key) 
    {
        this->key = key;
        this->height = 0;
        this->left = this->right = NULL;
    }
    ~AVLTreeNode() {}
};

*树的定义：

template<typename T>
class AVLTree {
public:
    AVLTreeNode<T> *root;
    AVLTree() 
    {
        this->root = NULL;
    }
    //获取树结点的高度
    int GetHeight(AVLTreeNode<T> *root);
    //更新树结点的高度
    int MaxHeight(AVLTreeNode<T> *root);
    //判断以他们分别作为根结点的子树的高度是否失去平衡，失去平衡返回true，否则返回false
    bool Check_Balance(AVLTreeNode<T> *a, AVLTreeNode<T> *b);

    //简称为LL旋转（LL的含义是左子树的左子树插入新结点）
    AVLTreeNode<T>* LeftLeftRotate(AVLTreeNode<T> *root);
    //简称为RR旋转（RR的含义是右子树的右子树插入新结点）
    AVLTreeNode<T>* RightRightRotate(AVLTreeNode<T> *root);
    //简称为LR旋转（LR的含义是左子树的右子树插入新节点）
    AVLTreeNode<T>* LeftRightRotate(AVLTreeNode<T> *root);
    //简称为RL旋转（RL的含义是右子树的左子树插入新节点）
    AVLTreeNode<T>* RightLeftRotate(AVLTreeNode<T> *root);

    //在AVL树中查找元素值为value的结点
    AVLTreeNode<T>* ValueFind(AVLTreeNode<T> *root,T value);
    //找到AVL树中元素值最小的结点，即树的最左边
    AVLTreeNode<T>* MinNode(AVLTreeNode<T> *root);
    //找到AVL树中元素值最大的结点，即树的最右边
    AVLTreeNode<T>* MaxNode(AVLTreeNode<T> *root);
    //在AVL树中插入元素值为T的结点
    AVLTreeNode<T>* InsetNode(AVLTreeNode<T> *root,T value);
    //删除结点
    AVLTreeNode<T>* DeleteNode(AVLTreeNode<T> *root, AVLTreeNode<T> *node);

    //先序遍历
    void PreOrder(AVLTreeNode<T> *root) 
    {
        if(root == NULL) return;
        std::cout<<root->key<<"->";
        PreOrder(root->left);
        PreOrder(root->right);
    }
    //中序遍历
    void InOrder(AvlNode<T> *root) 
    {
        if(root == NULL) return;
        InOrder(root->left);
        std::cout<<root->key<<"->";
        InOrder(root->right);
    }
    //后序遍历
    void PostOrder(AVLTreeNode<T> *root) 
    {
        if(root == NULL) return;
        PostOrder(root->left);
        PostOrder(root->right);
        std::cout<<root->key<<"->";
    }
};

class AVLTree
{
private:
    AVLTreeNode* root;        //根节点
public:
    /*构造函数*/
    AVLTree() :root(NULL) {};

    /*返回根节点*/
    AVLTreeNode* getRoot() { return root; }

    /*先序遍历*/
    void preOrder(AVLTreeNode* root);

    /*中序遍历*/
    void inOrder(AVLTreeNode* root);

    /*后序遍历*/
    void postOrder(AVLTreeNode* root);

    /*在AVL树root中查找值为key的结点并返回该结点*/
    AVLTreeNode* search(AVLTreeNode* root, int key);

    /*在AVL树中查找最小值结点并返回*/
    AVLTreeNode* minimus(AVLTreeNode* node);

    /*在AVL树中查找最大值结点并返回*/
    AVLTreeNode* maximus(AVLTreeNode* node);

    /*返回结点的高度*/
    int height(AVLTreeNode* node);

    /*左左旋转*/
    AVLTreeNode* leftLeftRotate(AVLTreeNode* root);

    /*右右旋转*/
    AVLTreeNode* rightRightRotate(AVLTreeNode* root);

    /*左右旋转*/
    AVLTreeNode* leftRightRotate(AVLTreeNode* root);

    /*右左旋转*/
    AVLTreeNode* rightLeftRotate(AVLTreeNode* root);

    /*插入结点*/
    AVLTreeNode* insert(AVLTreeNode* root, int key);

    /*删除结点node*/
    AVLTreeNode* deleteNode(AVLTreeNode* root, AVLTreeNode* node);

    /*销毁AVL树*/
    void destroy(AVLTreeNode* root);
};

2.深度：

从上往下数

节点的层次（节点的深度）：从根开始定义，根为第1层，根的子节点为第2层，以此类推；（这里说根节点为第1层，也可以说成根节点的深度为1。

树的深度：树中节点的最大层次

3.高度：

从下往上数

关于高度，空二叉树的高度为0，因为高度是从下往上数，所以叶子节点的高度为1，往上依次赠1。

在这里浅浅实现一下求节点的高度：传入一个二叉树的结点，然后我们返回这个二叉树结点的height成员变量，但是我们传入的结点可能是 NULL 直接去取元素的话会发生 RE 所以我们需要先判断一下。

int GetHeight(AVLTreeNode<T> *root)
{
    if (root != NULL) //若不为空子树
    {
        if (root->left == NULL && root->right == NULL) //若为叶子节点
        {
            return 1;    
        }
        else if (GetHeight(root->right) > GetHeight(root->left)) //若右子树高度较高
        {
            return (root->right)->height + 1;
        }
        else //若左子树高度较高
        {
            return (root->left)->height + 1;
        }
    }
    else //若为空子树
    {
        return 0;
    }
}

4.平衡因子：

将二叉树上节点的左子树高度减去右子树高度的值称为该节点的平衡因子BF(Balance Factor)。

简单来说，对于树的每一个分支节点，左右子树的高度差就为该节点的 平衡因子 ，显然对于每一个叶结点高度差为0。

对于平衡二叉树，BF的取值范围为[-1,1]，即-1,0,1。如果发现某个节点的BF值并不在此范围，则需要对树进行调整。

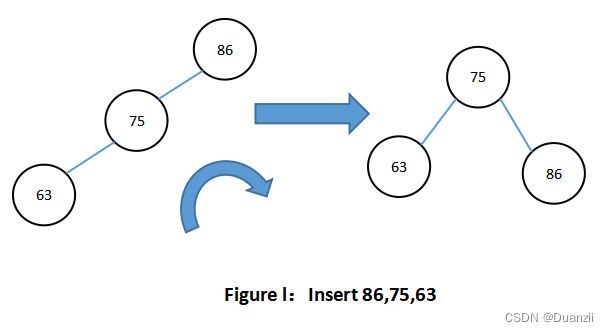
如图所示，左图中86的左右子树高度之差为2，即86这个节点的平衡因子为2，需要进行调整，调整后如右图，75的左右子树高度之差为0，即75这个节点的平衡因子为0。

四、AVL树的旋转（平衡调整）

1.LL型调整（右旋）:

由于在a的左孩子(L)的左子树(L)上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由1增至2。

下图是LL型的最简单形式。显然按照图中大小关系，节点B应作为新的根节点，其余两个节点分别作为左右孩子节点才能平衡，A结点就好像是绕节点B顺时针旋转一样。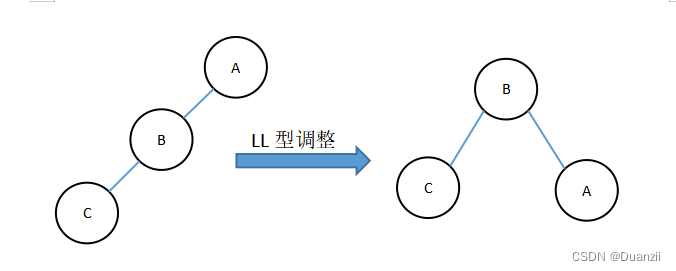

LL型调整的一般形式如下图所示，表示在A的左孩子B的左子树Bl(不一定为空)中插入节点而导致不平衡(子树的深度为h)。

这种情况调整如下：

（1）将A的左孩子B提升为新的根结点；

（2）将原来的根结点A降为B的右孩子；

（3）各子树按大小关系连接(Bl和Ar不变，Br调整为A的左子树)。

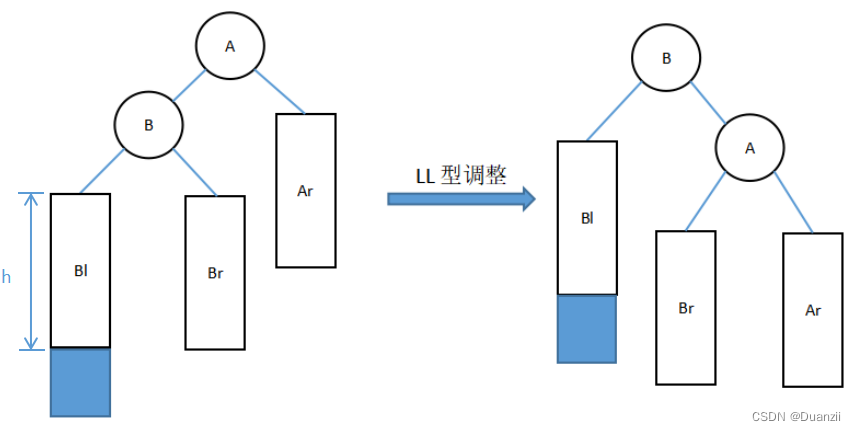
代码实现：

template<typename T>
AVLTreeNode<T>* AVLTree<T>::LeftLeftRotate(AVLTreeNode<T> *root) 
{
    AVLTreeNode<T> *lchild = root->left;//记录一下左子树根结点
    root->left = lchild->right;//将左子树的右子树变为根的左子树
    lchild->right = root;//将左子树的根变为整个树的根，然后让其右子树指向之前的根

    //更新一下当前子树的根结点的高height
    lchild->height = MaxHeight(lchild);
    //更新一下被旋下去的结点，即当前子树的根的右子树结点的高height
    root->height = MaxHeight(root);

    return lchild;//返回子树旋转后的新的根
}

AVLTreeNode* AVLTree::leftLeftRotate(AVLTreeNode* root)
{
    //root：失衡AVL树根节点
    AVLTreeNode* lchild = root->left;
    root->left = lchild->right;
    lchild->right = root;

    lchild->height = max(height(lchild->left), height(root)) + 1;
    root->height = max(height(root->left), height(root->right)) + 1;

    return lchild;//返回调整后的AVL树根节点
}

2. RR型调整（左旋）：

由于在A的右孩子的右子树上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由-1变为-2。

下图是RR型的最简单形式。显然按照大小关系，结点B应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡，A结点就好像是绕结点B逆时针旋转一样。

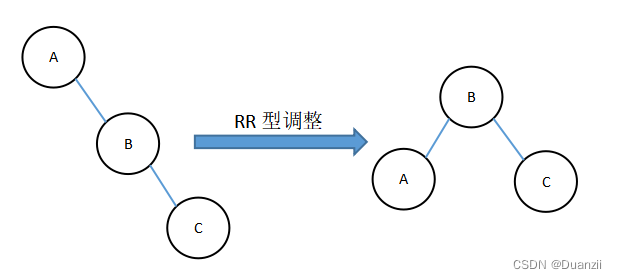
RR型调整的一般形式如下所示，表示在A的右孩子B的右子树Br中插入结点，而导致不平衡。这种情况调整如下：

（1）将A的右孩子B提升为新的根结点；
（2）将原来的根结点A降为B的左孩子；
（3）各子树按大小关系连接(AL和BR不变，BL调整为A的右子树)。

代码实现：

template<typename T>
AVLTreeNode<T>* AVLTreeTree<T>::RightRightRotate(AVLTreeNode<T> *root) 
{
    AVLTreeNode<T> *rchild = root->right;//记录一下右子树根结点
    root->right = rchild->left;//将右子树的左子树变为根的右子树
    rchild->left = root;//将右子树的根变为整个树的根，然后让其右子树指向之前的根
	//结点高度更新操作
    rchild->height = MaxHeight(rchild);
    root->height = MaxHeight(root);
	//返回新的根
    return rchild;
}

AVLTreeNode* AVLTree::rightRightRotate(AVLTreeNode* root)
{
    AVLTreeNode* rchild = root->right;
    root->right = rchild->left;
    rchild->left = root;
    rchild->height = max(height(root), height(rchild->right)) + 1;
    root->height = max(height(root->left), height(root->right)) + 1;

    return rchild;
}

3.LR型调整：

由于在A的左孩子的右子树上插入新节点，使原来平衡二叉树变得不平衡，此时A的平衡因子由1变为2。

下图是LR型的最简单形式。显然按照大小关系，节点C应作为新的根节点，其余两个节点分别作为左右孩子节点才能平衡。

LR型调整的一般形式如下图所示，表示在A的左孩子B的右子树(根结点为C)中插入结点，而导致不平衡。这种情况调整如下：

（1）将B的左孩子C提升为新的根结点；
（2）将原来的根结点A降为C的右孩子；
（3）各子树按大小关系连接(Bl和Ar不变，Cl和Cr分别调整为B的右子树和A的左子树)。

代码实现：

template<typename T>
AVLTreeNode<T>* AVLTreeTree<T>::LeftRightRotate(AVLTreeNode<T> *root) 
{
    root->left = RightRightRotate(root->left);//先对左子树进行进行RR旋转
    root = LeftLeftRotate(root);//然后对根节点进行LL旋转
    return root;//返回新的根
}

AVLTreeNode* AVLTree::leftRightRotate(AVLTreeNode* root)
{
    root->left = rightRightRotate(root->left); //先对左子树右右旋转
    return leftLeftRotate(root); //再对根节点左左旋转
}

4.RL型调整：

由于在A的右孩子的左子树上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由-1变为-2。

下图是RL型的最简单形式。显然按照大小关系，结点C应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡。

RL型调整的一般形式如下图所示，表示在A的右孩子B的左子树(根结点为C，不一定为空)中插入结点，而导致不平衡( h 表示子树的深度)。
这种情况调整如下：

（1）将B的左孩子C提升为新的根结点；
（2）将原来的根结点A降为C的左孩子；
（3）各子树按大小关系连接(AL和BR不变，CL和CR分别调整为A的右子树和B的左子树)。

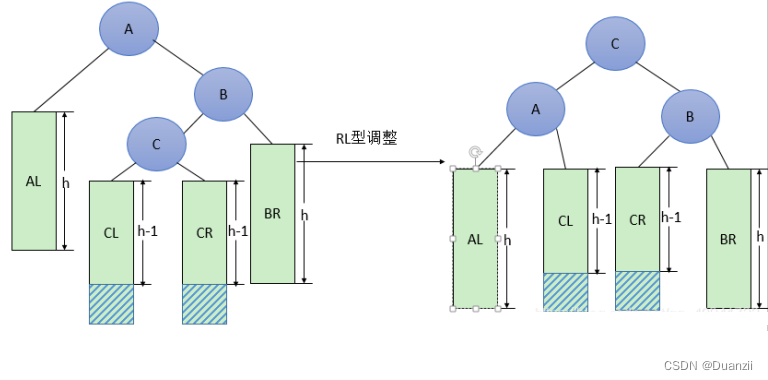
代码实现：

template<typename T>
AVLTreeNode<T>* AVLTree<T>::RightLeftRotate(AVLTreeNode<T> *root) 
{
    root->right = LeftLeftRotate(root->right);//先对右子树进行进行LL旋转
    root = RightRightRotate(root);//然后对根节点进行LL旋转
    return root;//返回新的根
}

AVLTreeNode* AVLTree::rightLeftRotate(AVLTreeNode* root)
{
    root->right = leftLeftRotate(root->right);
    return rightRightRotate(root);
}

五、AVL树的各种基本操作

1、查找节点

AVL树的查找与二叉查找树中的相同，因为AVL树总是保持平衡，并不会因为查找二改变结构，所以直接给出代码实现如下：

template<typename T>
AVLTreeNode<T>* AVLTreeTree<T>::ValueFind(AVLTreeNode<T> *root,T value) 
{
    //如果当前走到了空结点或者找到了value值的结点都会退出，前者说明找不到了，后者说明找到了
    while(root != NULL && root->key != value) 
    {
        if(root->key > value) 
        	root = root->left;//在左子树
        else 
        	root = root->right;//在右子树
    }
    return root;//没找到的话会返回NULL
}

void Search(int fg, AVLTree *node)
{
    if (node != NULL)
    {
        if (node->data == fg)
        {
            printf("查找值存在，值为%d\n", node->data);
        }
        else if (node->data > fg)
        {
            SearchData(fg, node->left); //递归查找左子树
        }
        else if (node->data < fg)
        {
            SearchData(fg, node->right); //递归查找右子树
        }
    }
    else if (node == NULL)
    {
        printf("查找值不存在\n");
    }
}

2.求最大（小）值节点

（1）最大值结点就是在树的最右边，也就是从根节点出发一直往右子树走，直到某个结点的右儿子为NULL 此时就找到了，代码如下：

template<typename T>
AVLTreeNode<T>* AVLTree<T>::MaxNode(AVLTreeNode<T> *root) 
{
    if(root == NULL) //特判一下空树的情况
        return NULL;
    if(root->right == NULL) //当结点的右子树为空，说明找到了
        return root;
    return MaxNode(root->right);//递归往右子树查找
}

最小值结点和最大值同理，从根节点出发一直往左子树走，直到某个节点的左儿子为 NULL，此时就找到了，代码如下：

template<typename T>
AVLTreeNode<T>* AVLTree<T>::MinNode(AVLTreeNode<T> *root) 
{
    if(root == NULL) 
        return NULL;//特判一下空树的情况
    if(root->left == NULL) //当结点的左子树为空，说明找到了
        return root;
    return MinNode(root->left);
}

3.插入节点（递归实现）

实现步骤如下图：

先来实现搜索最低失衡节点，从新插入的节点（叶子节点）往上搜索，就是说从新增结点开始向根部回溯，搜索到的第一个平衡因子>1（|左子树高度-右子树高度|>1）的节点，作为最低失衡节点，因为是从新插入的节点往上搜索，二叉树的搜索是单向的（结构体成员中只有左右子树），单独使用一个函数来实现逆向搜索实现起来并不方便，这里就把搜索最低失衡节点的操作放到递归实现的插入操作中。

template<typename T>
AVLTreeNode<T>* AVLTreeTree<T>::InsetNode(AVLTreeNode<T> *root,T value) 
{
    if(root == NULL) 
    {
        root = new AVLTreeNode<T>(value);
    } 
    else if(root->key > value) 
    {   //插入左子树
        root->left = InsetNode(root->left,value);
        if(Check_Balance(root->left,root->right)) 
        {   //插入左子树后发现失去平衡
            if(value < root->left->key) //因为插入结点左子树的左子树上，所以进行LL旋转
                root = LeftLeftRotate(root);
            else //插入结点在左子树的右子树上，所以LR旋转
                root = LeftRightRotate(root);
        }
    } 
    else 
    {   //插入右子树
        root->right = InsetNode(root->right,value);
        if(Check_Balance(root->right,root->left)) 
        {   //插入右子树后发现失去平衡
            if(value < root->right->key)//因为插入结点右子树的左子树上，所以进行RL旋转
                root = RightLeftRotate(root);
            else //因为插入结点右子树的右子树上，所以进行RR旋转
                root = RightRightRotate(root);
        }
    }
    root->height = MaxHeight(root);//计算结点高度
    return root;
}

AVLTree *AddNewNode(AVLTree *node, int NewData)
{
    AVLTree *p = NULL;

    if (node == NULL)
    {
        if ((node = (AVLTree *)malloc(sizeof(AVLTree))) == NULL)    //创建新节点
        {
            printf("内存不足");
            exit(0);
        }
        node->data = NewData;
        node->left = NULL;
        node->right = NULL;
        node->height = GetHeight(node);   
    }
    else if (NewData > node->data)    
    {
        node->right = AddNewNode(node->right, NewData);
        node->height = GetHeight(node);
        if (GetHeight(node->right) - GetHeight(node->left) > 1)    //右子树高度 - 左子树高度
        {
            exit(0);
        }
        return node;
    }
    else if (NewData < node->data)
    {
        node->left = AddNewNode(node->left, NewData);
        node->height = GetHeight(node);
        if (GetHeight(node->left) - GetHeight(node->right)  > 1)    //左子树高度 - 右子树高度
        {
            exit(0);
        }
        return node;
    }
    else if (NewData == node->data)
    {
        printf("不允许插入重复值");
        exit(0);
    } 
    return node;
}

用下图简单解释一下插入流程：

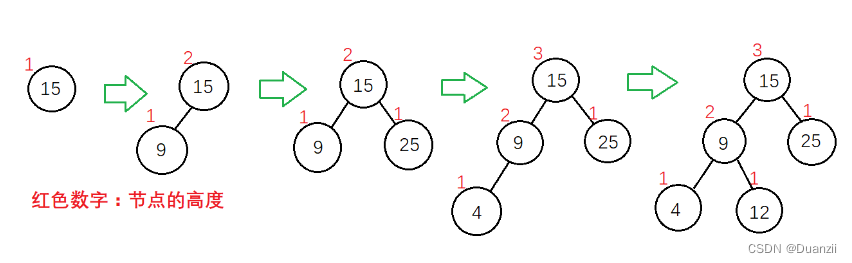
4.删除节点

删除节点比插入节点的操作稍微复杂一点，因为插入时，进行一次平衡处理（一次平衡处理可能包含多次旋转），整棵树都会处于平衡状态，而在删除时，需要进行多次平衡处理，才能保证树处于平衡状态。

AVL树的删除操作前半部分和二叉查找树相同，只不过删除后要检查树是否失去平衡，如果失衡就需要重新调整平衡，并更新节点高度，总的来说可以分为以下几种情况：

（1）删除叶子节点：

*删除后二叉树没有失去平衡

*删除后二叉树失去平衡

上图的RE型失衡只有在删除操作时才可能出现，在插入时不可能出现，RE型失衡的旋转方式和RR型失衡的旋转方式是一模一样。虽然删除节点时遇到的失衡情况多了两种：LE和RE ，但是旋转的方式依旧是那四种LL、RR、LR、RL。

AVLTree *DeletNode(AVLTree *node, int DelData)
{
     AVLTree *SNode = NULL; //后继节点
     AVLTree *PSNode = NULL;  //后继节点的父节点
     AVLTree *tr = NULL; //临时保存待释放节点的子树，避免free后找不到左右子树
  
     if (node == NULL)
     {
         printf("删除节点不存在");
         exit(0);
     }
     else if (DelData > node->data)
     {
         node->right = DeletNode(node->right, DelData);
         
         if (GetHeight(node->left) - GetHeight(node->right) > 1)
         {
             temp = nod->left;
 
             if (GetHeight(temp->left) >= GetHeight(temp->right)) //LL型或LE型失衡、两种情况处理方式相同
             {
                 node = LL_Rotation(node);
             }
             else//LR型失衡
             {
                 node = LR_Rotation(node);
             }
         }
 
         node->height = GetHeight(node); //更新节点高度
     }
     else if (DelData < node->data)
     {
         node->left = DeletNode(node->left, DelData);
 
         if (GetHeight(node->right) - GetHeight(node->left) > 1)
         {
             tr = node->right;
 
             if (GetHeight(tr->right) >= GetHeight(tr->left))    //RR或RE型失衡、两种情况处理方式相同
             {
                 node = RR_Rotation(node);
             }
             else    //RL型失衡
             {
                 node = RL_Rotation(node);
             }
         }
 
         node->height = GetHeight(node); //更新节点高度
     }
     else if (DelData == node->data)
     {
         if (node->right == NULL && node->left == NULL) //若待删除节点为叶子节点
         {
             free(node);
             return NULL;    
         }
     }

（2）删除带有一个子节点的节点

若是只有左子树，那么让其左子树根节点继承当前位置，然后删除该节点
若是只有右子树，那么让其右子树根节点继承当前位置，然后删除该节点

     else if (DelData == node->data)
     {
          if (node->right == NULL && node->left == NULL) //若待删除节点为叶子节点
          {
              free(node);
              return NULL;    
          }
          else if (node->right == NULL && node->left != NULL) //若待删除节点只有左子树
          {
              temp = node->left;
              free(node);
              return temp;
          }
          else if (node->right != NULL && node->left == NULL) //若待删除节点只有右子树
          {
              temp = node->right;
              free(node);
              return temp;
          }
     }

（3）删除带有两个子节点的节点

若左子树比右子树高（分为三步进行）：
- ①找到当前节点的左子树的最大值节点（前驱）
- ②将这个左子树的最大值赋给当前的根节点
- ③删除左子树的最大值的节点
若右子树比左子树高（分为三步进行）：
- ①找到当前结点的右子树上的最小值节点（后继）
- ②将这个右子树的最小值赋给当前的根节点
- ③删除右子树的最小值节点

删除带有两个子节点的节点时，需要找到待删除的节点的后继节点或者前驱节点。需要注意的是，删除节点时不会出现“后继节点不是删除节点的子节点，且后继节点有右子树”这种情况，如下图：

图中14节点已经失衡了，在插入的时候就会被调整，所以不会出现“后继节点不是删除节点的子节点，且后继节点有右子树”这种情况。

     else //若待删除节点既有左子树也有右子树
     {
         SNode = SearchSuccessorNode(nod->right); //搜索后继节点
         PSNode = SearchParentofSNode(nod->right, nod->right); //搜索后继节点的父节点
         if (nod->right == SNode)    //后继节点为待删除节点的右子树（后继节点有右子树和没有右子树的操作相同）
         {
             SNode->left = nod->left;
             free(nod);
 
             return SNode;
         }
         else if (nod->right != SNode && SNode->right == NULL) //后继节点不为待删除节点的右子树，并且该后继节点没有右子树
         {
             SNode->left = nod->left;
             SNode->right = nod->right;
             PSNode->left = NULL;

             free(nod);
             return SNode;
         }
         else if (nod->right != SNode && SNode->right != NULL)    //后继节点不为待删除节点的右子树，并且该后继节点有右子树
         {     
             PSNode->left = SNode->right;    //后继节点的右子树作为后继节点父节点的左子树
             SNode->left = nod->left;
             SNode->right = nod->right;

             free(nod);
             return SNode;
         }
     }
 }

template<typename T>
AVLTreeNode<T>* AVLTreeTree<T>::DeleteNode(AVLTreeNode<T> *root, AVLTreeNode<T> *node) {
    if(root == NULL) return NULL;
    if(root->key == node->key) 
    {   //找到了删除的结点
        if(root->left != NULL && root->right != NULL) 
        {
            //如果删除的结点的左树和右子树都不为空
            if(GetHeight(root->left) > GetHeight(root->right)) 
            {
                //如果左子树比右子树高的话，分三步进行

                //找到当前结点的左子树的最大值结点
                AVLTreeNode<T> *max_node = MaxNode(root->left);

                //将这个左子树的最大值赋给当前的根节点
                root->key = max_node->key;

                //删除左子树的最大值的结点（因为这个结点一定是只有左子树或者没有左子树的情况）
                root->left = DeleteNode(root->left,max_node);
            } 
            else 
            {
                //右子树和左子树更高或者相等,同样分三步

                //找到当前结点的右子树上的最小值结点
                AVLTreeNode<T> *min_node = MinNode(root->right);

                //将这个右子树的最小值赋给当前的根节点
                root->key = min_node->key;

                //删除右子树的最小值结点（和上面同理，一定是一个只有右子树或者没有右子树的情况）
                root->right = DeleteNode(root->right,min_node);
            }
        } 
        else 
        {   //左右子树都为空，或者是左子树为空，或者是右子树为空
            AVLTreeNode<T> *tmp = root;//记录下删除的结点
            if(root->left == NULL) //如果左子树为空，那么就由右子树继承（当然右子树也可能是一个空树）
                root = root->right;
            else //否则左子树继承
                root = root->left;
            delete tmp;
        }
    }
    else if(root->key > node->key) 
    {   //删除的结点在左节点
        root->left = DeleteNode(root->left,node);
        if(Check_Balance(root->right,root->left)) 
        {   //右子树可能会失衡
            AVLTreeNode<T> *TempRightNode = root->right;
            if(GetHeight(TempRightNode->left) > GetHeight(TempRightNode->right))
                root = RightLeftRotate(root);//RR旋
            else
                root = RightRightRotate(root);//RL旋
        }
    } 
    else 
    {   //删除的结点在右子树
        root->right = DeleteNode(root->right,node);
        if(Check_Balance(root->left,root->right)) 
        {   //左子树可能会发生失衡
            AVLTreeNode<T> *TempLeftNode = root->left;
            if(GetHeight(TempLeftNode->left) > GetHeight(TempLeftNode->right))
                root = LeftLeftRotate(root);//LL旋
            else
                root = LeftRightRotate(root);//LR旋
        }
    }
    if(root)
        root->height = MaxHeight(root);
    return root;
}